门控循环单元GRU与长短期记忆网络LSTM

本文主要是介绍门控循环单元GRU与长短期记忆网络LSTM，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

门控循环单元与长短期记忆网络

门控隐状态

问题提出：对于一个序列来说不是每个观察值都是同等重要想只记住相关的观察需要：

• 能关注的机制（更新门）
• 能遗忘的机制（重置门）

第一个词元的影响至关重要。 我们希望有某些机制能够在一个记忆元里存储重要的早期信息。 如果没有这样的机制，我们将不得不给这个观测值指定一个非常大的梯度， 因为它会影响所有后续的观测值。

重置门和更新门

首先介绍重置门（reset gate）和更新门（update gate）。 我们把它们设计成(0,1)区间中的向量， 这样我们就可以进行凸组合。 重置门允许我们控制“可能还想记住”的过去状态的数量； 更新门将允许我们控制新状态中有多少个是旧状态的副本。

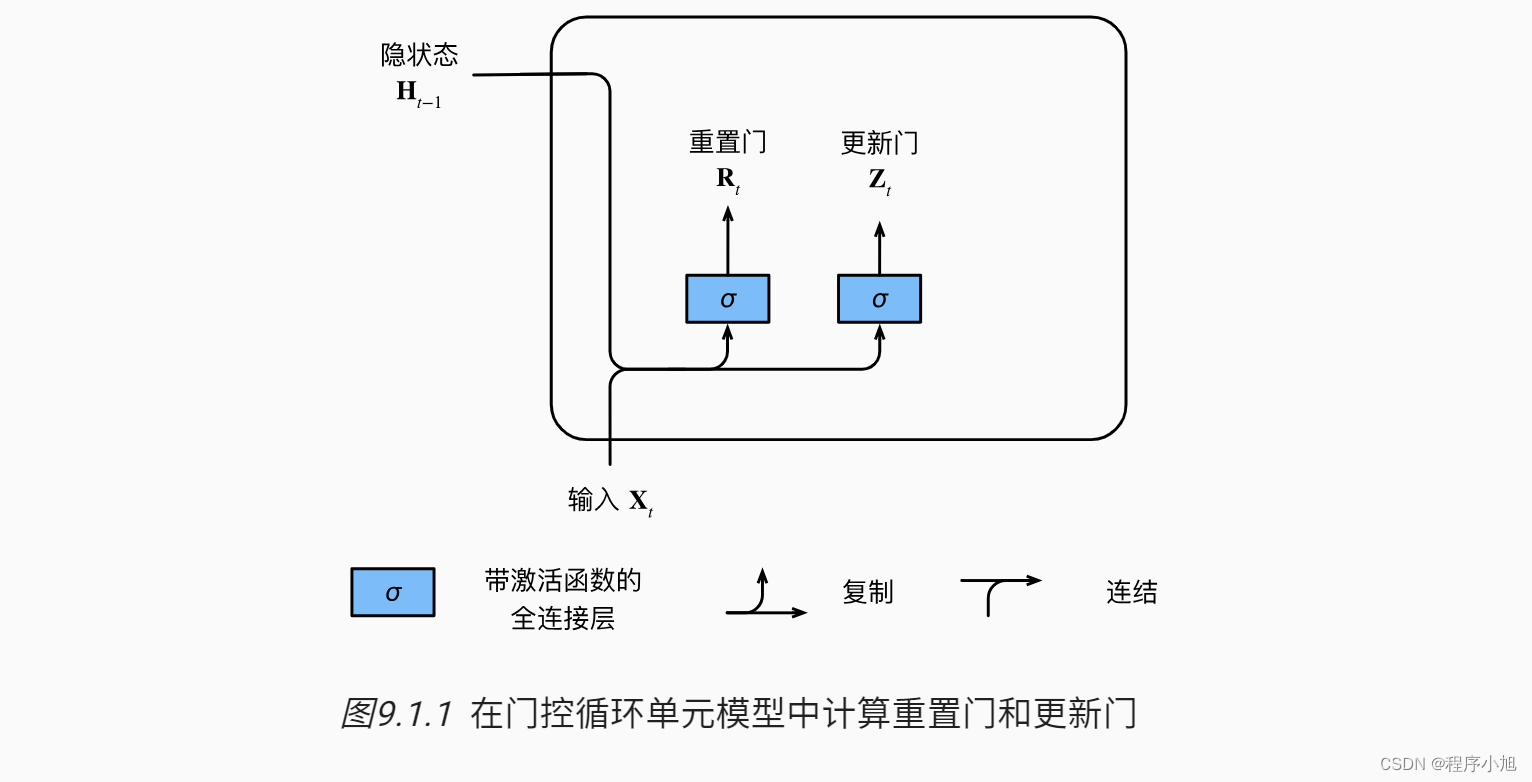
首先引出重置门与更新门的计算步骤：
$$\begin{array}{rl}{\mathbf{R}}_t& =\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xr}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hr}+{\mathbf{b}}_r\right)\\ {\mathbf{Z}}_t& =\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xz}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hz}+{\mathbf{b}}_z\right)\end{array}$$

候选隐状态

让我们将重置门Rt 与
$${\mathbf{H}}_t=\varphi \left({\mathbf{X}}_t{\mathbf{W}}_{xh}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}+{\mathbf{b}}_h\right).$$
中的常规隐状态更新机制集成， 得到在时间步t的候选隐状态（candidate hidden state）

$${\tilde{\mathbf{H}}}_t=\tanh \left({\mathbf{X}}_t{\mathbf{W}}_{xh}+\left({\mathbf{R}}_t\odot {\mathbf{H}}_{t-1}\right){\mathbf{W}}_{hh}+{\mathbf{b}}_h\right),$$

我们使用tanh非线性激活函数来确保候选隐状态中的值保持在区间(-1,1)中。

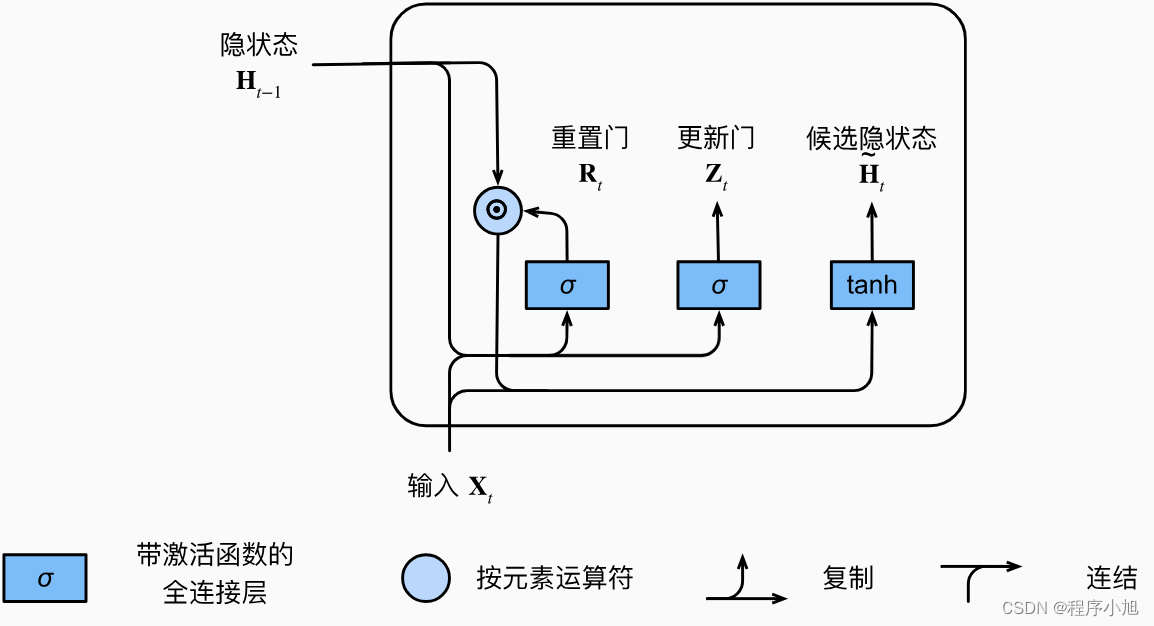
之后说明候选隐状态的分析：

每当重置门Rt中的项接近1时， 我们恢复了普通的循环神经网络。 对于重置门Rt中所有接近0的项， 候选隐状态是以Xt作为输入的多层感知机的结果。 因此，任何预先存在的隐状态都会被重置为默认值。

注意其中引入的sigmoid函数信息

隐状态

上述的计算结果只是候选隐状态，我们仍然需要结合更新门Zt的效果。 这一步确定新的隐状态Ht。

在多大程度上来自旧的状态Ht-1和 新的候选状态Ht~ 。 更新门Zt仅需要在 Ht-1和Ht~ 之间进行按元素的凸组合就可以实现这个目标。 这就得出了门控循环单元的最终更新公式：

$${\mathbf{H}}_t={\mathbf{Z}}_t\odot {\mathbf{H}}_{t-1}+\left(1-{\mathbf{Z}}_t\right)\odot {\tilde{\mathbf{H}}}_t.$$

每当更新门Zt接近1时，模型就倾向只保留旧状态。 此时，来自
的Xt信息基本上被忽略， 从而有效地跳过了依赖。 相反，当
Zt接近0时， 新的隐状态就会接近候选隐状态Ht~

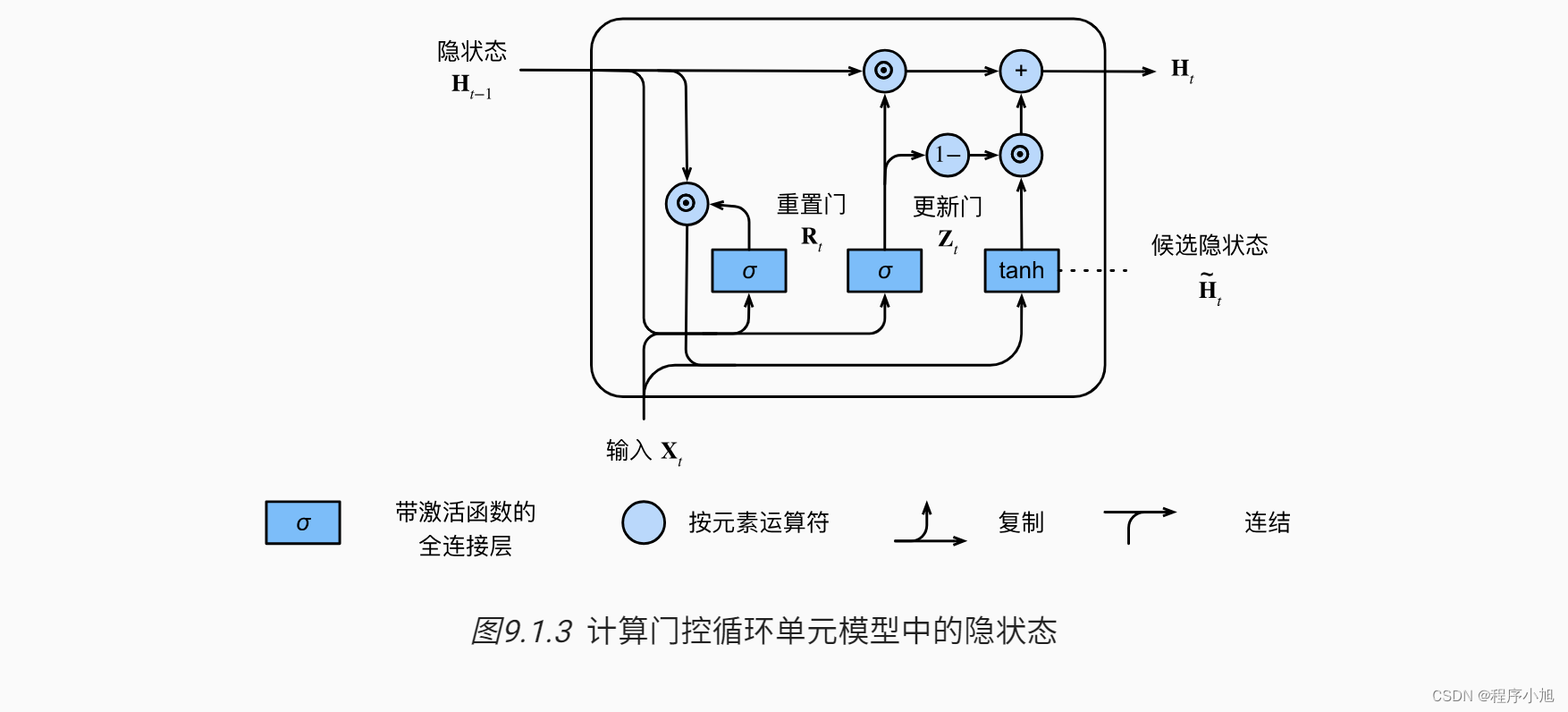
• 重置门有助于捕获序列中的短期依赖关系；

• 更新门有助于捕获序列中的长期依赖关系。

GRU的简单实现

import torch
from torch import nn
from d2l import torch as d2lbatch_size, num_steps = 32, 35

train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
#%%
def get_params(vocab_size, num_hiddens, device):num_inputs = num_outputs = vocab_sizedef normal(shape):return torch.randn(size=shape, device=device)*0.01def three():return (normal((num_inputs, num_hiddens)),normal((num_hiddens, num_hiddens)),torch.zeros(num_hiddens, device=device))W_xz, W_hz, b_z = three()  # 更新门参数W_xr, W_hr, b_r = three()  # 重置门参数W_xh, W_hh, b_h = three()  # 候选隐状态参数# 输出层参数W_hq = normal((num_hiddens, num_outputs))b_q = torch.zeros(num_outputs, device=device)# 附加梯度params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]for param in params:param.requires_grad_(True)return params

def init_gru_state(batch_size, num_hiddens, device):return (torch.zeros((batch_size, num_hiddens), device=device), )
#%%
def gru(inputs, state, params):W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = paramsH, = stateoutputs = []for X in inputs:Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)H = Z * H + (1 - Z) * H_tildaY = H @ W_hq + b_qoutputs.append(Y)return torch.cat(outputs, dim=0), (H,)

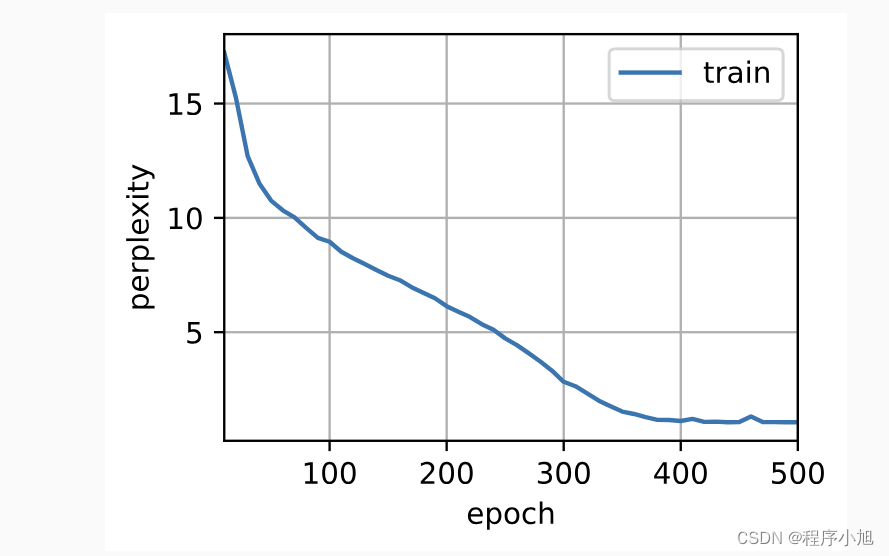
进行模型的训练

vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,init_gru_state, gru)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

长短期记忆网络

长期以来，隐变量模型存在着长期信息保存和短期输入缺失的问题。 解决这一问题的最早方法之一是长短期存储器（long short-term memory，LSTM）

门控记忆元

长短期记忆网络引入了记忆元（memory cell），或简称为单元（cell）。 有些文献认为记忆元是隐状态的一种特殊类型， 它们与隐状态具有相同的形状，其设计目的是用于记录附加的信息。 为了控制记忆元，我们需要许多门。 其中一个门用来从单元中输出条目，我们将其称为输出门（output gate）。 另外一个门用来决定何时将数据读入单元，我们将其称为输入门（input gate）。 我们还需要一种机制来重置单元的内容，由遗忘门（forget gate）来管理， 这种设计的动机与门控循环单元相同，

• 输出门
• 输入门
• 遗忘门

输入门、遗忘门和输出门

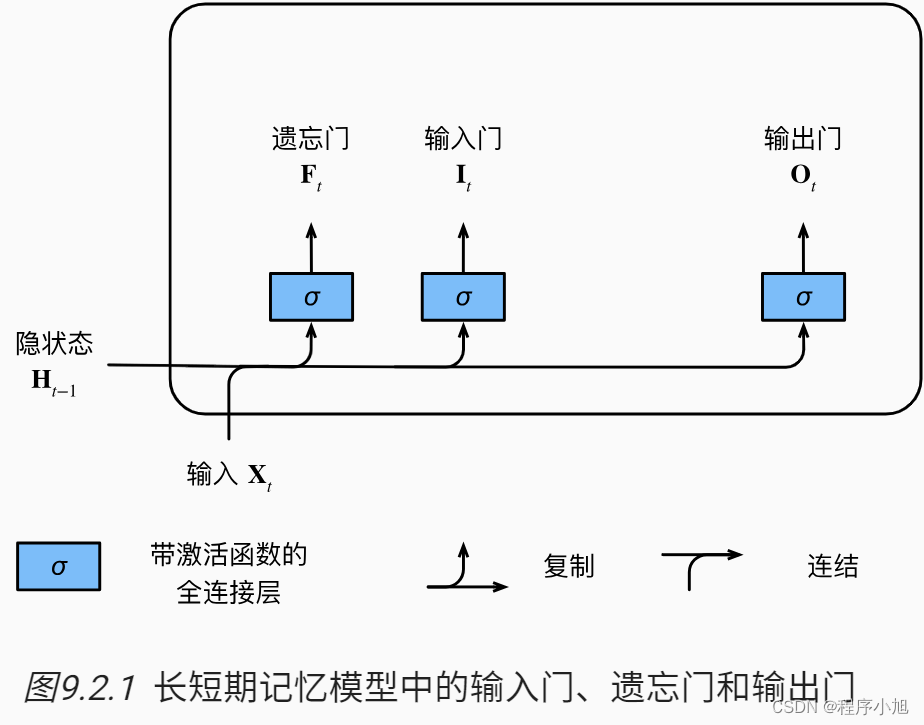
$$\begin{array}{rl}{\mathbf{I}}_t& =\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xi}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hi}+{\mathbf{b}}_i\right)\\ {\mathbf{F}}_t& =\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xf}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hf}+{\mathbf{b}}_f\right),\\ {\mathbf{O}}_t& =\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xo}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{ho}+{\mathbf{b}}_o\right)\end{array}$$

候选记忆元

由于还没有指定各种门的操作，所以先介绍候选记忆元（candidate memory cell） 。 它的计算与上面描述的三个门的计算类似， 但是使用tanh函数作为激活函数，函数的值范围为（-1,1）下面导出在时间步t处的方程：

$${\tilde{\mathbf{C}}}_t=\tanh \left({\mathbf{X}}_t{\mathbf{W}}_{xc}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hc}+{\mathbf{b}}_c\right)$$

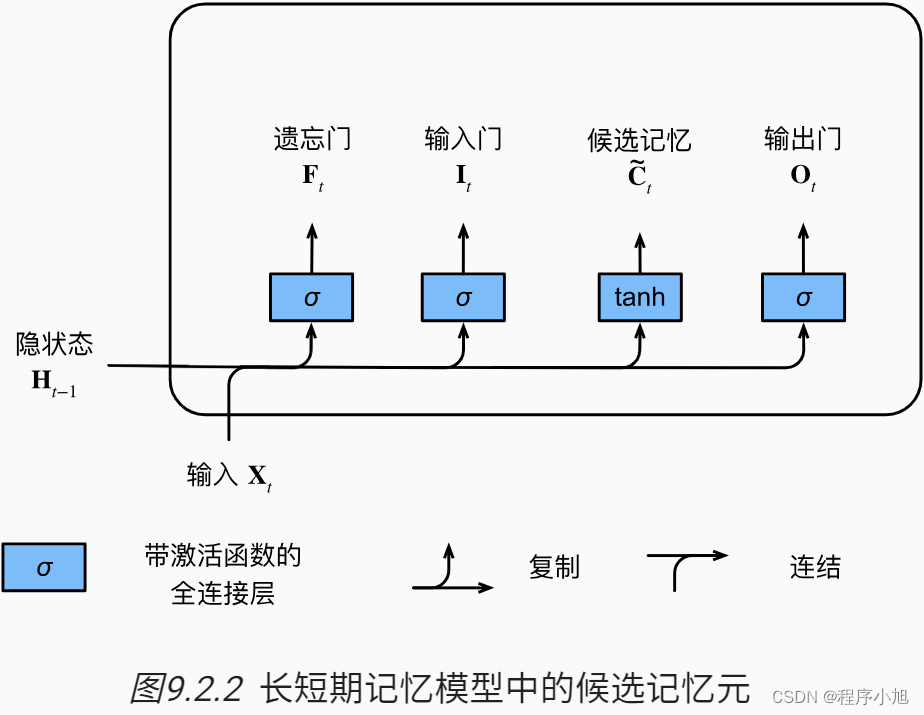
记忆元

在门控循环单元中，有一种机制来控制输入和遗忘（或跳过）。类似地，在长短期记忆网络中，也有两个门用于这样的目的：输入门It控制采用多少来自Ct的新数据，而遗忘门Ft控制保留多少过去的记忆元Ct-1∈ Rn×h的内容。使用按元素乘法，得出

$${\mathbf{C}}_t={\mathbf{F}}_t\odot {\mathbf{C}}_{t-1}+{\mathbf{I}}_t\odot {\tilde{\mathbf{C}}}_t.$$

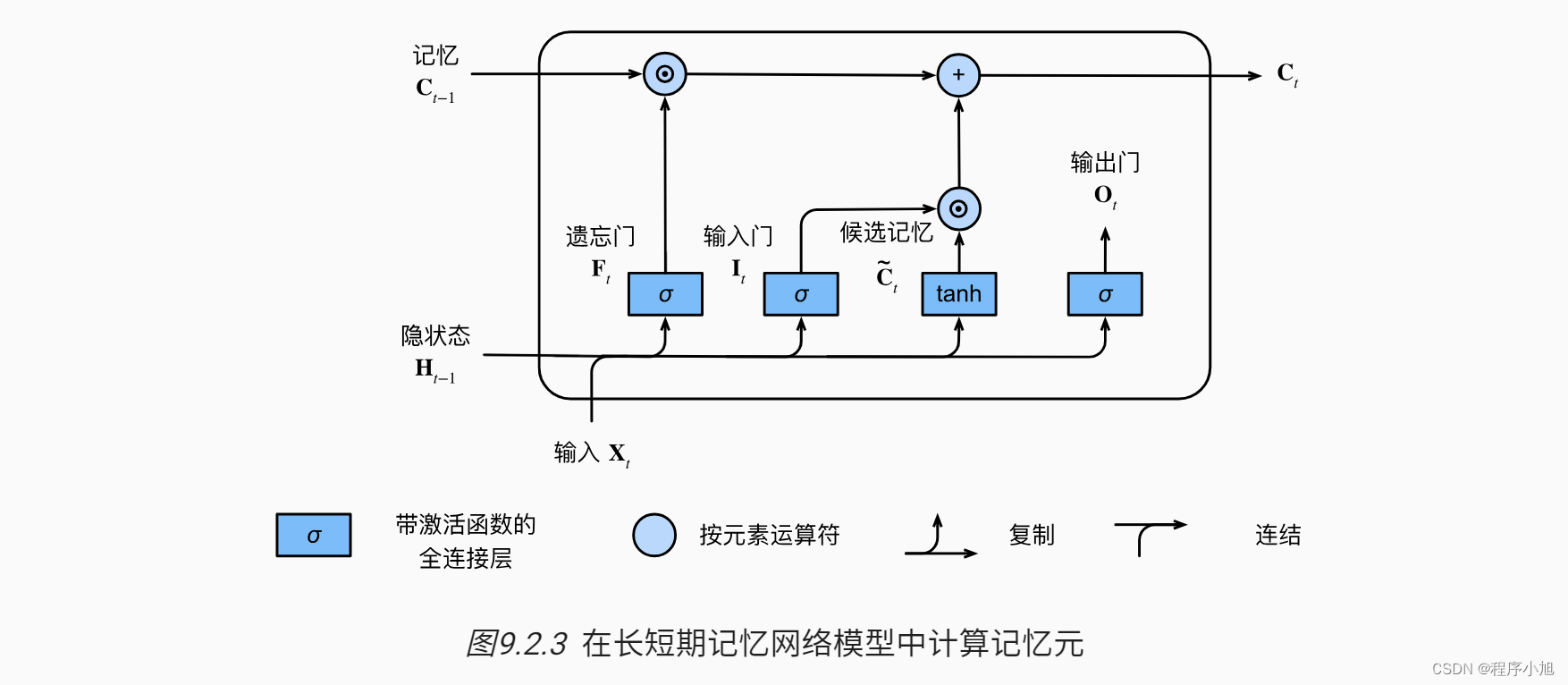
如果遗忘门始终为1且输入门始终为0，则过去的记忆元Ct-1将随时间被保存并传递到当前时间步。引入这种设计是为了缓解梯度消失问题，并更好地捕获序列中的长距离依赖关系。

隐状态

$${\mathbf{H}}_t={\mathbf{O}}_t\odot \tanh \left({\mathbf{C}}_t\right).$$

最后将输出门中的信息与记忆元中经过激活函数得到的信息进行运算就可以得到最后输出的隐状态。

只要输出门接近1，我们就能够有效地将所有记忆信息传递给预测部分， 而对于输出门接近0，我们只保留记忆元内的所有信息，而不需要更新隐状态。

LSTM简单实现

import torch
from torch import nn
from d2l import torch as d2lbatch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

初始化模型的参数

def get_lstm_params(vocab_size, num_hiddens, device):num_inputs = num_outputs = vocab_sizedef normal(shape):return torch.randn(size=shape, device=device)*0.01def three():return (normal((num_inputs, num_hiddens)),normal((num_hiddens, num_hiddens)),torch.zeros(num_hiddens, device=device))W_xi, W_hi, b_i = three()  # 输入门参数W_xf, W_hf, b_f = three()  # 遗忘门参数W_xo, W_ho, b_o = three()  # 输出门参数W_xc, W_hc, b_c = three()  # 候选记忆元参数# 输出层参数W_hq = normal((num_hiddens, num_outputs))b_q = torch.zeros(num_outputs, device=device)# 附加梯度params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,b_c, W_hq, b_q]for param in params:param.requires_grad_(True)return params

搭建网络结构

def init_lstm_state(batch_size, num_hiddens, device):return (torch.zeros((batch_size, num_hiddens), device=device),torch.zeros((batch_size, num_hiddens), device=device))

实际模型的定义与我们前面讨论的一样： 提供三个门和一个额外的记忆元。 请注意，只有隐状态才会传递到输出层， 而记忆元不直接参与输出计算。

def lstm(inputs, state, params):[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,W_hq, b_q] = params(H, C) = stateoutputs = []for X in inputs:I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)C = F * C + I * C_tildaH = O * torch.tanh(C)Y = (H @ W_hq) + b_qoutputs.append(Y)return torch.cat(outputs, dim=0), (H, C)

训练预测得到最后的结果：

vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

这篇关于门控循环单元GRU与长短期记忆网络LSTM的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---