本文主要是介绍【博士每天一篇文献-算法】Progressive Neural Networks,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
阅读时间:2023-12-12
1 介绍
年份:2016
作者:Andrei A. Rusu,Neil Rabinowitz,Guillaume Desjardins,DeepMind 研究科学家,也都是EWC(Overcoming catastrophic forgetting in neural networks)算法的共同作者。
期刊: 未录用,发表于arXiv
引用量:2791
代码:https://github.com/TomVeniat/ProgressiveNeuralNetworks.pytorch
Rusu A A, Rabinowitz N C, Desjardins G, et al. Progressive neural networks[J]. arXiv preprint arXiv:1606.04671, 2016.
提出了一种深度强化学习架构——渐进式网络(progressive networks),它通过保留一系列预训练模型并在训练过程中学习这些模型之间的侧向连接(lateral connections),从而实现跨任务的知识迁移。既能利用迁移学习的优势,又能避免灾难性遗忘的问题。在Atari游戏和3D迷宫游戏上进行了强化学习评估实验,通过平均扰动敏感性(Average Perturbation Sensitivity, APS)和平均Fisher敏感性(Average Fisher Sensitivity, AFS)两种方法,分析了在不同层次上迁移发生的情况。
2 创新点
提出了一种新的神经网络架构——渐进式网络(progressive networks),它通过保留一系列预训练模型并在训练过程中学习这些模型之间的侧向连接(lateral connections),从而实现跨任务的知识迁移。
在多种强化学习任务(包括Atari游戏和3D迷宫游戏)上广泛评估了这种架构,并展示了它在性能上超越了基于预训练和微调(pretraining and finetuning)的常见基线方法。
开发了一种基于Fisher信息和扰动分析的新颖分析方法,能够详细分析跨任务迁移在哪些特征和哪些层次上发生。
3 相关研究
灵感启发来源:Terekhov A V, Montone G, O’Regan J K. Knowledge transfer in deep block-modular neural networks[C]//Biomimetic and Biohybrid Systems: 4th International Conference, Living Machines 2015, Barcelona, Spain, July 28-31, 2015, Proceedings 4. Springer International Publishing, 2015: 268-279.【模块化网络,引用量82】
4 算法
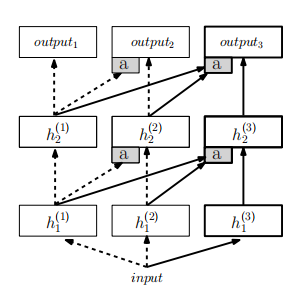
- 模型初始化:渐进式网络从一个单列的深度神经网络开始,该网络经过训练直到收敛。这第一列网络包含了多个层次,每层有特定的隐藏单元和参数。
- 任务切换:当引入新任务时,先前任务的网络参数被“冻结”,即不再更新。然后,为新任务实例化一个具有新参数的新列网络,这些参数是随机初始化的。
- 侧向连接:新任务的网络列通过侧向连接接收来自之前所有列的输入。这些连接允许新任务利用先前任务学习到的特征。
- 网络架构:每个新任务的网络列都包含一个前馈的深度神经网络,其中每层都接收来自前一层以及所有先前列的侧向输入。
- 非线性激活:在所有中间层使用ReLU激活函数(( f(x) = \max(0, x) ))。
- 适配器(Adapters):为了改善初始条件和执行降维,在侧向连接中引入了非线性适配器。适配器通常是一个单隐藏层的多层感知器(MLP),用于调整不同输入的尺度并执行投影。
- 参数更新:在训练新任务时,只有新列的参数会被更新,而先前列的参数保持不变,从而避免了灾难性遗忘。
- 多任务学习:渐进式网络的目标是在训练结束时能够独立解决所有任务,并通过迁移学习加速新任务的学习。
- 容量管理:随着任务数量的增加,网络的参数数量也会增加。论文提出可以通过修剪或在线压缩等方法来控制参数的增长。
- 实验评估:论文通过在强化学习领域的实验来评估渐进式网络的性能,包括在Atari游戏和3D迷宫游戏中的表现。
5 实验分析
5.1 实验设置
(1)定义了两个指标量化神经网络在迁移学习过程中特征的重用程度和迁移效果。
**平均Fisher敏感性(AFS)**是量化特征的重要性。AFS通过计算Fisher信息矩阵的对角元素来量化网络策略对每一层特定特征微小变化的敏感性。这有助于识别哪些特征对网络的输出有较大的影响。AFS还可以用来分析在不同任务之间迁移时,哪些特征被新任务所利用。这有助于理解迁移学习的效果和机制。此外,通过在不同层级上计算AFS,研究者可以了解在网络的哪个层次上发生了有效的迁移,是低级感官特征还是高级控制特征。
**平均扰动敏感性(APS)**是直观的特征贡献评估。APS通过在网络的特定层注入高斯噪声,并观察这种扰动对性能的影响,来评估源任务特征对目标任务的贡献。如果性能显著下降,则表明该特征对最终预测非常重要。APS提供了一种直观的方法来观察迁移特征的有效性。通过扰动分析,可以识别出在迁移过程中哪些特征是有益的,哪些可能是有害的。
(2)网络构建过程
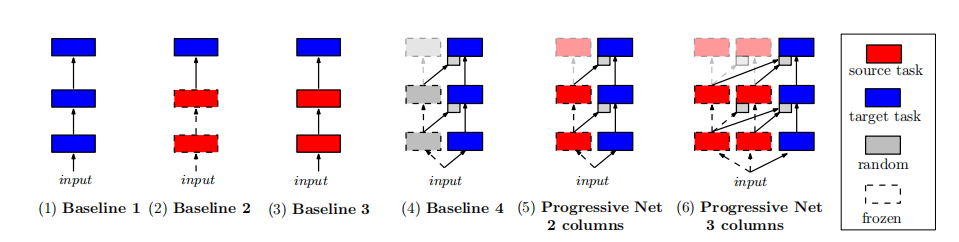
展示了如何通过添加更多的列来逐步构建网络,每个新列都建立在之前学习的任务之上。
5.2 在Pong Soup迁移任务的性能分析
(1)迁移任务效果
“Pong Soup” 实验是为了研究在不同变体的 Pong 游戏中,神经网络如何迁移在原始 Pong 游戏中学到的知识。实验使用了多个经过修改的 Pong 游戏版本,这些变体在视觉和控制层面上有所不同,包括:
- Noisy:在输入图像上添加了高斯噪声。
- Black:背景变为黑色。
- White:背景变为白色。
- Zoom:输入图像被放大并平移。
- V-flip、H-flip 和 VH-flip:输入图像在垂直或水平方向上翻转。
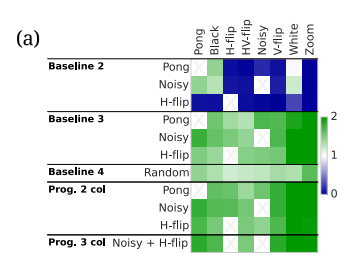
热图展示了不同Pong变体之间迁移学习的效果。颜色的深浅表示迁移得分,得分越高,颜色越深。迁移得分是相对于基线1的性能提升或下降来计算的。得分大于1表示性能提升,小于1表示性能下降。迁移矩阵中的每个单元格对应于一个源任务到目标任务的迁移情况。行代表源任务,列代表目标任务。Baseline2(单列,仅输出层微调)中蓝色区域较多,说明这种方法未能学习目标任务,导致负面迁移。Baseline3(单列,全网络微调)这种方法显示出较高的正面迁移,说明在源任务和目标任务之间存在一定程度的相似性,允许网络通过微调大部分参数来学习新任务。PNN网络在中位数和平均分数上都优于基线3,表明渐进式网络在利用迁移学习方面更为有效。特别是,渐进式网络能够更好地利用先前任务的知识来加速新任务的学习,并且对于兼容性较好的源任务和目标任务,迁移效果更加明显。
(2)不同网络层的特征敏感性分析
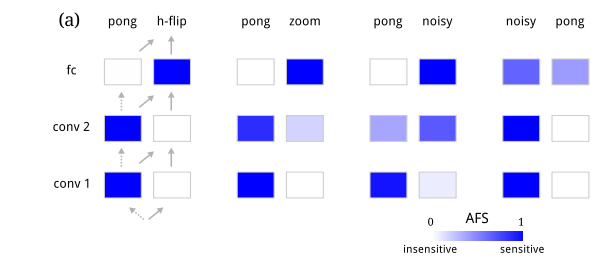
颜色越深表示该列在该层对输出的影响越大,即网络对该特征的依赖性越高。在Pong的不同变体之间迁移时,网络倾向于重用相同的低级视觉特征,特别是那些对于检测球和球拍位置至关重要的特征。尽管一些低级特征被重用,但网络也需要学习新的中级视觉特征来适应任务的变化,如在Zoom变体中所见。通过AFS分析,论文展示了渐进式网络如何在不同层级上有效地迁移和调整特征,以提高在新任务上的性能。
5.3 Atari目标游戏的迁移任务分析
(1)Fisher敏感性分析
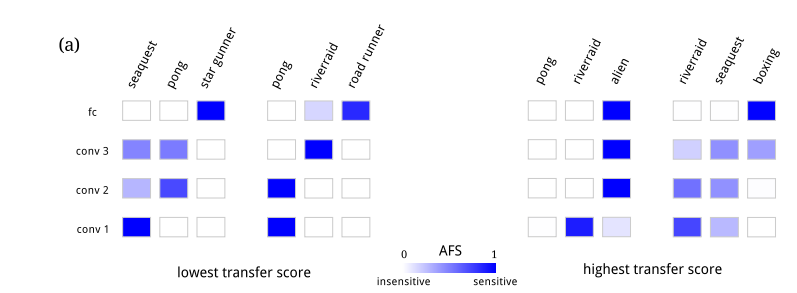
图中说明如果网络过度依赖旧特征而未能学习新特征,可能导致迁移效果不佳。
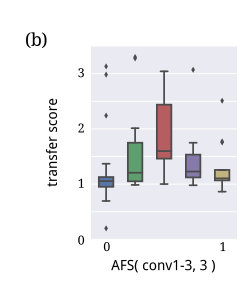
展示了平均AFS值与迁移得分之间的关系,正迁移可能发生在对源任务特征的依赖与对目标任务新特征学习的平衡之间。这表明在新任务上学习新特征对于成功的迁移至关重要。
总之,通过Fisher敏感性分析,论文发现在某些情况下,渐进式网络在新任务上既重用了先前任务的特征,又学习了新的特征,这有助于实现更好的迁移效果。
5.4 3D迷宫游戏的迁移任务性能分析
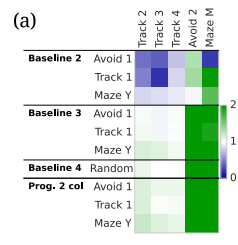
即使在简单游戏中,PNN网络也能通过学习新的视觉特征来提高性能,这些特征对于识别不同任务中变化的奖励物品很重要。
6 思考
(1)论文的算法过程和模型比较简单,但是其中的适应器(Adapter)是什么作用?具体是怎么实现的?在代码中如何体现?
适配器通过在侧向连接中引入非线性,帮助网络更好地初始化新任务的学习,从而加速收敛。
还用于执行降维操作。这是因为随着网络逐渐增加新列来学习新任务,输入特征的维度也在增长。适配器通过减少特征维度,帮助网络更有效地处理这些高维输入。
适配器的设计确保了随着网络逐渐增加新列,由于侧向连接产生的参数数量与原始网络参数的数量级相同,从而控制了模型的参数增长。
这篇关于【博士每天一篇文献-算法】Progressive Neural Networks的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








