本文主要是介绍群体优化算法---水波优化算法介绍以及应用于聚类数据挖掘代码示例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
介绍
水波优化算法(Water Wave Optimization, WWO)是一种新兴的群智能优化算法,灵感来自水波在自然环境中的传播和衰减现象。该算法模拟了水波在水面上传播和碰撞的行为,通过这些行为来寻找问题的最优解。WWO算法由三种主要的操作组成:波浪传播、波浪碰撞和波浪衰减
主要操作
波浪传播(Wave Propagation):
每个个体在搜索空间中产生新的候选解,类似于波浪的传播过程。
传播过程中,每个新解的生成依赖于当前解的位置和一定的随机扰动。
波浪碰撞(Wave Collision):
当波浪传播到一定程度时,会发生碰撞,产生新的波浪。
这些新的波浪代表了新的候选解,通常会在局部搜索范围内进行调整和优化。
波浪衰减(Wave Attenuation):
波浪传播和碰撞会逐渐减弱,类似于能量的耗散过程。
这一过程可以帮助算法避免过早收敛到局部最优解,并增强全局搜索能力
算法步骤
初始化:
随机生成初始种群,每个个体代表一个候选解。
计算每个个体的适应度值。
迭代过程:
波浪传播:对每个个体,根据其当前位置和随机扰动产生新的候选解,并计算新解的适应度。
波浪碰撞:对选定的个体进行局部搜索,通过生成新的解来提高搜索效率。
波浪衰减:逐步减少波浪的能量,以增加算法的稳定性和收敛性。
终止条件:
迭代达到最大次数或满足其他收敛条件时,算法终止。
返回找到的最优解及其适应度值。
水波优化算法的优势
全局搜索能力强:通过波浪传播和碰撞机制,能够有效跳出局部最优解,增强全局搜索能力。
简单易实现:算法结构简单,参数较少,容易实现和应用。
适应性强:可应用于连续和离散优化问题,并在不同领域展示出良好的性能
应用领域
函数优化:WWO算法可用于求解复杂的多峰函数的全局最优解。
工程优化:在结构优化、参数调优等工程问题中表现出色。
数据挖掘:用于分类、聚类等数据挖掘任务,展示出良好的适应性
本文实例
我们将使用次算法进行聚类数据挖掘,我们需要对数据集进行聚类分析。这包括使用WWO算法来优化聚类中心的位置,从而最大化聚类效果
代码
WWOClustering.m
function [best_centers, best_fitness, cluster_assignments] = WWOClustering(data, num_clusters, num_iterations, num_individuals, bounds)[num_points, dim] = size(data);% 初始化种群population = bounds(1) + (bounds(2) - bounds(1)) * rand(num_individuals, num_clusters, dim);fitness = zeros(num_individuals, 1);for i = 1:num_individualsfitness(i) = evaluateFitness(squeeze(population(i, :, :)), data, num_clusters);end% 记录最优解[best_fitness, best_idx] = min(fitness);best_centers = squeeze(population(best_idx, :, :));for iter = 1:num_iterations% 波浪传播for i = 1:num_individualsnew_solution = population(i, :, :) + randn(1, num_clusters, dim) * (bounds(2) - bounds(1)) / iter;new_solution = min(max(new_solution, bounds(1)), bounds(2)); % 确保新解在边界内new_fitness = evaluateFitness(squeeze(new_solution), data, num_clusters);if new_fitness < fitness(i)population(i, :, :) = new_solution;fitness(i) = new_fitness;endend% 波浪碰撞for i = 1:num_individualsif rand < 0.1 % 10%的概率进行碰撞操作collision_partner = randi(num_individuals);new_solution = (population(i, :, :) + population(collision_partner, :, :)) / 2;new_fitness = evaluateFitness(squeeze(new_solution), data, num_clusters);if new_fitness < fitness(i)population(i, :, :) = new_solution;fitness(i) = new_fitness;endendend% 记录当前最优解[current_best_fitness, best_idx] = min(fitness);if current_best_fitness < best_fitnessbest_fitness = current_best_fitness;best_centers = squeeze(population(best_idx, :, :));endend% 计算最终的聚类分配cluster_assignments = assignClusters(data, best_centers, num_clusters);
endfunction fitness = evaluateFitness(centers, data, num_clusters)[num_points, dim] = size(data);fitness = 0;for i = 1:num_pointsmin_dist = inf;for j = 1:num_clustersdist = norm(data(i, :) - centers(j, :));if dist < min_distmin_dist = dist;endendfitness = fitness + min_dist;end
endfunction assignments = assignClusters(data, centers, num_clusters)[num_points, dim] = size(data);assignments = zeros(num_points, 1);for i = 1:num_pointsmin_dist = inf;for j = 1:num_clustersdist = norm(data(i, :) - centers(j, :));if dist < min_distmin_dist = dist;assignments(i) = j;endendend
end
runWWOClustering.m
data = rand(100, 2); % 随机生成数据点
num_clusters = 3; % 聚类数目
num_iterations = 100; % 迭代次数
num_individuals = 50; % 种群数量
bounds = [0, 1]; % 搜索空间[best_centers, best_fitness, cluster_assignments] = WWOClustering(data, num_clusters, num_iterations, num_individuals, bounds);
disp('最佳聚类中心:');
disp(best_centers);
disp('最佳适应度值:');
disp(best_fitness);% 绘制聚类结果
figure;
hold on;
colors = ['r', 'g', 'b', 'c', 'm', 'y'];
for i = 1:num_clustersscatter(data(cluster_assignments == i, 1), data(cluster_assignments == i, 2), 36, colors(i), 'filled');
end
scatter(best_centers(:, 1), best_centers(:, 2), 100, 'k', 'x');
title('WWO Clustering Result');
xlabel('X');
ylabel('Y');
hold off;
说明
1.WWOClustering:主函数,用于执行WWO聚类算法。
初始化种群:在给定的边界范围内随机生成初始种群。
波浪传播:根据当前解的位置和随机扰动产生新解。
波浪碰撞:选定个体进行局部搜索,通过生成新解来提高搜索效率。
记录最优解:在每次迭代中记录当前最优解。
计算最终的聚类分配:根据最优聚类中心计算最终的聚类分配。
2.evaluateFitness:计算适应度值,衡量聚类中心对数据点的聚类效果。
计算距离:计算每个数据点到最近聚类中心的距离,并累加所有距离作为适应度值。
3.assignClusters:根据聚类中心对数据点进行聚类分配。
分配聚类:计算每个数据点到各个聚类中心的距离,并分配到最近的聚类中心。
4.示例使用:随机生成数据点,执行WWO聚类算法,并显示结果。
绘制聚类结果:使用scatter函数绘制聚类结果,并标记聚类中心。
效果
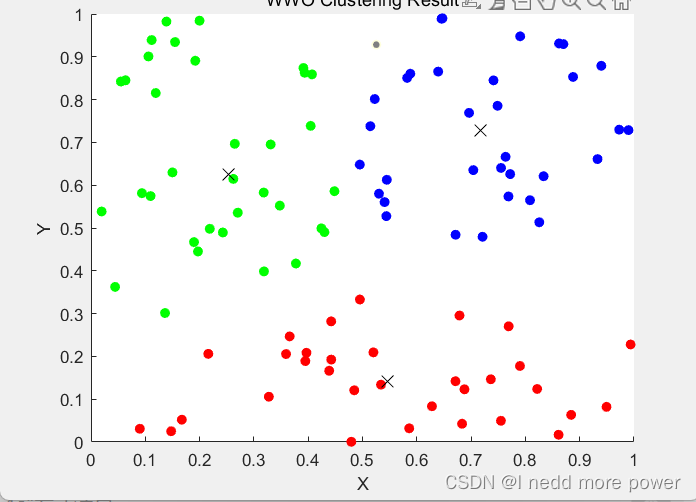

这篇关于群体优化算法---水波优化算法介绍以及应用于聚类数据挖掘代码示例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







