本文主要是介绍Mamba v2诞生:2 那些烧脑的矩阵们,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大模型技术论文不断,每个月总会新增上千篇。本专栏精选论文重点解读,主题还是围绕着行业实践和工程量产。若在某个环节出现卡点,可以回到大模型必备腔调或者LLM背后的基础模型新阅读。而最新科技(Mamba,xLSTM,KAN)则提供了大模型领域最新技术跟踪。若对于具身智能感兴趣的请移步具身智能专栏。技术宅麻烦死磕AI架构设计。
Mamba的出现为带来了全新的思路和可能性,通过对结构化半可分离矩阵的各种分解方法的理论研究,可以将状态空间模型SSM与注意力机制Attention的变种进行紧密关联,进而提出一种状态空间对偶SSD的理论框架。
状态空间对偶使得研究人员设计一种新的架构 (Mamba-2),其核心层是对 Mamba(选择性SSM)进行改进,速度提高了2-8倍,同时在语言建模方面能够保持对Transformers的压力。

Mamba的矩阵表达式
上一篇介绍了Mamba的概览,先来温习下Mamba-1模型公式:
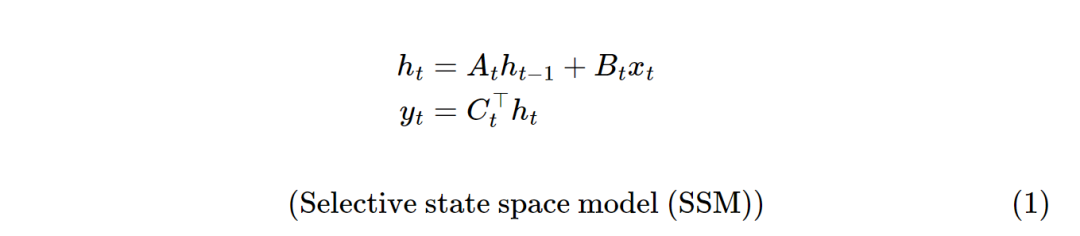
其中xt为t时刻的输入,yt为t时刻的输出。定义的 𝑥∈𝑅𝑇→𝑦∈𝑅𝑇映射。将 𝑥𝑡和𝑦𝑡视为标量,将隐藏状态ℎ𝑡视为𝑁长的一维向量,其中𝑁是一个独立的超参数,称为状态大小、状态维数或状态扩展因子。
选择性状态空间模型SSM(Mamba-1)允许 (𝐴,𝐵,𝐶)矩阵参数随时间变化,这里张量 𝐶的形状为𝐶∈𝑅(𝑇,𝑁),张量A的形状为𝐴∈𝑅(𝑇,𝑁,𝑁),张量B的形状为B∈𝑅(𝑇,𝑁)。
那么将输入和输出扩展为序列,则可以得到下式:
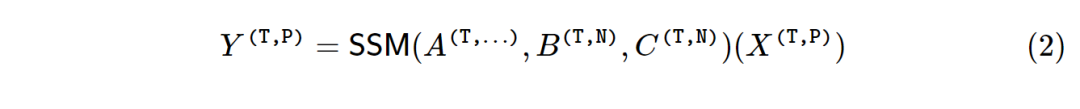
将序列模型改写为矩阵变换,则提供了理解模型结构和特征的强大工具。一般的非线性RNN(如LSTM)不能写成矩阵表达式,但状态空间模型可以。事实上,只要展开SSM递归的定义,SSM第(2)式就可以写成矩阵变化格式:

其中Mij可以定义为:

各位读者,A的上标乘号代表连乘,而下边则代表着从i到j。下图为推导过程,不喜就跳过吧。

在mamba-2中因为Ai这个矩阵的设计方式是对角线元素的取值都相同为ai,其余的元素为0。所以将A抽出来,则可以得到:

这个时候将1,2,4的式子放在一起已经包含式子3:

其中L为:

推导过程就不展开了,但是可以看看下面的例子:x,y均为T维的向量,x乘以一个下图的下三角矩阵,则等同于右侧的公式。<要好好推敲一下!>

许多序列模型明确地被激励或定义为矩阵序列变换—最显著的是 Transformers,其中的注意力矩阵。另一方面,RNN和SSM以前没有采用矩阵的模式来表达。通过提供SSM的显式矩阵变换形式就打开新的大门。从计算的角度来看,任何计算状态空间模型前向传递的方法都可以看作是半可分矩阵上的矩阵乘法算法。

半可分矩阵
Semiseparable Matrices
若是下三角部分(即对角线上或对角线下)中包含的每个子矩阵的秩最多为 N,则 (下三角) 矩阵𝑀 是 N-Semiseparable Matrices。
这里将 N 称为半可分矩阵的阶或秩。半可分矩阵有许多结构化表示,包括分层半可分 (HSS)、顺序半可分 (SSS) 和 Bruhat 形式 。在Mamba-2中主要使用SSS形式。
若一个下三角矩M∈𝑅(𝑇,𝑇)可以写为如下的格式:

则它一定会有一个N-SSS的表现形式。而一个N-SSS的矩阵M(4)一定可以表示为如下,

这个方程将广泛的被使用于Mamba-2的快速算法推导。
那来看看1-Semiseparable Matrices的特殊情况,Mamba-2的矩阵A也是标量,那么这个时候:

而

SSD模型的对偶性可以看作是半可分离矩阵上的两种不同的矩阵乘法算法。这时其实SSM就是一个半可分矩阵的转换。

其中M根据(5)可以进行如下的变换:
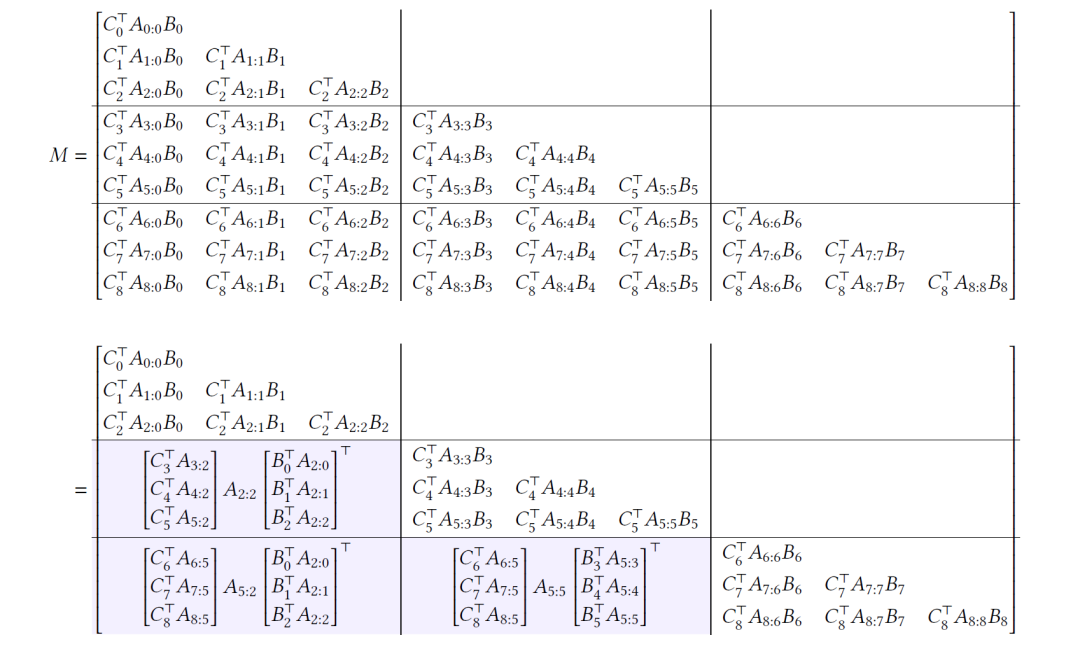
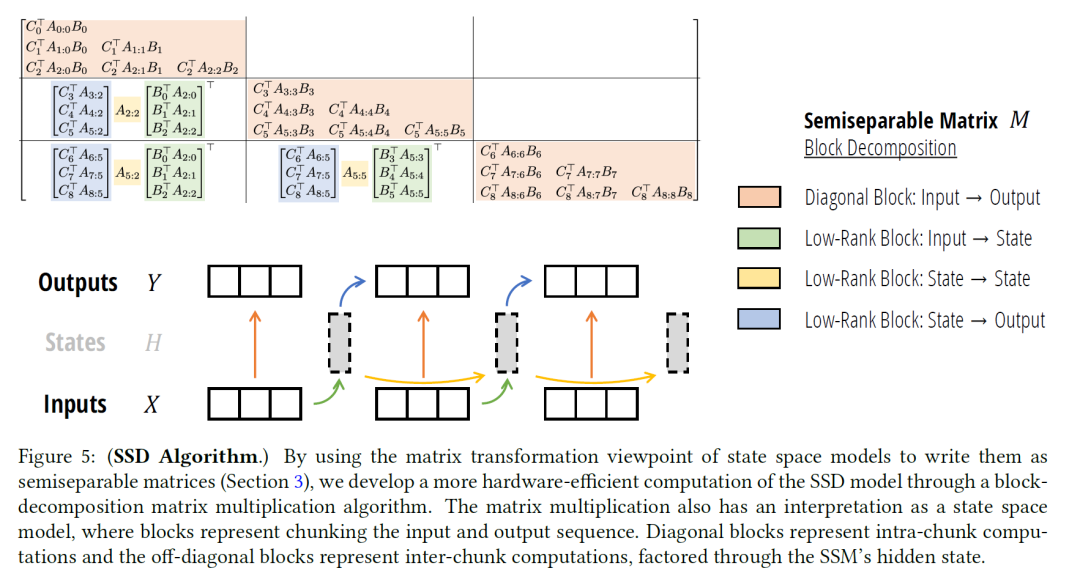
将矩阵切分之后,可以将这些矩阵块分为四种颜色。
-
橙色:每个对角线块都是一个较小的半可分离矩阵,可以随意计算
-
绿色:只有T/Q 完全不同的绿色块,中间有很多是共享,可以使用批处理 matmul计算
-
黄色:黄色项本身形成一个1-半可分离矩阵,可以使用SSM扫描
-
蓝色:与绿色类似,这些可以使用批处理 matmul 进行计算
其实这些分解刚好可以很巧妙的构造出分块和状态传递(下图中间部分)。一切都可以切块,然后能加速的加速,能用SSM扫描的扫描,最终将输出并行算出结果。
半可分矩阵为状态空间对偶 (SSD) 提供了全新的视角,其中对偶模式分别指线性时间半可分矩阵乘法算法和二次时间朴素矩阵乘法。
线性形式是一种结构化的矩阵乘法算法,它利用半可分离矩阵的结构按顺序计算输出 。二次形式是实现完整矩阵的朴素矩阵乘法算法。
SSD也提出了一种更通用的混合算法,可以看作是结合了线性和二次形式,最终获得美妙的结果。这种利用半可分离矩阵的块分解,进而推导出一种新的矩阵乘法算法让人耳目一新!
若存在有点恍惚,请移步“Mamba”温习功课!
这篇关于Mamba v2诞生:2 那些烧脑的矩阵们的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




