【计算机图形学】DINA: Deformable INteraction Analogy

本文主要是介绍【计算机图形学】DINA: Deformable INteraction Analogy，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 做的事

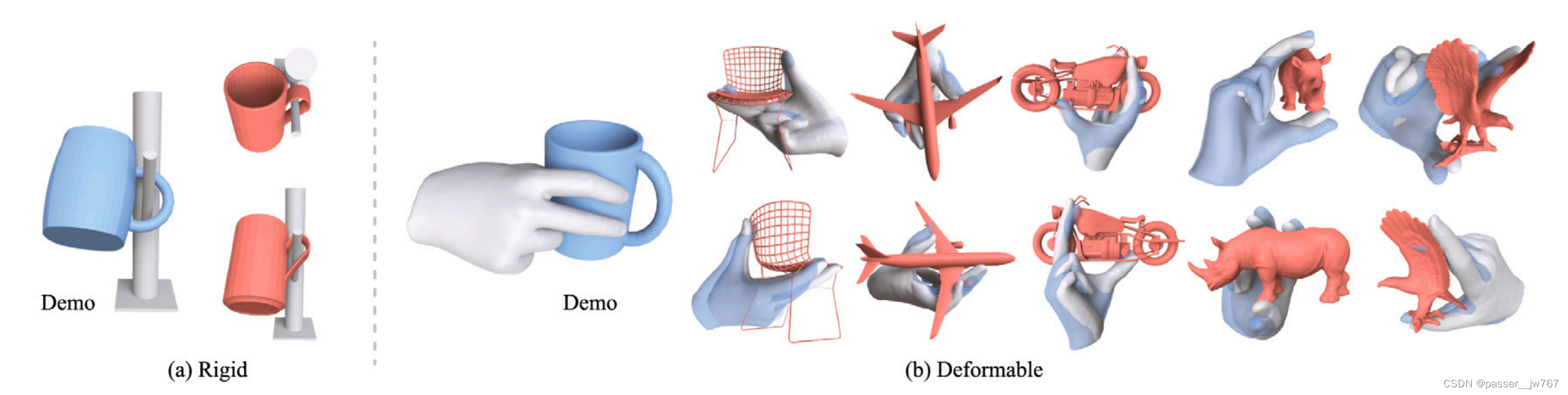
引入“可变形交互模仿”的定义，该定义为：在两个3D物体之间生成相近的交互。给定一个锚定物体（如手）和源物体（如被手握着的马克杯）的交互示例，我们的目标是在相同的锚定物体和多样化的新目标物体（如玩具飞机）之间生成更多3D交互。这个锚定物体可以是rigid的也可以是deformable的

实际上这也就是优化锚定物体的pose或shape，在模仿演示的情况下适应新的目标物体。

为了实现这种优化，该文章致力于使用交互接口（Interaction Interface，ITF），由在锚定物体上的一组点定义，这是一种描述性和鲁棒的交互表示，易于进行非刚性变形。在使用ITF的交互之间建模二者的相似性，以引导锚定对象通过变形与新物体上的ITF匹配。

2. 为什么做

数据驱动的3D交互生成模型通常需要大量的数据进行训练，这种不需要大量数据就能够生成交互的方法有益于丰富数据并生成更多样化的结果

3. 介绍

要解决这个问题，最基础的问题是：

1. 如何表示和优化3D交互；

2. 如何测量目标交互和示例交互的相似性；

3. 最重要的是要找到一种符合下列要求的表示方法：

• 对物体-物体的交互敏感，而不是只对单个3D物体

• 对于交互物体的形状变化鲁棒的表示

• 适合于非刚性与适应性变化，例如人类的手具有较高的维度

• 能用于可变形的建模

基于上述要求，研究了一种比IBS还要好用的ITF，称为交互接口。这种交互接口被定义为锚定物体上的一组固定点。

为了评估示例交互与目标交互的相似性，这里基于逐点距离，来表示物体-物体的交互，逐点距离是从锚定物体上的交互接口到源物体的距离。给定一个示例交互和任意姿态的（可能被旋转之类的）新的目标物体，本文的优化将分为两个步骤：

1. 执行刚性交互类比，通过距离特征匹配，让锚定物体刚性地变化到合适的位置

2. 根据上述结果，局部变形ITF，以及锚定物体，使得结果的point-wise ditance特征（锚定手与物体两两之间的距离）与示例交互中的尽可能接近

4. 方法

4.1 问题定义

给定交互示例$(O_a,O_s)$，其中$O_a$是能够变形的锚点物体，$O_s$是源物体，将来会被替换成以随机姿态给定的目标物体$O_T$。目标是优化：

{ T ‾ , D ‾ } = arg min ⁡ { T , D } d i s t ( f ( O a , O s ) , f ( T ⋅ D ( O a ) , O t ) ) \{\overline{T},\overline{D}\}=\argmin_{\{T,D\}} dist(f(O_a, O_s), f(T·D(O_a), O_t)) {T,D}=argmin{T,D}​dist(f(Oa​,Os​),f(T⋅D(Oa​),Ot​))

其中$f(O_1,O_2)$是物体$O_1$和$O_2$之间的交互表示，$dist(f_1,f_2)$是在两个交互表示之间定义的距离度量。

4.2 交互表示

为了表示示例交互$(O_a,O_s)$，利用了交互二分面（Interaction Bisector Surface，IBS），这种方式对于表示交互物体的局部几何细节在空间上的关系是非常鲁棒的。想要提取IBS，首先要在两个交互物体（在本文就是锚定物体和源物体间）上均匀采样一组点，然后为这两个物体计算Voronoi图。IBS是Voronoi图ridges的一个子集，接着构成了表面网格。但IBS计算本身很复杂，对应的距离测量方式也很难使得IBS应用于DINA中。

为了真正确定交互发生的区域，进一步在$O_a$上选择一组点，通过IBS构成交互接口ITF，表示为$卡{方}_a$。相比IBS，这是一种从交互物体中分离的表示，ITF是在锚定物体$O_a$上的一组点。因此，锚定物体的变形可以自然地由ITF驱动，对于点$p\in 卡{方}_a$，记录到源物体的最短距离$O_s$为：$d(p,O_s)={\min }_{q\in O_s}||p-q|{|}_2$。

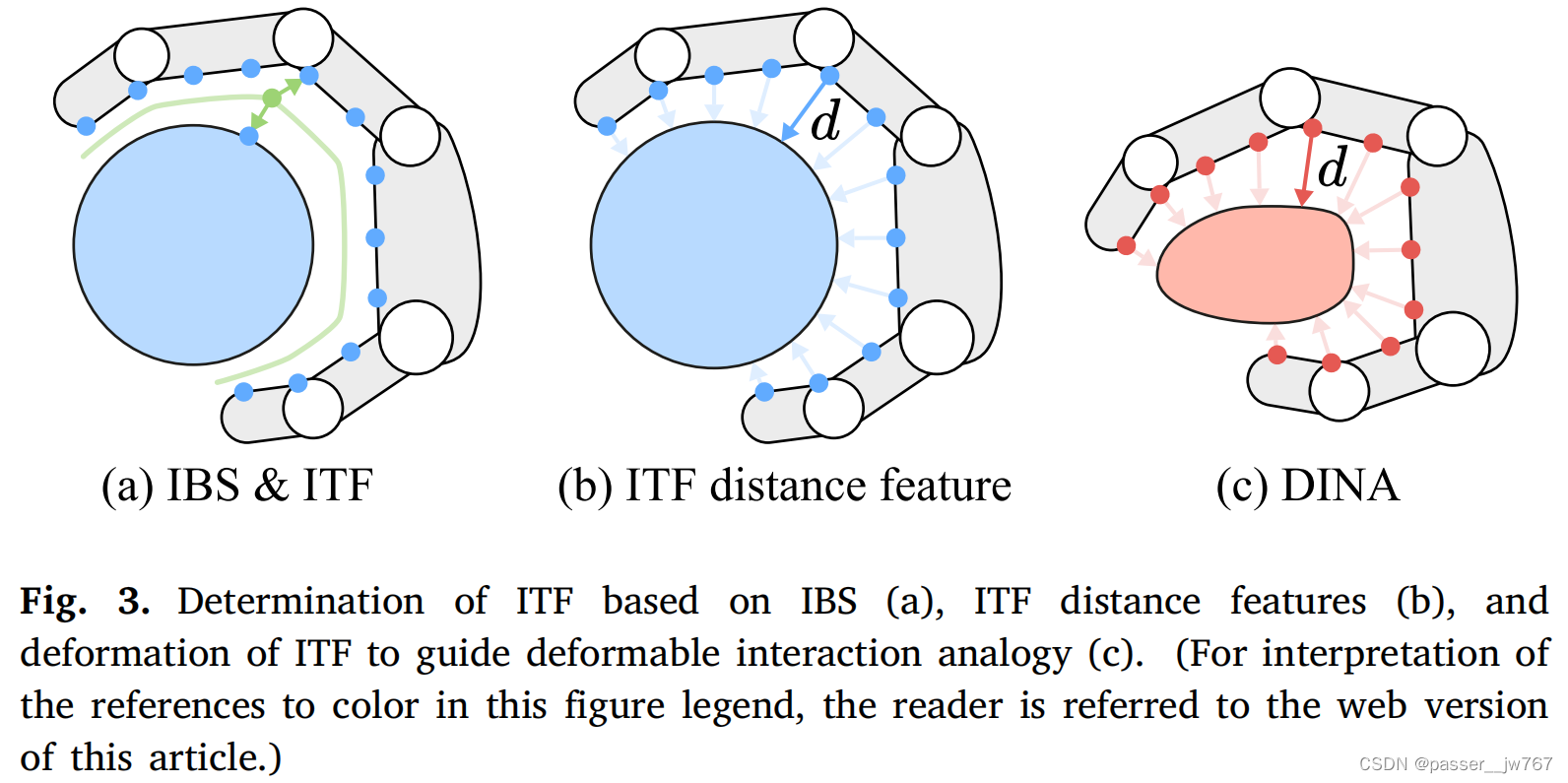
如图所示，(a)展示的就是交互二分面，这是位于交互主体与交互客体之间的一个二分面，将交互区域均匀地分成两部分。(b)是作者计算的所谓的ITF交互接口，就是在交互主体上取一组点，计算这组点到物体的最近距离。©是在目标物体上使用交互接口计算的与目标物体之间的距离，是deform后交互接口的直观展示。

4.3 交互类比

目标函数。 由上表示，实际上优化目标是目标物体的逐点距离 { d ( T ⋅ D ( p ) , O t } \{d(T·D(p),O_t\} {d(T⋅D(p),Ot​}，使得它尽可能地接近$d(p,O_s)$，也就是让上图的(b)和©的距离尽可能接近。ITF是交互主体$O_a$上的一组点$卡{方}_a$，所以目标函数可以被视作：

$L_{ITF}(T,D)={\sum }_{p\in 卡{方}_a}|d(p,O_s)-d(T\cdot D(p),O_t)|$

就是使两个距离尽可能接近，套一个绝对值

为了避免严重自交问题，进一步加上了一个显式惩罚项：

$L_{PEN}(T,D)={\sum }_{x_i\in O_a^{\prime }}\max ((x_i-x_t)\cdot n_t,0)+\lambda {\sum }_{x_j\in O_t^{\prime }}\max ((x_j-x_a)\cdot n_a,0)$

这里的$O_a^{\prime }=T\cdot D(O_a)$是transfrom和变形后的锚定物体，$x_t$是$O_t$上具有法线$n_t$最近点$x_i$，$x_a$是$O_a^{\prime }$上的具有法线$n_a$的最近点$x_j$。

法线恒为正方向，就是约束不自交吧，先约束物体表面上的点，再约束锚点物体的点。

最后的目标函数就是上面两个损失的结合。

4.4 从刚性到可变形的优化

目标物体的$O_t$的大小和几何可能和源物体$O_s$有着较大的差异，锚点物体可能和源物体$O_s$的交互看起来很自然很好，但不一定适应于$O_t$。因此不仅需要对锚点物体$O_a$变形，还需要做transform，以更好地适应目标物体$O_t$。

一种最直观的方法就是同时优化global transform $T$和local deformation $D$，但是这样搜索空间太大，很容易陷入局部最小值。

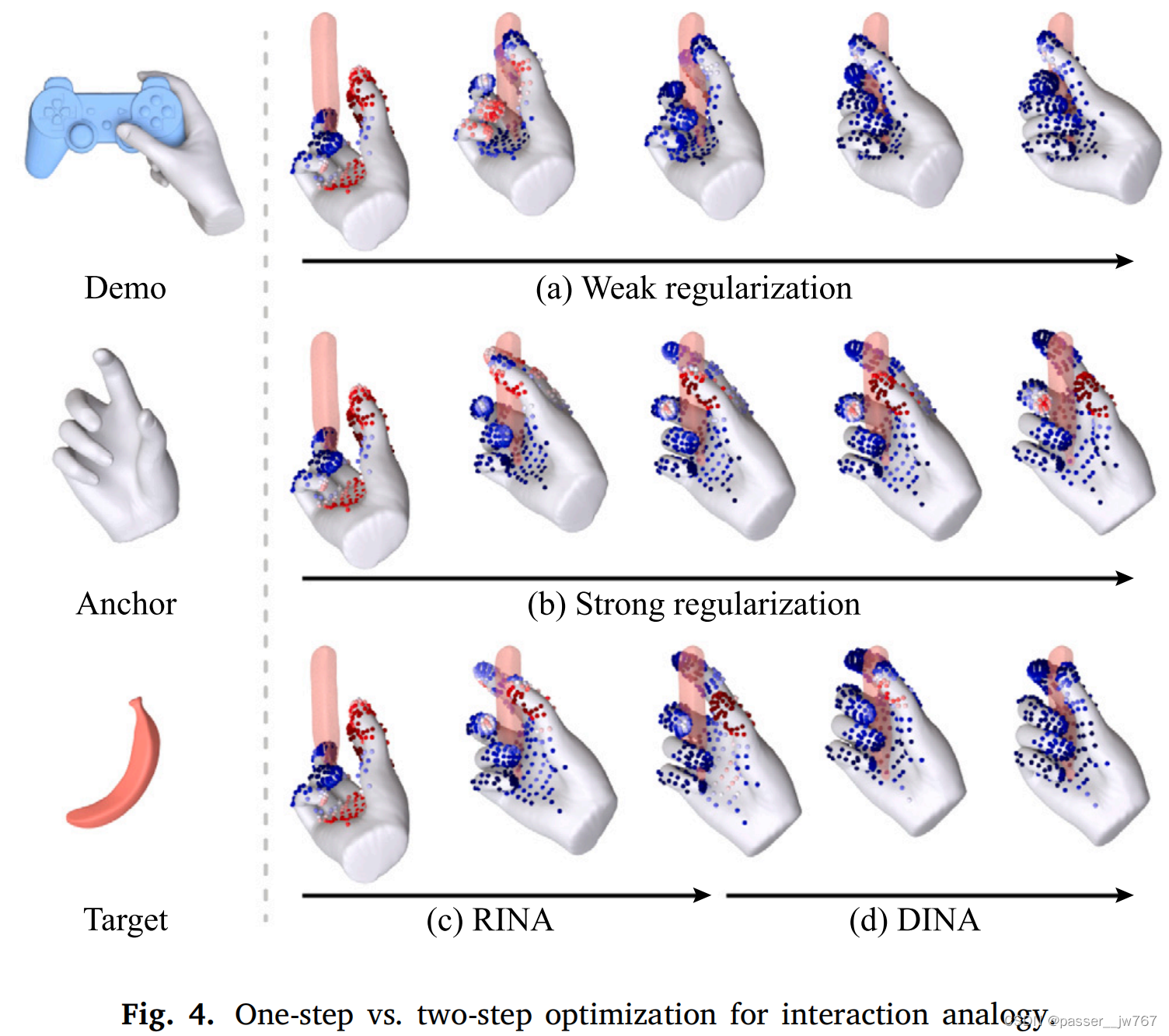
常见的方法是给$D$加上一个正则化项，来约束锚定物体的变形在一个合理的pose和shape下，但是作者发现很难平衡正则化项和目标函数的权重。太弱的正则化通常导致不自然的手部姿态（如上图(a)），太强的正则化又会过度约束手部姿态导致不能合理地抓握目标物体（如上图(b)）。

为了使优化更稳定，提出了两步优化方法。第一步是进行刚性变换，在获得了一个较好的初始交互位置后（如上图©），通过第二步局部变形来做局部变换（如上图(d)）。

5. 讨论，限制与未来工作

ITF和距离特征可以用于指导锚定对象全局姿态优化和局部变形，从而形成更类似于示例交互的交互。实验证明简单但富含信息量的表示相对其他现有方法带来了更加出人意料的结果。

限制与未来工作直接机翻了：

我们目前的方法有以下限制，我们计划在未来的工作中进行研究。首先，我们目前主要进行DINA手抓实验，这显然是一个突出的应用。虽然手只执行铰接运动，我们的itf驱动的优化没有假设或保证锚物体的分段刚度。在未来，在实验中表现出一般软体变形的锚定物体将是很有趣的。第二，即使在渗透损失的情况下，仍然可能出现物体交叉，特别是当演示有一个较大的接触区域，而目标在接触区域周围的几何形状相当不同时，如图10所示的失败例子所示。未来的改进是探索在这种情况下找到更好的平衡的方法。此外，我们的工作集中于与单一演示的交互类比，我们发现不同的目标对象可能有利于各种演示，以形成更好的交互。在这方面，如果有多个演示可用，如何选择最好的一个，甚至将它们结合起来，为交互类比提供最佳的指导是值得的。

这篇关于【计算机图形学】DINA: Deformable INteraction Analogy的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---