本文主要是介绍机器人动力学模型与阻抗控制MATLAB仿真，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
机器人刚体动力学由以下方程控制！！！
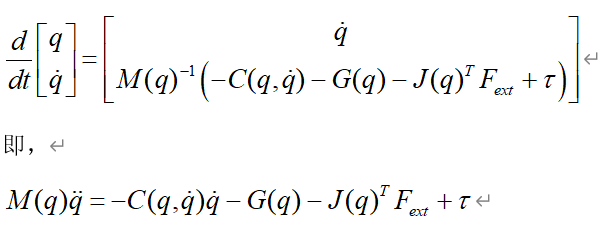
startup_rvc
mdl_puma560
p560.dyn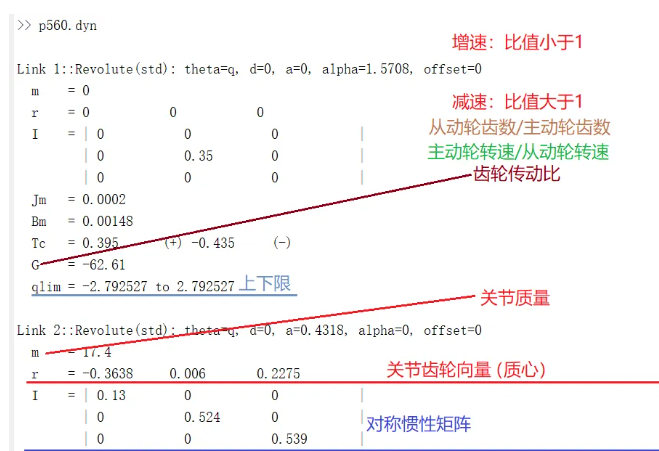
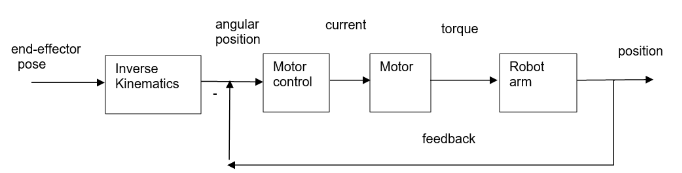
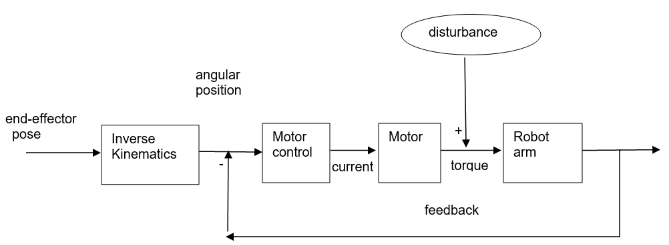
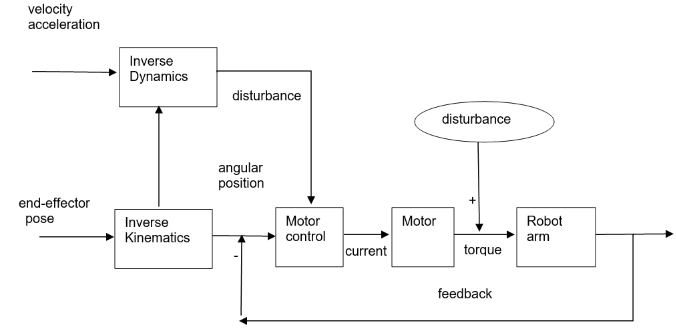
提前计算出来这些“disturbance”，然后在控制环路中将它“抵消”（有时候也叫前馈控制）
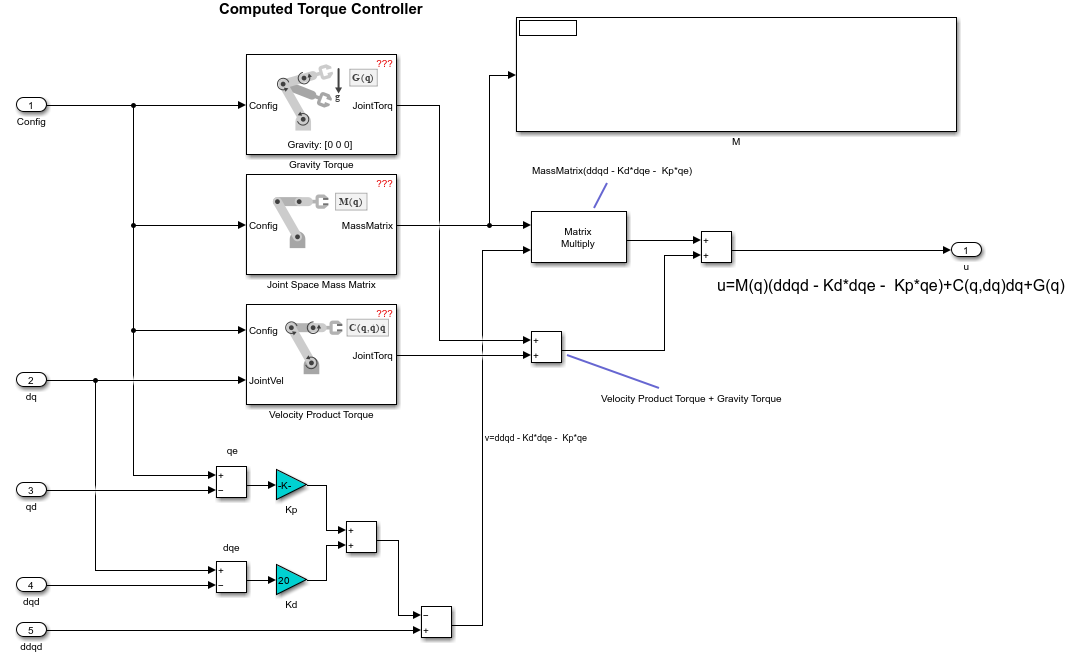
求出所需要的力矩，其中M项代表克服了机械臂的加速度惯量以及不同连杆之间的惯量影响所需力矩、C项代表了克服科里奥利力和离心力所需力矩、G项代表了克服地球引力力矩。
Inverse Dynamics叫做反向动力学，它的作用是输入想要的关节速度(qd)、关节加速度(qdd)、关节角度(q)，输出为每个关节所需要的力矩（u）。当然也有正向动力学（forward dynamics）,它的作用和反向动力学相反，输入关节角度（q）、关节速度（qd）、每个关节的力矩（u），输出为每个关节的加速度（qdd）
“前馈控制”的例子，它的作用是预先计算出所需的力矩，输入给控制器，“反馈”的存在是为了消除一些误差，例如摩擦力
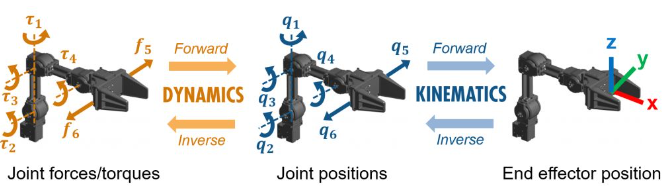
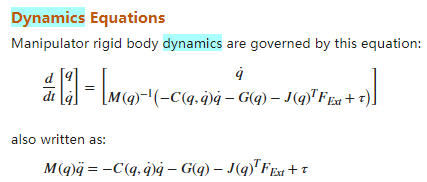
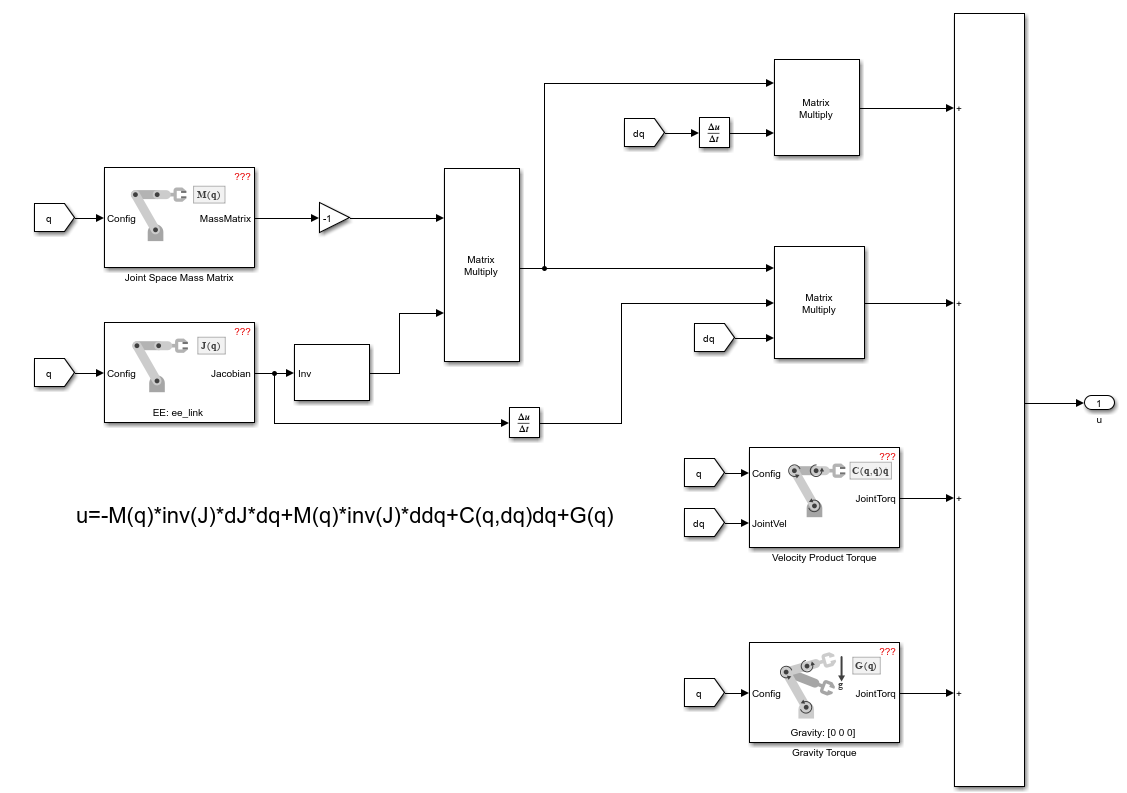
J=[-sin(q1)-sin(q1+q2) -sin(q1+q2);cos(q1)+cos(q1+q2) cos(q1+q2)];
d_J=[-dq1*cos(q1)-(dq1+dq2)*cos(q1+q2) -(dq1+dq2)*cos(q1+q2);-dq1*sin(q1)-(dq1+dq2)*sin(q1+q2) -(dq1+dq2)*sin(q1+q2)];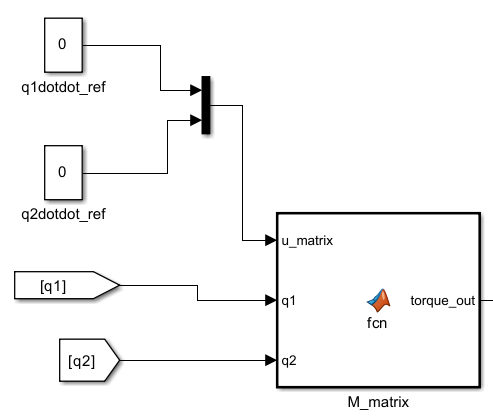
function torque_out = fcn(u_matrix,q1,q2)%% Robot Joint and mass parameters
g=9.81;
m1=0.3;
m2=1;
l1=0.2;
l2=0.2;%% B = M Matrix
B=[ (m1+m2)*l1^2+m2*l2^2+2*m2*l2*l1*cos(q2) (m2*l2^2+m2*l1*l2*cos(q2)) ; (m2*l2^2+m2*l1*l2*cos(q2)) m2*l2^2];torque_out= B* u_matrix ;end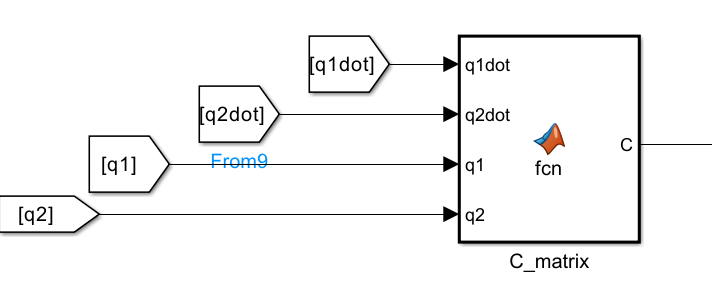
C=[-(m2*l1*l2*sin(q2)*(2*q1dot*q2dot+q2dot^2)) ; -m2*l1*l2*sin(q2)*q1dot^2];
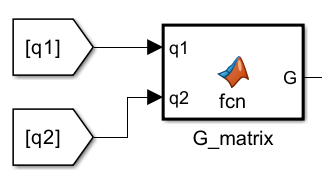
G=[(m1+m2)*g*l1*cos(q1)+m2*l2*g*cos(q1+q2) ; +m2*g*l2*cos(q1+q2)];
Minv=[ (m2*l2^2)/(((m1+m2)*l1^2*l2^2*m2)-(m2^2*l1^2*l2^2*cos(q2))) -(m2*l2^2+m2*l1*l2*cos(q2))/(((m1+m2)*l1^2*l2^2*m2)-(m2^2*l1^2*l2^2*cos(q2))) ; -(m2*l2^2+m2*l1*l2*cos(q2))/(((m1+m2)*l1^2*l2^2*m2)-(m2^2*l1^2*l2^2*cos(q2))) ((m1+m2)*l1^2+m2*l2^2+2*m2*l2*l1*cos(q2))/(((m1+m2)*l1^2*l2^2*m2)-(m2^2*l1^2*l2^2*cos(q2)))];
alfa = 6.7;beta = 3.4;
epc = 3.0;eta = 0;
m1 = 1;l1 = 1;
lc1 = 1/2;I1 = 1/12;
g = 9.8;
e1 = m1*l1*lc1-I1-m1*l1^2;
e2 = g/l1;M = [alfa+2*epc*cos(q2)*eta*sin(q2),beta+epc*cos(q2)+eta*sin(q2);beta+epc*cos(q2)+eta*sin(q2),beta];
C = [(-2*epc*sin(q2)+2*eta*cos(q2))*dq2,(-epc*sin(q2)+eta*cos(q2)*dq2;(epc*sin(q2)-eta*cos(q2)*dq1,0];
G = [epc*e2*cos(q1+q2)+eta*e2*sin(q1+q2)+(alfa-beta+e1)*e2*cos(q1);epc*e2*cos(q1+q2)+eta*e2*sin(q1+q2)];
J=[-sin(q1)-sin(q1+q2) -sin(q1+q2);cos(q1)+cos(q1+q2) cos(q1+q2)];
画圆轨迹：
xc=[1.0-0.2*cos(pi*t) 1.0+0.2*sin(pi*t)]';
dxc=[0.2*pi*sin(pi*t) 0.2*pi*cos(pi*t)]';
ddxc=[0.2*pi^2*cos(pi*t) -0.2*pi^2*sin(pi*t)]';
function [xd, yd] = fcn(r, t, w, x, y)alpha = t*w;xd = x + r*cos(alpha);
yd = y + r*sin(alpha);end
基于力矩的阻抗控制
动力学模型如下
阻抗控制模型如下
把这个阻抗模型得到的加速度带入到机器人动力学模型中，消除加速度ddx非线性项，得到控制律
基于模型的阻抗控制
笛卡尔空间的机器人动力学模型可描述为：
阻抗控制器可设计为：
————————————————————————————————
BA的存在导致系统耦合，如果希望在与环境交互过程中保持线性并解耦，需要测量接触力：
因此，
正向动力学
参考文献：
平面2R机器人运动学与动力学建模基于平面2R机器人谈谈运动学和动力学建模的应用
https://mp.weixin.qq.com/s/1gQTDHpyUkTMst_OdVFlnw
MATLAB 中的机械臂算法——动力学系列技术文章https://mp.weixin.qq.com/s/opQcpv02sysIcz8seg3lkQ
这篇关于机器人动力学模型与阻抗控制MATLAB仿真的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
