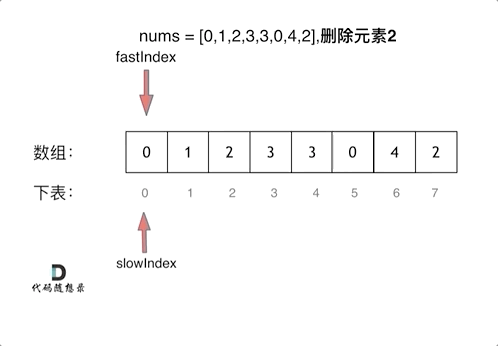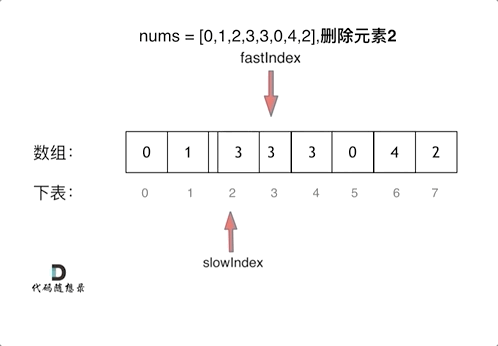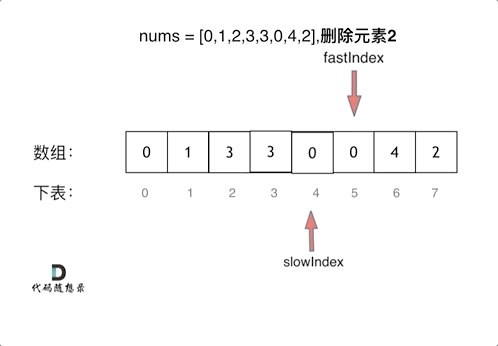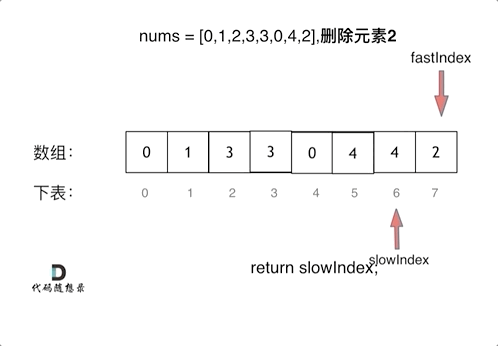
455专题

数组与贪心算法——605、121、122、561、455、575（5简1中）

605. 种花问题（简单）假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false 。解法一

Leetcode 455. 分发饼干----python

1. 题目描述假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i ，都有一个胃口值 gi ，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j ，都有一个尺寸 sj 。如果 sj >= gi ，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。注意：你可以假设胃口值

leetcode:455分发饼干

分发饼干假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。 public in

代码随想录算法训练营第29天（贪心）|455.分发饼干、376. 摆动序列、53. 最大子序和

455.分发饼干题目链接：455.分发饼干文档讲解：代码随想录状态：so easy 思路：对胃口和饼干大小排序，小胃口对应小饼干，不满足的话用下一块饼干试探。题解： public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int count = 0;int i

FANUC机器人SRVO-454和SRVO-455故障报警处理总结

FANUC机器人SRVO-454和SRVO-455故障报警处理总结公司内的一台FANUC机器人（型号：M-900iB；控制柜型号：R-30iB）正常运转过程中突然报警： SRVO-455 CPU看门狗（G:1 A:2），按Reset键无法消除该报警；查看SRVO-455故障报警的具体内容，如下图所示：由于现场没有备用的伺服放大器，所以只能尝试将控制柜断电处理；

day31贪心算法part01| 理论基础 455.分发饼干 376. 摆动序列 53. 最大子序和

**455.分发饼干 ** 视频讲解 | 力扣链接刚开始想到的，但是这样太暴力了，太笨了 class Solution {public:int findContentChildren(vector<int>& g, vector<int>& s) {// 胃口g 饼干尺寸sint result = 0;sort(s.begin(), s.end());sort(g.begin(), g.

【代码随想录】【算法训练营】【第31天】 [455]分发饼干 [376]摆动序列 [53]最大子序和

前言思路及算法思维，指路代码随想录。题目来自 LeetCode。 day 31，放假前的周五，总是令人激动的~ 题目详情 [455] 分发饼干题目描述 455 分发饼干解题思路前提：思路：贪心算法，小饼干优先满足较小胃口。重点：局部最优解，叠加整体最优解。代码实现 C语言排序后，小饼干优先小胃口 int cmp(void *p1, void *p2)

代码随想录算法训练营day31|455.分发饼干、376.摆动序列、53.最大子序和

分发饼干 455. 分发饼干 - 力扣（LeetCode）贪心算法，让每个饼干给到能够满足的孩子，所以需要对饼干尺寸和孩子的满足值先进行排序，然后针对每一个饼干的尺寸，挑选恰好能够满足的孩子（这里表述可能不准确，即从大到小，都选择能够满足的孩子，满足后结果返回值加1），这里选用while循环比较简单，具体代码如下。 class Solution {public:int findConte

【代码随想录算法训练Day31】LeetCode 455.分发饼干、LeetCode 376.摆动序列、LeetCode 53.最大子数组和

Day31 贪心所谓贪心，就是不断追求局部最优解的过程。如果一个问题能通过局部最优解通向整体最优解，那么这样的问题就可以用贪心算法解决。准确的来说贪心并不是一种算法，而是一种题目的特征，只要题目有这种特征，我们就能通过这种方法解题。 LeetCode 455.分发饼干用较大的饼干满足胃口最大的孩子，减少浪费。用较小的饼干满足胃口较小的孩子，使得满足的孩子数量最多。所以开始前要排序，然后

代码随想录第三十一天打卡|455.分发饼干，376. 摆动序列， 53. 最大子序和，

455.分发饼干代码随想录 class Solution {public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int left=0,res=0;for (int right=0;right<s.size();rig

LeetCode-Greedy-455. Assign Cookies

问题：https://leetcode.com/problems/assign-cookies/?tab=Description Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie. Each

代码随想录算法训练营day34 | 455.分发饼干、376. 摆动序列、53. 最大子序和

理论基础贪心的本质是选择每一阶段的局部最优，从而达到全局最优。刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。 455.分发饼干 result和j变化一致，可以去除一个 class Solution:def findContentChildren(self, g: List[int], s: List[int]) -> int:# 分配

代码随想录算法训练营第三十四天 | 理论基础、455.分发饼干、376、摆动序列、53.最大子序和

目录理论基础 455.分发饼干思路代码 376.摆动序列思路代码 53.最大子序和思路代码理论基础代码随想录 455.分发饼干代码随想录思路可以是大饼干优先满足大胃口，也可以是小饼干优先满足小胃口。代码 class Solution:def findContentChildren(se

LeetCode 455. Assign Cookies

455. Assign Cookies 一、问题描述 Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie. Each child i has a greed factor gi, whic

C++ 455. 分发饼干

文章目录一、题目描述二、参考代码一、题目描述示例 1: 输入: g = [1,2,3], s = [1,1] 输出: 1 解释: 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。所以你应该输出1。示例 2: 输入: g = [1,2], s = [1,2,3] 输出: 2 解

LeetCode - 455. 分发饼干

描述假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。示例 1: 输入

[力扣题解]455. 分发饼干

题目：455. 分发饼干思路贪心法代码 class Solution {public:int findContentChildren(vector<int>& g, vector<int>& s) {int cookie_i, belly_i, result = 0;// 满足的小孩数 : result// 胃口: g// 饼干: ssort(g.begin(), g.end())

Day 31 贪心算法理论基础 455.分发饼干 376. 摆动序列 53. 最大子序和

贪心算法理论基础贪心算法的本质：选择每一个阶段的局部最优，从而达到系统的整体最优；贪心的套路就是没有套路，最好的策略就是举反例，因为大多数时候并不要求严格证明，只需要得到普遍性结论即可；贪心算法一般分为如下四步：将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解做题的时候，只要想清楚局部最优是什么推导出全局最优就够了。

算法刷题Day31 | 455.分发饼干、376. 摆动序列、53. 最大子数组和

目录 0 引言1 分发饼干1.1 我的解题1.2 更好的解题 2 摆动序列2.1 我的解题2.2 我的错误原因（GPT分析）2.3 改进 3 最大子数组和3.1 我的解题 🙋‍♂️ 作者：海码007📜 专栏：算法专栏💥 标题：算法刷题Day31 | 455.分发饼干、376. 摆动序列、53. 最大子序和❣️ 寄语：书到用时方恨少，事非经过不知难！ 0 引言

代码随想录算法训练营第三十一天|455.分发饼干，376. 摆动序列，53. 最大子序和

贪心算法贪心的本质是选择每一阶段的局部最优，从而达到全局最优。贪心算法没有模板。题目：455.分发饼干假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j]。如果 s[j]= g[i]，我们可以将这个饼干 j 分配给孩子 i ，

代码随想录｜Day31｜贪心算法 part01｜● 455.分发饼干 ● 376. 摆动序列 ● 53. 最大子序和

455.分发饼干 class Solution: def findContentChildren(self, g: List[int], s: List[int]) -> int: # if not g or not s: 可以没有这句，因为后面index>=0已经涵盖了 # return 0 g.sort()

代码随想录第32天|455.分发饼干 376. 摆动序列

理论基础贪心算法核心：选择每一阶段的局部最优，从而达到全局最优。 455.分发饼干 455. 分发饼干 - 力扣（LeetCode）代码随想录 (programmercarl.com)455. 分发饼干 - 力扣（LeetCode）贪心算法理论基础！_哔哩哔哩_bilibili 假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个

代码随想录算法训练营第三十一天| 理论基础，455.分发饼干， 376. 摆动序列，53. 最大子序和

题目与题解参考资料：贪心算法理论基础 455.分发饼干题目链接：455.分发饼干代码随想录题解：455.分发饼干视频讲解：贪心算法，你想先喂哪个小孩？| LeetCode：455.分发饼干_哔哩哔哩_bilibili 解题思路：先对小孩胃口g和饼干分量s进行排序，然后对于小孩的胃口，从小到大分配饼干。如果当前饼干不能满足当前小孩胃口，就继续看下一个

算法训练营第31天|LeetCode 455.分发饼干 376.摆动序列 53.最大子序列和

LeetCode 455.分发饼干题目链接： LeetCode 455.分发饼干解题思路：从孩子小到大，找到最小能满足孩子的饼干，之后看最多能满足几个孩子。代码： class Solution {public:int findContentChildren(vector<int>& g, vector<int>& s) {int count = 0;map<int,int>m

代码随想录第31天 | 455.分发饼干、376. 摆动序列、53. 最大子序和

一、前言参考文献：代码随想录今天的内容是贪心算法，这个算法分为两个极端，一个极端是很简单，靠常识就可以解出来，另外一个是，你怎么想也想不出来，只能看题解的那种。 and 对第一天和第二天的内容进行复习；二、分发饼干 1、思路：本题的核心思路是找到局部最优解，就推出全局最优解。（1）显然我们需要找到最大的饼干，然后判断这个饼干是否能满足胃口最大的孩子，若能满足就可以找次胃口

UVa 455 周期串（Periodic Strings）

题目意思: 如果一个字符串可以由某个长度为k的字符串重复多次得到,则称该串以k为周期。例如，abcabcabcabc以3为周期(注意6，12也为周期 )，求的是最小周期。实现： #include<stdio.h>#include<string.h>#define maxn 100000int main(){char s[maxn];int n, i;