数组与贪心算法——605、121、122、561、455、575（5简1中）

本文主要是介绍数组与贪心算法——605、121、122、561、455、575（5简1中），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

605. 种花问题（简单）

假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false 。

解法一、贪心

先种满，数数满了多出来几朵，再讨论n在不在范围内。对边界要求有点高。。

题解里较完美的一个if条件：

if ((i == 0 || f[i - 1] == 0) && f[i] == 0 && (i == m - 1 || f[i + 1] == 0))

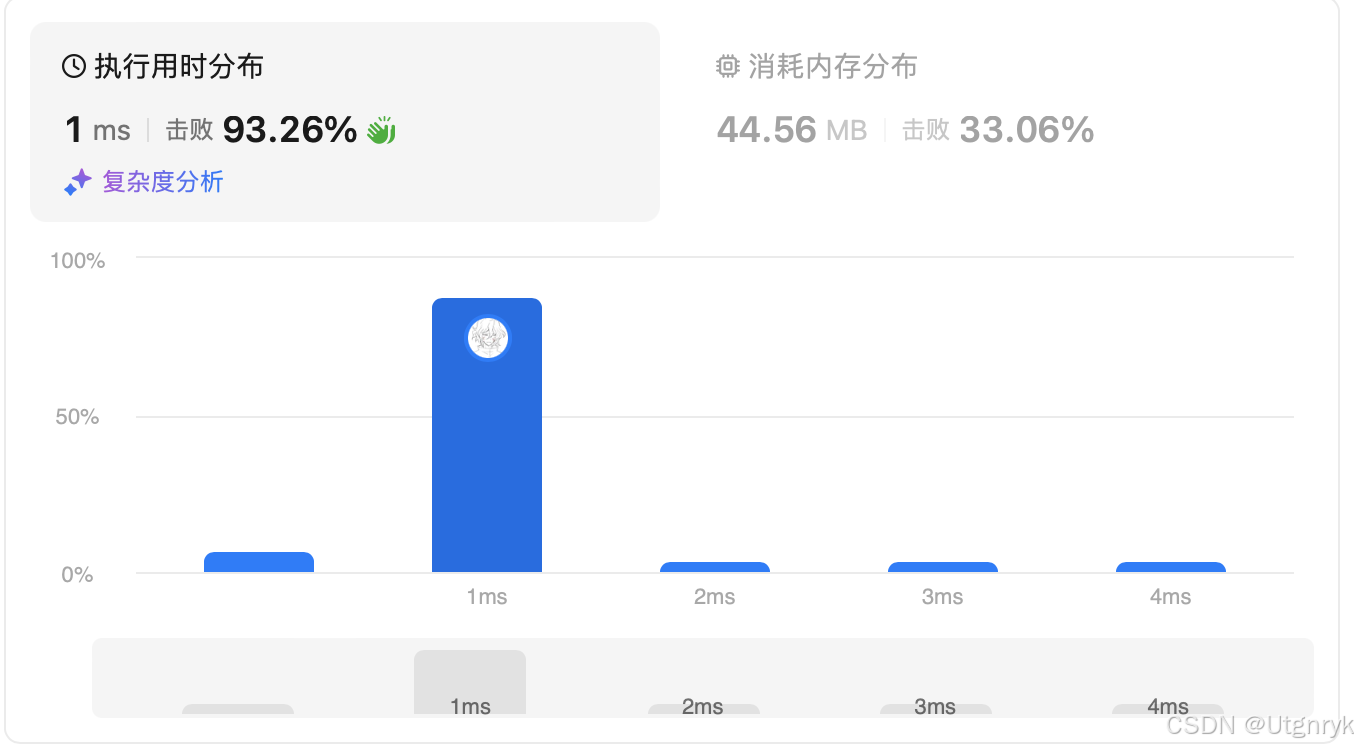
class Solution {public boolean canPlaceFlowers(int[] flowerbed, int n) {int num = flowerbed.length;int res = 0;if(num == 1){return n==0 || flowerbed[0] == 0 && n == 1 ;}else if(num == 2){return n==0 || ((flowerbed[0] == 0 && flowerbed[1] == 0) && n == 1);}for(int i = 0; i < num;i++){if(i == 0 && flowerbed[0] == 0 && flowerbed[1] == 0){flowerbed[0] = 1;res++;}else if(i == num-1 && flowerbed[i-1] == 0 && flowerbed[i] == 0){res++;}else if(i > 0 && i < num - 1 && flowerbed[i] != 1 && flowerbed[i+1] != 1 && flowerbed[i-1] != 1){flowerbed[i] = 1;res++;}}return n <= res;}
}

121. 买卖股票的最佳时机(简单)

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

解法一、暴力（超时）

一开始确实想不动脑子来着（

public class Solution {public int maxProfit(int[] prices) {int maxprofit = 0;for (int i = 0; i < prices.length - 1; i++) {for (int j = i + 1; j < prices.length; j++) {int profit = prices[j] - prices[i];if (profit > maxprofit) {maxprofit = profit;}}}return maxprofit;}
}

解法二、类dp

但不需要维护一个dp数组，只需要维护一个从0-k（0<=k<n）的最小买入值就好

class Solution {public int maxProfit(int[] prices) {int min = prices[0];int profit = 0;for(int i = 1;i < prices.length;i++){profit = Math.max(prices[i] - min,profit);min = Math.min(min,prices[i]);}return profit;}
}

122. 买卖股票的最佳时机 II（中等）

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的最大利润 。

解法一、贪心

本质思想就是一旦有钱赚马上买入卖出。注意：贪心只能模拟思想过程，不是实际交易过程。如对于[1,3,4]，贪心是1买3卖、3买4卖，交易过程是1买4卖。两者利益等价，行为不等价。

本题还有很多其他类型，尤其是dp/递增栈，但果然还是放在dp专题里做比较好吧~这方面就不贪心了！

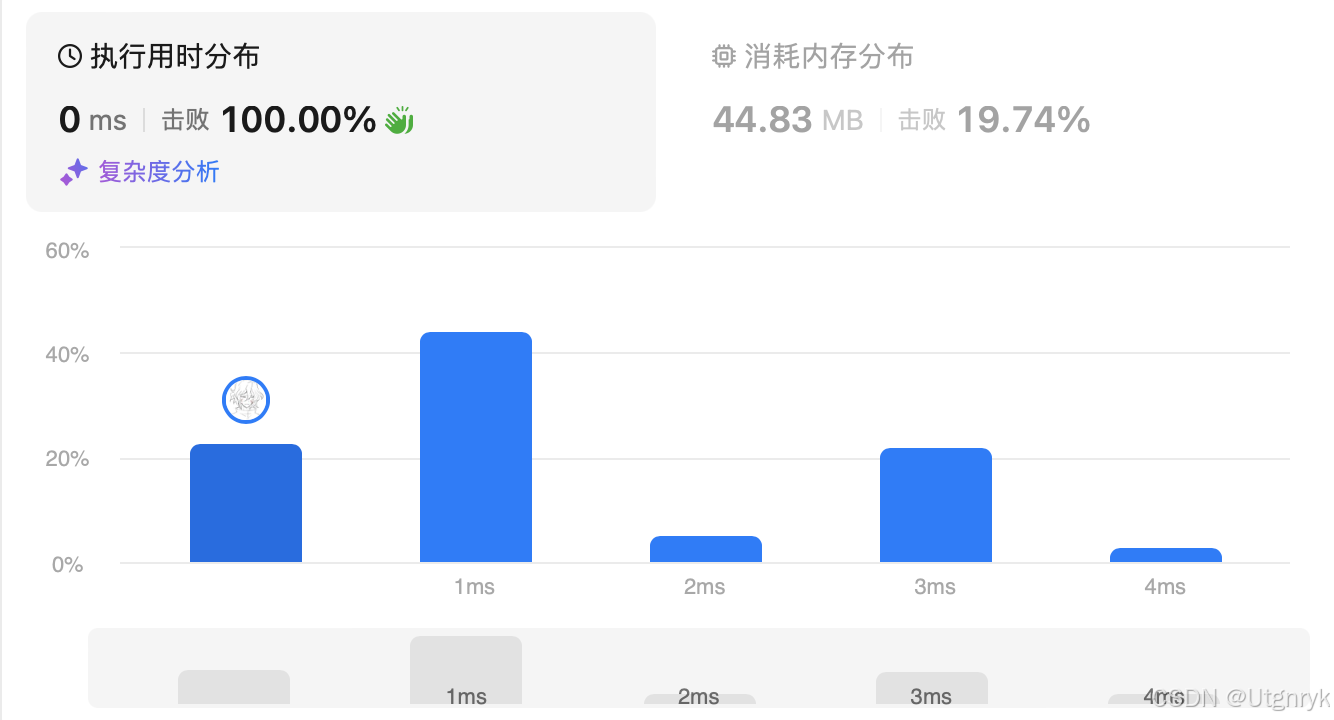
class Solution {public int maxProfit(int[] prices) {int profit = 0;if(prices.length < 2)return 0;for(int i = 1;i < prices.length;i++){if(prices[i] > prices[i-1])profit += prices[i] - prices[i-1];}return profit;}
}

561. 数组拆分(简单)

给定长度为 2n 的整数数组 nums ，你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ，使得从 1 到 n的 min(ai, bi) 总和最大。

返回该 最大总和 。

解法一、排序

要取最大，也就是尽量把小的和小的堆一起，大的和大的堆一起。所以先排序，排序后数组偶数位置的和就是所求。

class Solution {public int arrayPairSum(int[] nums) {Arrays.sort(nums);int n = nums.length,sum = 0;for(int i = 0;i < n;i +=2){sum+=nums[i];}return sum;}
}

解法二、数组排序

从代码示例那边看到的。这个和之前看到的那个取maxSum、minSum然后/2的技法其实有点像，桶排序虽然麻烦但是耗时真的很低。这里直接取gpt的解释吧。

index 用来追踪当前已经遍历的数值的累计个数。

res 是用于存储最终的结果。

每当 arr[i] > 0，意味着索引 i 对应的数值在 nums 中出现过，代码会根据当前的 index 和 arr[i] 的值来计算部分结果：

((index + 1) % 2 + arr[i]) / 2 这个表达式与确定中位数位置相关，它用于决定是否将该数值纳入 res的计算。

(i - 10000) 将索引 i 转换回原来的数值范围（因为我们之前对 nums 的数值进行了偏移处理）。

最后，index = index + arr[i] 用于更新累计的数值个数。

((index + 1) % 2 + arr[i]) / 2 这个表达式的作用是用于控制在遍历过程中，是否选择将当前 i 对应的数值 (即 i - 10000) 贡献给最终的 res 结果。让我们一步一步拆解它的含义：

1. index + 1

index 是用来记录遍历到当前位置之前，总共处理过的元素的个数。index + 1 表示当前的元素是所有已经遍历过的元素中的第几个。

2. % 2

对 index + 1 取模 2 的作用是确定当前这个元素是偶数还是奇数。它会返回两种情况：

当 index + 1 是奇数时，(index + 1) % 2 = 1。

当 index + 1 是偶数时，(index + 1) % 2 = 0。

这个结果决定了后续表达式的一个偏移调整。

3. arr[i]

arr[i] 表示当前索引 i 对应的数值在 nums 数组中出现的次数。

4. ((index + 1) % 2 + arr[i])

这一步是把 (index + 1) % 2 和 arr[i] 的值加起来：

如果当前是奇数个元素 ((index + 1) % 2 = 1)，那么结果就是 1 + arr[i]。

如果当前是偶数个元素 ((index + 1) % 2 = 0)，那么结果就是 0 + arr[i]。

这相当于调整了 arr[i] 的数值，使得某些条件下它多加 1 或不变，这和计算中位数的位置有关系。

5. / 2

这一步是对整个表达式进行除以 2：

如果 arr[i] 是偶数或者 (index + 1) % 2 是 0，那么 (index + 1) % 2 + arr[i] 是偶数，除以 2 后返回一个整数。

如果 arr[i] 是奇数，并且 (index + 1) % 2 = 1，这会使得奇数变为偶数的一半。

总体意义

这个表达式的作用在于，在遍历过程中，根据当前遍历的元素顺序（index）以及该元素的出现次数（arr[i]），判断要不要取一半的数值（除以 2），这样就可以控制贡献给 res 的数值。在处理中位数相关的算法时，这个操作可以帮助判断中位数所在位置以及应取多少值。

举例

假设：

arr[i] = 3 表示当前这个数出现了 3 次，

index + 1 = 5 表示当前是第 5 个元素，

那么：

(index + 1) % 2 = 1，所以 ((index + 1) % 2 + arr[i]) = 1 + 3 = 4，

/ 2 后结果是 2，表示将当前的数值贡献 2 次。

这个操作对中位数或者其他与位置相关的统计操作有帮助。

class Solution {public int arrayPairSum(int[] nums) {if (nums.length <= 1800) {Arrays.sort(nums);int sum = 0;for (int i = 0; i < nums.length; i = i + 2) {sum = sum + nums[i];}return sum;} else {// 在该用数组排序的时候又把这件事忘了个干净int[] arr = new int[20001];for (int i = 0; i < nums.length; i++) {arr[nums[i] + 10000]++;}int index = 0;int res = 0;for (int i = 0; i < arr.length; i++) {if (arr[i] > 0) {res = res + ((index + 1) % 2 + arr[i]) / 2 * (i - 10000);index = index + arr[i];}}return res;}}
}

455. 分发饼干（简单）

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是满足尽可能多的孩子，并输出这个最大数值。

解法一、排序+双指针

先排序。如果饼干比当前孩子胃口值小，那么饼干值往后挑。否则，i++，j++，计入结果。

class Solution {public int findContentChildren(int[] g, int[] s) {int i = 0,j = 0,res = 0;Arrays.sort(g);Arrays.sort(s);while(i < g.length && j < s.length){while(i < g.length && j < s.length && s[j] < g[i])j++;if(i < g.length && j < s.length && s[j] >= g[i]){i++;j++;res++;}}return res;}
}

稍微改善一些（2ms）的情况。在这次的循环里，以孩子都吃到为前提条件，如果饼干用完，则结束，减少了反复判断。

 public int findContentChildren0(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int result = 0;int j = 0;for (int i = 0; i < g.length; i++) {while (j < s.length && g[i] > s[j]) {j++;}if (j >= s.length) {break;}j++;result++;}return result;}

575. 分糖果（简单）

Alice 有 n 枚糖，其中第 i 枚糖的类型为 candyType[i] 。Alice 注意到她的体重正在增长，所以前去拜访了一位医生。

医生建议 Alice 要少摄入糖分，只吃掉她所有糖的 n / 2 即可（n 是一个偶数）。Alice 非常喜欢这些糖，她想要在遵循医生建议的情况下，尽可能吃到最多不同种类的糖。

给你一个长度为 n 的整数数组 candyType ，返回： Alice 在仅吃掉 n / 2 枚糖的情况下，可以吃到糖的最多种类数。

解法一、枚举

只要品种不同就过，如果达到满值就break

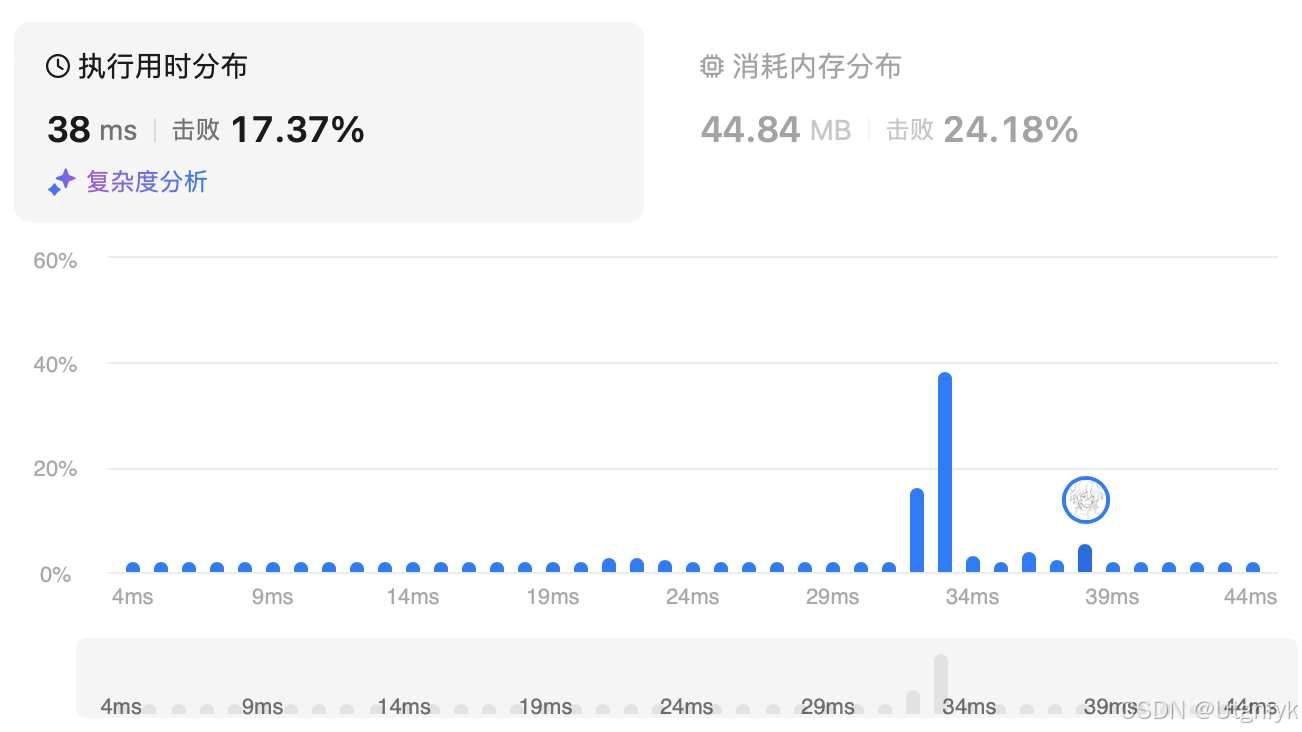
class Solution {public int distributeCandies(int[] candyType) {int res = 0,n2 = candyType.length;Arrays.sort(candyType);for(int i = 0;i < n2;i++){if(res == n2/2)return n2/2;res++;while(i < n2-1 && candyType[i]==candyType[i+1])i++;}return res;}
}

解法二、数据结构去重

本质上就是统计种类，然后返回Math.min(n/2，m)的东西，只要能够统计种类，什么方法都可以。

class Solution {public int distributeCandies(int[] candyType) {Set<Integer> set = new HashSet<Integer>();for (int candy : candyType) {set.add(candy);}return Math.min(set.size(), candyType.length / 2);}
}作者：力扣官方题解
链接：https://leetcode.cn/problems/distribute-candies/solutions/1072396/fen-tang-guo-by-leetcode-solution-l4f6/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。