3264专题

POJ 3264 RMQ--ST 算法

Balanced Lineup Time Limit: 5000MS Memory Limit: 65536KB 64bit IO Format: %I64d & %I64u Submit Status Description For the daily milking, Farmer John’s N cows (1 ≤ N ≤ 50,000) always line up in the

HDU 3264 Open-air shopping malls（二分+圆交）

HDU 3264 Open-air shopping malls 题目链接题意：给定一些圆，求以一个圆的圆心为圆心，自己定一个半径，使得和其他所有圆交面积都大于该圆的一半，求这个半径的最小值思路：很显然的二分半径，判断方法就枚举一个圆心，然后和每个圆求圆交面积即可代码： #include <cstdio>#include <cstring>#include <c

Balanced Lineup （poj-3264）

RMQ解决方案： #include <iostream>#include <math.h>#define max(a,b) ((a>b)?a:b)#define min(a,b) (a<b?a:b)using namespace std;const int maxn=50001;int h[maxn];int mx[maxn][16],mn[maxn][16];int

POJ 3264 Balanced Lineup RMQ / 线段树

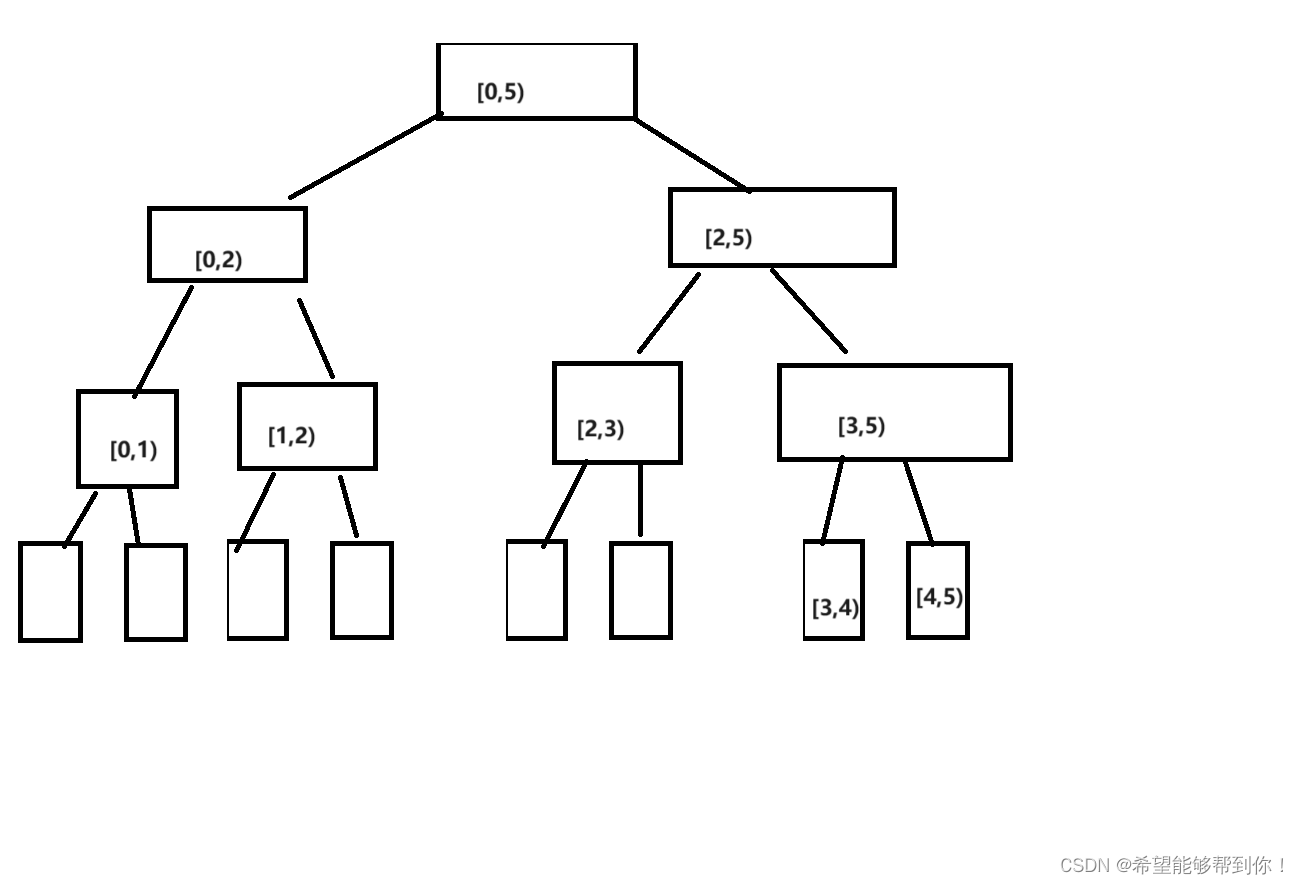
题意：给出一个队列，找出指定区间的最大值与最小值。题解：RMQ, 注意边界需要理清楚。参考http://www.cnblogs.com/cnjy/archive/2009/08/30/1556566.html RMQ(Range Minimum/Maximum Query)问题： RMQ问题是求给定区间中的最值问题。当然，最简单的算法是O(n)的，但是对于查询次数很多（设

poj 两道简单线段树 3264 3468

3264 http://poj.org/problem?id=3264 Balanced Lineup Time Limit: 5000MS Memory Limit: 65536KTotal Submissions: 46287 Accepted: 21709Case Time Limit: 2000MS Description For the daily milking, Fa

Balanced Lineup POJ-3264（线段树）

For the daily milking, Farmer John’s N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things

POJ 3264(ST实现RMQ)

题目链接：点击打开链接题目大意：给一个n和q，n代表有n个数，q代表q次查询。每次查询输入两个数字a,b，问你从第a个数字到第b个数字间的最大值减去最小值的值是多少。题目思路：如果直接搜，查一次就O（n），铁定爆炸。这里线段树和ST算法都可以，线段树好像挺麻烦先学一波ST解法一会儿去学线段树，美滋滋。不过像这种单纯的求区间最值的问题，还是用ST比较好，因为ST算法预处理nlogn，

第二道用segment tree过的题。实现还是所有过的里面最慢的。segment tree的实现大同小异，但有人能1s+,2s+的很多,我猜是因为我query的时候都会先进去，如果所求的区间不在这个区间内又跳出，耗费了不少时间。最终险过还真是因为我把cin, cout改成了scanf,printf，这肯定是快了至少400ms的，但我之前已经讲局部变量(输入数据和segment tree)变成了全

POJ 3264 Balanced Lineup (线段树单点更新区间查询)

Balanced Lineup Time Limit: 5000MS Memory Limit: 65536KTotal Submissions: 36820 Accepted: 17244Case Time Limit: 2000MS Description For the daily milking, Farmer John's N cows (1 ≤ N ≤ 5

POJ 3264 Balanced Lineup (RMQ模板)

Balanced Lineup Time Limit: 5000MS Memory Limit: 65536KTotal Submissions: 65283 Accepted: 30409Case Time Limit: 2000MS Description For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) alway

poj 3264 线段树寻找最大最小值 SEGMENT TREE

Description For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. T

POJ 3264 Balanced Lineup 线段树

A - Balanced Lineup For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of t

poj 3264——Balanced Lineup

线段树 #include<iostream>#include<cstdio>using namespace std;#define maxn 50004#define ls (rt<<1)#define rs (rt<<1|1)#define mid ((t[rt].l+t[rt].r)>>1)struct tree{int l,r;int max,min;}t[maxn<<2

Balanced Lineup POJ - 3264（RMQ）

Balanced Lineup POJ - 3264 题目连接题意：给出一个数列，Q个询问，问区间[A, B]中最大值与最小值的差；思路：线段树可以做，维护最大最小值，直接查找就可以；但是现在要用RMQ做；何为RMQ？(Range Minimum/Maximum Query) 区间最值询问，通过O(nlogn)的预处理可以在O(1)的时间内找到区间的最值；下面以最大值为例：令Fm

POJ-3264 Balanced Lineup(RMQ)

Balanced Lineup Time Limit: 5000MSMemory Limit: 65536KTotal Submissions: 73096Accepted: 33626Case Time Limit: 2000MS Description For the daily milking, Farmer John’s N cows (1 ≤ N ≤ 50,000) alway

Pku oj 3264 Balanced Lineup（RMQ）

Balanced Lineup Time Limit: 5000MS Memory Limit: 65536KTotal Submissions: 46162 Accepted: 21674Case Time Limit: 2000MS Description For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000)

poj 3264 (summerIII O) j树状数组 ST表（区间最值查询）

#include<cstdio>#include<algorithm>#include<cmath>using namespace std;const int maxn= 100000+50;int n,m,a[maxn],mx[maxn][50],mn[maxn][50];//这里mx[maxn][范围内尽量取大一点]void init(){int m=floor(log((doubl

POJ 3264 Balanced Lineup 线段树 / 平方分割

一、题目大意给出一个长度为 n（n<=50000) 数组 arr，进行Q次查询（Q<=200000），每次查询的内容为数组arr在 [L , R] 的切片的极差（最大元素 - 最小元素）二、解题思路 1、线段树区间极差其实就是区间内最大值 - 区间内最小，那么就想到RMQ，用线段树去维护一个区间内的最大和最小元素，然后根据问题的区间 L 和 R，找到相关的线段树节点，从中找出最大