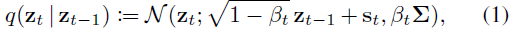高斯分布专题

为什么在很多应用中常采用正态分布/高斯分布、中心极限定理

为什么在很多应用中常采用正态分布/高斯分布？当我们由于缺乏关于某个实数上分布的先验知识而不知道该选择怎么样的形式时，正态分布是默认的比较好的选择，有两个原因：一，我们想要建模的很多分布的真实情况是比较接近正态分布的。中心极限定理说明很多独立随机变量的和近似服从正态分布。二，在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性。因此，我们可以认为正态分布是对模型加入的

概率论(二)-随机变量及其分布：分布函数F(x)、离散型随机变量【分布律：(0-1)分布、二项分布、泊松分布】、连续型随机变量【概率密度：均匀分布、指数分布、正态/高斯分布】、3σ法则、偏度、峰度

1 随机变量 2 离散型随机变量及其分布律 3 随机变量的分布函数 4 连续型随机变量及其概率密度 5 随机变量的函数的分布

机器学习数学公式推导之高斯分布

文章目录 1、介绍引入1.1 频率派的观点1.2 贝叶斯派的观点1.3 小结 2、数学基础2.1 二阶中心矩2.2 样本方差2.3 高斯分布2.3.1 一维情况 MLE2.3.2 多维情况本文参考 B站UP: shuhuai008 跳转 🌹🌹 1、介绍引入在统计学和概率论中， P ( x ∣ k ) P(x|k) P(x∣k) 通常表示在给定条件 k k

【高斯分布】

高斯分布作者：老师木关于高斯分布，@rickjin写了一个更好的文章，先推荐一下。 1733年，德-莫佛（De Moivre）在给友人分发的一篇文章中给出了正态曲线（这一历史刚开始被人们忽略）。1783年，拉普拉斯指出正态曲线方程适合于表示误差分布的概率。1809年，高斯发表了关于天体运行论的著作，在第二卷第三节中，他导出正态曲线适合于表示误差规律，同时承认拉普拉斯较早的推导。正态

利用均匀分布和中心极限定理产生正态分布（高斯分布）

中心极限定理：设随机变量序列 {Xi} \{X_i\}相互独立，具有相同的期望和方差，即 E(Xi)=μ,D(Xi)=σ

从高斯分布、机器人误差、EM算法到小球检测

Coursera上的课程（Robotics: Estimation and Learning），感觉讲得特别棒，写下自己的理解。高斯分布被广泛应用于对机器人误差的建模。在这篇笔记中，我们将会：介绍如何使用一元高斯分布、多元高斯分布和高斯混合模型对机器人误差进行建模。介绍求解这些高斯分布的算法。以小球检测这一实际应用来实践我们的模型和算法。 1. 一元高斯分布在这一节我们将介绍如何使用

[机器学习] 高斯过程 Gaussian-Process、CLT、高斯分布

代码参考：https://blog.csdn.net/weixin_39517202/article/details/111338017 视频参考：https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote15.html 参考：https://thegradient.pub/gaussian-process-not

【机器学习基础】概率分布之高斯分布

本系列为《模式识别与机器学习》的读书笔记。一，多元高斯分布考虑⾼斯分布的⼏何形式，⾼斯对于 x \boldsymbol{x} x 的依赖是通过下⾯形式的⼆次型： Δ 2 = ( x − μ ) T Σ − 1 ( x − μ ) (2.30) \Delta^{2} = (\boldsymbol{x} - \boldsymbol{\mu})^{T} \boldsymbol{\Sig

吴恩达机器学习笔记三十三发现异常事件高斯分布

例如飞机发动机的异常检测，假设只有两个特征，新的样本和之前的样本偏离的很多，就认为可能是异常的点。一种方法是密度估计（density estimation），计算训练样本的 x 落在某个区间的概率，当验证集的样本的概率小于一个很小的数时，认为这种情况是异常的。高斯分布(Guassian distribution，也叫正态分布，normal distribution,钟形分布，be

$中心极限定理之为何高斯分布在自然界中广泛存在$

中心极限定理之为何高斯分布在自然界中广泛存在

为什么自然界中许多随机现象可以用正态分布或近似正态分布来描述，在计算机视觉，图像处理，机器学习模型中应用尤为广泛。定理5.5 独立同分布情形下的中心极限定理设有独立同分布的随机变量序列且则对任意的实数有

高斯分布归一化、期望、二阶矩、方差推导证明

目录写在前面的唠叨：归一化推导证明：期望（一阶矩）推导证明：二阶矩推导证明：方差推导证明：写在前面的唠叨：最近这段时间一直在研究深度学习之类的东西，虽然如今对几种常见的神经网络都有了很好的了解，用起来也比较顺手，但是越学也越觉得瓶颈越来越明显了，最大的问题觉得还是数学基础不行，学习那些常见的模型已经把线性代数的知识捡的差不多了，而到了想自己设计模型的时候，才忽

SLAM基础知识-高斯分布

正态分布（高斯分布）学习笔记 - 知乎偏差(bias)、方差(variance)和噪音(noise)_noise variance-CSDN博客 --------------------------------------待更新--------------------------------------------------------------------------

概率论与数理统计——高斯分布的学习笔记

1 高斯分布的数学定义高斯分布的定义来自《概率论与数理统计·浙江大学》：

广义高斯分布(GGD)和非对称广义高斯分布(AGGD)的形状参数快速估计

0 引言广义高斯分布(generalized Gaussian distribution,GGD)和非对称广义高斯分布( asymmetric generalized Gaussian distribution,AGGD)被经常使用与图像/视频信号的统计分析，其形状参数常被用为图像的特征进行分类或回归。如在图像质量评价任务中，Anish Mittal等人提出的BRISQUE模型利用GGD拟

（2023|CVPR，Corgi，偏移扩散，参数高斯分布，弥合差距）用于文本到图像生成的偏移扩散

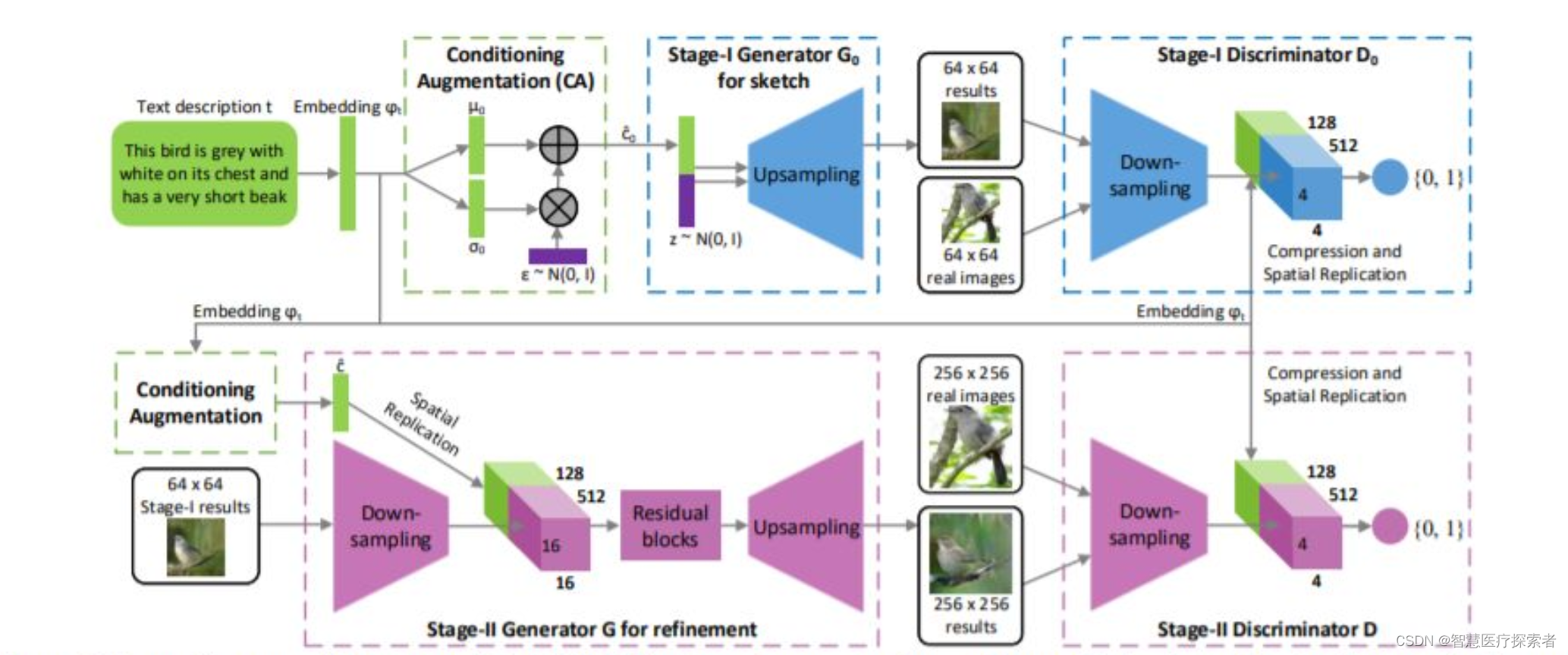
Shifted Diffusion for Text-to-image Generation 公众：EDPJ（添加 VX：CV_EDPJ 或直接进 Q 交流群：922230617 获取资料）目录 0. 摘要 1. 简介 2. 方法 2.1 偏移扩散 3. 实验 3.1 无监督文本到图像生成 3.2 无语言文本到图像生成 3.3 消融研究 4. 结论 S. 总结 S.1

$格密码：离散高斯与子高斯分布$

格密码：离散高斯与子高斯分布

高斯分布我们都很熟悉，但在格密码中会用到一种特殊的高斯分布，将其取名离散高斯分布（discrete Gaussian)。一. N维连续高斯分布给定一个正整数n，代表维度。一个正实数，代表标准差（高斯分布的标准差决定着图像的胖瘦，所以这个参数有的时候也叫“宽度”)。N维连续高斯分布的输入是N维向量，输出是一个正实数，也就是，概率密度函数如下：可以想到，如果把看成一个整体的话，新的

深度学习中的高斯分布

1 高斯分布数学表达 1.1 什么是高斯分布高斯分布(Gaussian Distribution)又称正态分布(Normal Distribution)。高斯分布是一种重要的模型，其广泛应用与连续型随机变量的分布中，在数据分析领域中高斯分布占有重要地位。高斯分布是一个非常常见的连续概率分布。由于中心极限定理(Central Limit Theorem)的广泛应用，高斯分布在统计学上非常重要。

正态分布（高斯分布）、Q函数、误差函数、互补误差函数

Matlab中本身有Q函数，即qfunc() [3] 其反函数是 qfuncinv() y = qfuncinv(x) 返回q函数的值为x的q函数的参数。输入x必须是一个实数数组，包含0到1之间的元素。下面的例子说明了qfunc和qfuncinv之间的反比关系。 x1 = [0 1 2; 3 4 5]; y1 = qfuncinv(qfunc(x1)) x2 = 0:.2:1;

正态分布（高斯分布）

正态分布（高斯分布）_Techblog of HaoWANG-CSDN博客_正态分布正态分布为什么常见？ - 阮一峰的网络日志【Matlab】正态分布常用函数normpdf_normcdf_norminv_normrnd_normfit_Find your love-CSDN博客_matlab正态分布函数

【Math】高斯分布的乘积 Product of Guassian Distribution【附带Python实现】

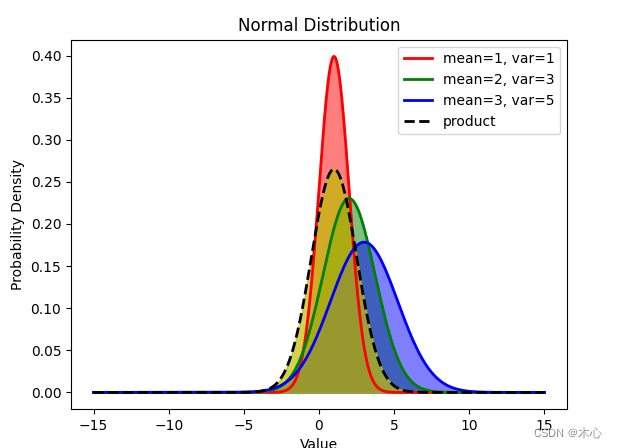
【Math】高斯分布的乘积 Product of Guassian Distribution【附带Python实现】文章目录【Math】高斯分布的乘积 Product of Guassian Distribution【附带Python实现】1.推导2. CodeReference 结果先放在前面 1.推导在学习PEARL算法的时候，encoder的设计涉及到

Python 图像处理: 生成二维高斯分布蒙版

在图像处理以及图像特效中，经常会用到一种成高斯分布的蒙版，蒙版可以用来做图像融合，将不同内容的两张图像结合蒙版，可以营造不同的艺术效果。 I=M∗F+(1−M)∗B I = M*F+(1-M)*B 这里 I I 表示合成后的图像，FF 表示前景图， B B 表示背景图，MM 表示蒙版，或者直接用蒙版与图像相乘, 形成一种渐变映射的效果。如下所示。 I=M∗

高斯分布画图

clc clear close all mu=[0,0];% 均值向量 Sigma=[1 0.5;0.5 1];% 协方差矩阵 [X,Y]=meshgrid(-3:0.1:3,-3:0.1:3);%在XOY面上，产生网格数据 p=mvnpdf([X(:) Y(:)],mu,Sigma);%求取联合概率密度，相当于Z轴 p=reshape(p,size(X));%

04、基于高斯分布的异常检测算法

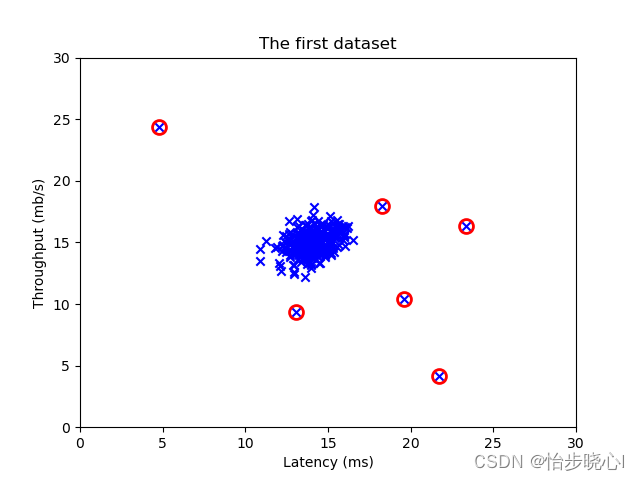
04、基于高斯分布的异常检测算法原理与实践开始学习机器学习啦，已经把吴恩达的课全部刷完了，现在开始熟悉一下复现代码。对这个手写数字实部比较感兴趣，作为入门的素材非常合适。数据的严重偏斜往往会导致监督学习算法面临巨大的挑战——尤其是在负样本数量稀缺的情况下，监督学习模型难以充分汲取必要的知识。这就引发了一个重要的问题：我们能否从这种极端不平衡的数据中成功地训练出一个有效的异常检测模型呢？答案

Python绘制高斯分布图像

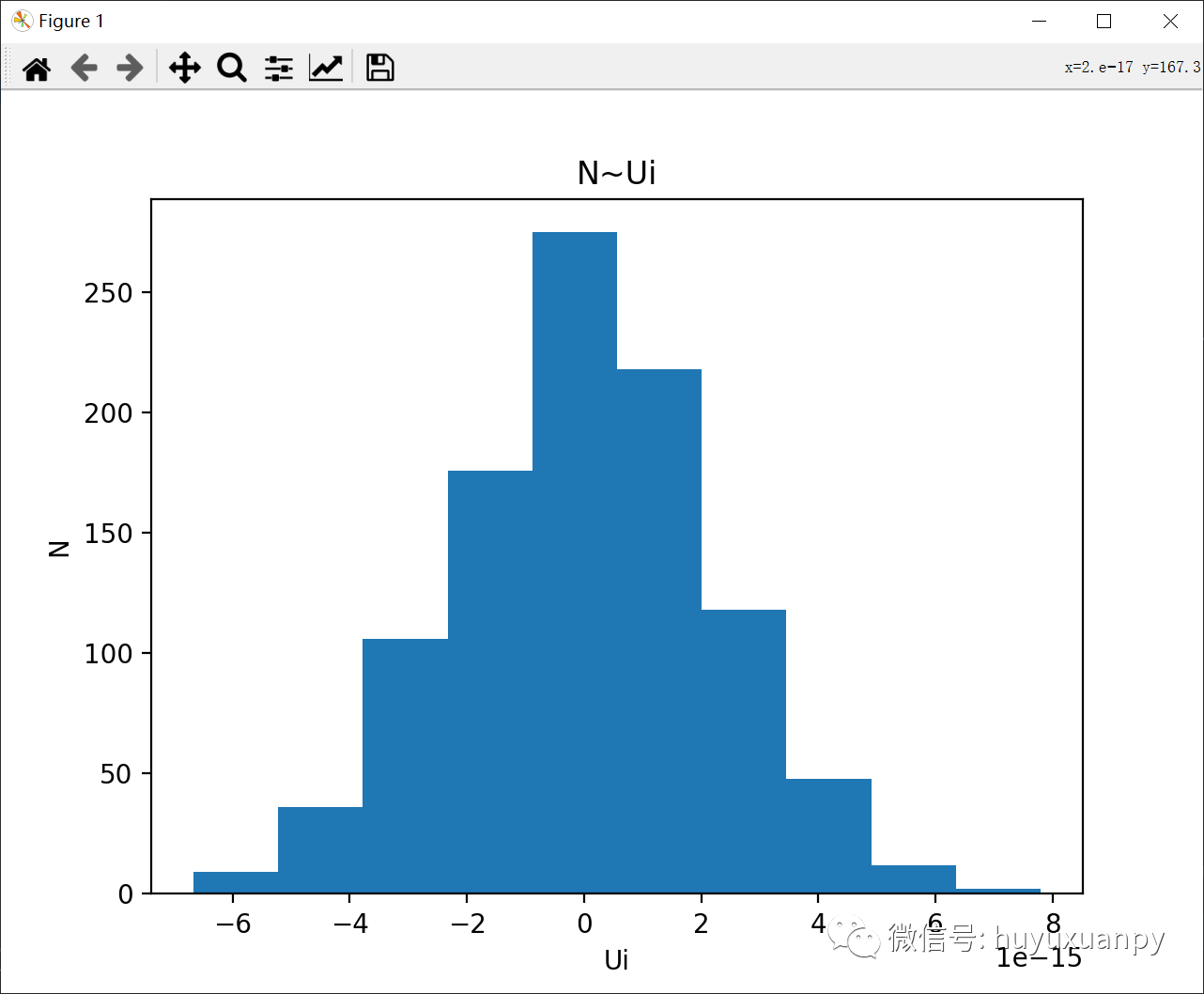
Python绘制高斯分布图像文章目录 Python绘制高斯分布图像一、需求介绍二、第一个任务三、第二个任务四、readme文件一、需求介绍我们这里旨在使用Python来绘制图像，其他的操作一概先不管，绘制高斯分布的图像。二、第一个任务代码 import matplotlib.pyplot as pltimport numpy as npfrom s

【概率图与随机过程】02 多元高斯分布：参数特征和几何意义

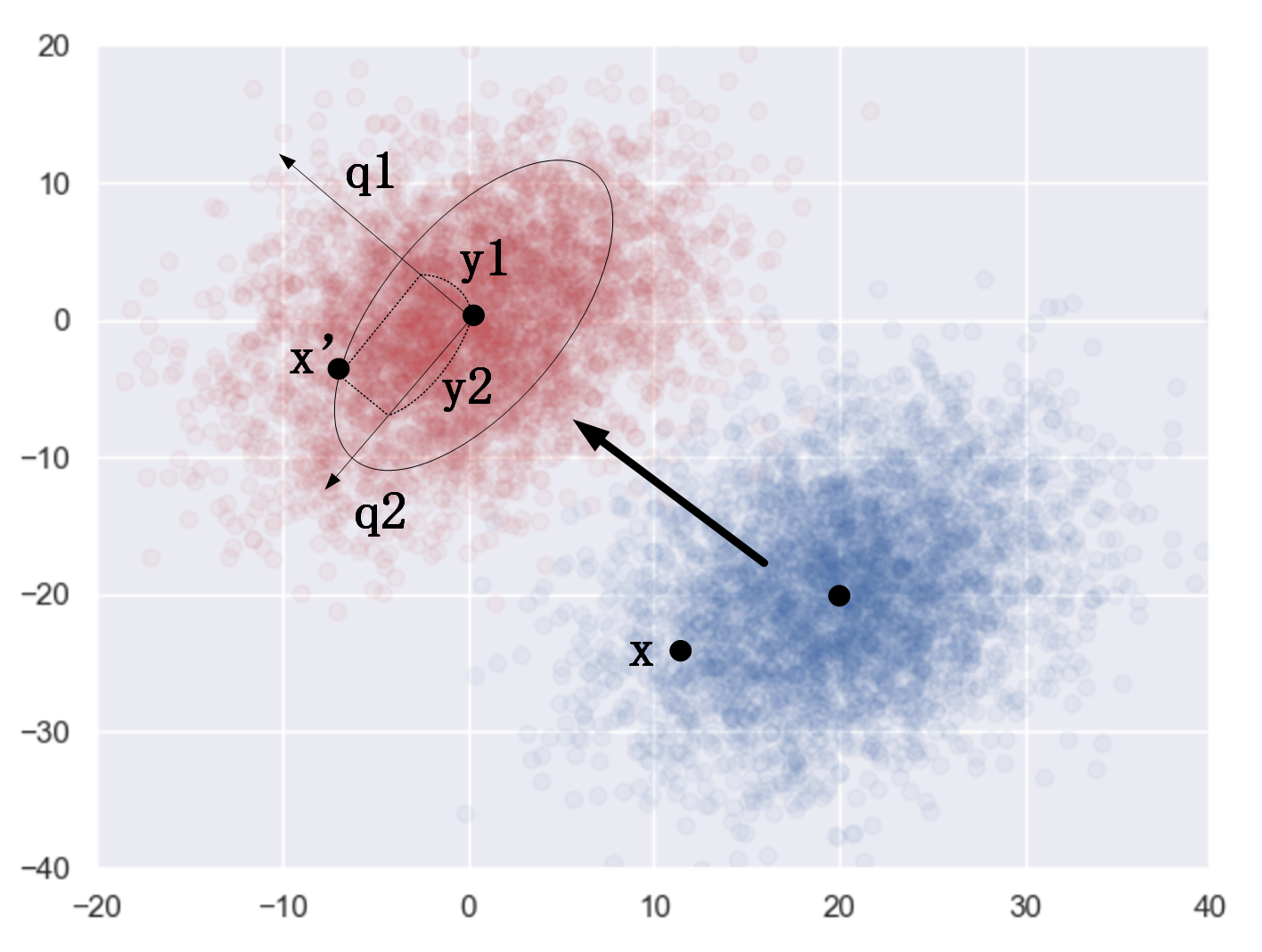
在上一讲里，我们重新回顾了一元高斯分布，并从这个分布入手，介绍了如何利用极大似然估计的方法对分布的两个参数：均值 μ \mu μ和方差 σ 2 \sigma^2 σ2进行估计，并从估计的有偏性和无偏性这个角度出发，对两个参数的极大似然估计值进行讨论和验证。 1.从一元分布到多元分布在这一讲，我们从一元高斯分布过渡到多元高斯分布，我们如何来理解多元高斯分布中的“多”呢？我们记得，在一元高斯

人工智能基础_机器学习007_高斯分布_概率计算_最小二乘法推导_得出损失函数---人工智能工作笔记0047

这个不分也是挺难的,但是之前有详细的,解释了,之前的文章中有, 那么这里会简单提一下,然后,继续向下学习首先我们要知道高斯分布,也就是,正太分布, 这个可以预测x在多少的时候,概率最大要知道在概率分布这个,高斯分布公式中,u代表平均值,然后西格玛代表标准差,知道了这两个数以后,带入正态分布的公式,可以看到就可以求出y的值来那么可以看到这里有派,还有e对吧,这两个自然界常