【Math】高斯分布的乘积 Product of Guassian Distribution【附带Python实现】

本文主要是介绍【Math】高斯分布的乘积 Product of Guassian Distribution【附带Python实现】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【Math】高斯分布的乘积 Product of Guassian Distribution【附带Python实现】

结果先放在前面

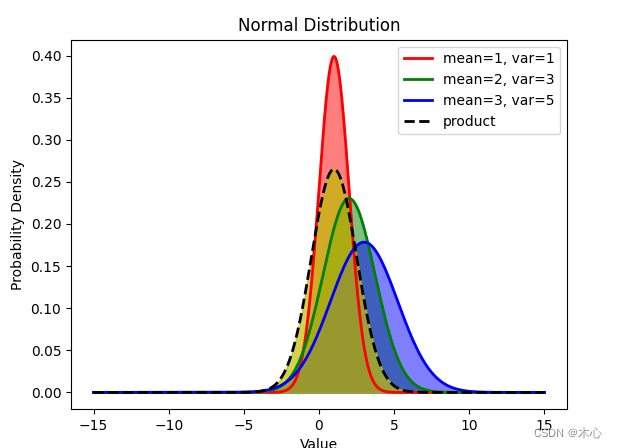
1.推导

在学习PEARL算法的时候，encoder的设计涉及到了高斯分布的乘积，对此有点疑问，进行推导补票。

首先高斯分布（Guassian Distribution）的概率密度函数为

$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})$$

通常将单位高斯分布记为$\mathcal{N}\sim (0,1)$，一般的高斯分布记为$\mathcal{N}\sim (\mu ,\sigma )$，其中$\mu$是高斯分布的均值（mean），$\sigma$是高斯分布的标准差（standard variance），${\sigma }^2$是高斯分布的方差（variance）。

​ 接下来推导高斯分布的乘积，假设有两个高斯分布，分别为
${\mathcal{N}}_1\sim ({\mu }_1,{\sigma }_1),{\mathcal{N}}_2\sim ({\mu }_2,{\sigma }_2)$，那么其概率密度函数的乘积为

$$\begin{array}{rl}{f}_1(x)f_2(x)& =\frac{1}{\sqrt{2\pi }{\sigma }_1}\exp (-\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2})\times \frac{1}{\sqrt{2\pi }{\sigma }_2}\exp (-\frac{(x-{\mu }_2{)}^2}{2{\sigma }_2^2})\\ & =\frac{1}{2\pi {\sigma }_1{\sigma }_2}\exp (-\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2}-\frac{(x-{\mu }_2{)}^2}{2{\sigma }_2^2})\end{array}$$

我们单独分析指数部分，

$$\begin{array}{rl}\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2}+\frac{(x-{\mu }_2{)}^2}{2{\sigma }_2^2}& =\frac{({\sigma }_1^2+{\sigma }_2^2)x^2-2x({\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2)+({\mu }_1^2{\sigma }_2^2+{\mu }_2^2{\sigma }_1^2)}{2{\sigma }_1^2{\sigma }_2^2}\\ & =\frac{x^2-2x\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}+\frac{{\mu }_1^2{\sigma }_2^2+{\mu }_2^2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}}{\frac{2{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}\\ & =\frac{(x-\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}{)}^2+\frac{{\mu }_1^2{\sigma }_2^2+{\mu }_2^2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}-(\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}{)}^2}{\frac{2{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}\\ & =\frac{(x-\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}{)}^2}{\frac{2{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}+\frac{\frac{{\mu }_1^2{\sigma }_2^2+{\mu }_2^2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}-(\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}{)}^2}{\frac{2{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}\end{array}$$

继续化简上面的常数部分

$$\begin{array}{rl}\frac{\frac{{\mu }_1^2{\sigma }_2^2+{\mu }_2^2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}-(\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}{)}^2}{\frac{2{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}& =\frac{({\mu }_1^2{\sigma }_2^2+{\mu }_2^2{\sigma }_1^2)({\sigma }_1^2+{\sigma }_2^2)+({\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2{)}^2}{2{\sigma }_1^2{\sigma }_2^2({\sigma }_1^2+{\sigma }_2^2)}\\ & =\frac{({\mu }_1-{\mu }_2{)}^2}{2({\sigma }_1^2+{\sigma }_2^2)}\end{array}$$

则我们可以将概率密度函数的乘积写为

$$\begin{array}{rl}{f}_1(x)f_2(x)& =\frac{1}{2\pi {\sigma }_1{\sigma }_2}\exp (-\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2}-\frac{(x-{\mu }_2{)}^2}{2{\sigma }_2^2})\\ & =\frac{1}{2\pi {\sigma }_1{\sigma }_2}\exp (-\frac{(x-\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}{)}^2}{\frac{2{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}-\frac{({\mu }_1-{\mu }_2{)}^2}{2({\sigma }_1^2+{\sigma }_2^2)})\\ & =\underset{S_g}{\underbrace{\frac{1}{\sqrt{2\pi ({\sigma }_1^2+{\sigma }_2^2)}}\exp (-\frac{({\mu }_1-{\mu }_2{)}^2}{2({\sigma }_1^2+{\sigma }_2^2)})}}\times \frac{1}{\sqrt{2\pi \frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}}\exp (-\frac{(x-\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}{)}^2}{\frac{2{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}})\\ & =S_g\times \frac{1}{\sqrt{2\pi \mu }}\exp (-\frac{(x-\mu {)}^2}{2\sigma })\end{array}$$

其中

$$\mu =\frac{{\mu }_2{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2},{\sigma }^2=\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}$$

所以两个高斯分布的乘积仍然为高斯分布，且均值为$\mu$，方差为${\sigma }^2$，$S_g$被称为缩放因子，即相乘后的分布函数为一个被压缩或者放大的高斯分布，相乘后的概率密度的积分不等于1，但其方差和均值性质不变，仍然符合高斯分布。

​ 拓展到多个高斯分布相乘的结果，可以得到

$$\mu =\frac{{\mu }_1{\sigma }_2^2{\sigma }_3^2+{\mu }_2{\sigma }_1^2{\sigma }_3^2+{\mu }_3{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2{\sigma }_2^2+{\sigma }_1^2{\sigma }_3^2+{\sigma }_2^2{\sigma }_3^2},{\sigma }^2=\frac{{\sigma }_1^2{\sigma }_2^2{\sigma }_3^2}{{\sigma }_1^2{\sigma }_2^2+{\sigma }_1^2{\sigma }_3^2+{\sigma }_2^2{\sigma }_3^2}$$

2. Code

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm# 设定均值和标准差
mean = np.array([1, 2, 3])
var = np.array([1, 3, 5])x = np.linspace(-15, 15, 1000)
pdfs = []
# 计算高斯分布的概率密度函数（Probability Density Function, PDF）
for mu, sigma in zip(mean, var):pdfs.append(norm.pdf(x, mu, np.sqrt(sigma)))# 绘制高斯分布曲线
plt.plot(x, pdfs[0], 'r-', linewidth=2, label='mean=1, var=1')
plt.fill_between(x, pdfs[0], color='red', alpha=0.5)
plt.plot(x, pdfs[1], 'g-', linewidth=2, label='mean=2, var=3')
plt.fill_between(x, pdfs[1], color='g', alpha=0.5)
plt.plot(x, pdfs[2], 'b-', linewidth=2, label='mean=3, var=5')
plt.fill_between(x, pdfs[2], color='b', alpha=0.5)# 计算三个高斯分布的乘积
prod_mean = 1.0 / np.sum(np.reciprocal(mean), axis=0)
prod_var = prod_mean * np.sum(mean / var, axis=0)
pdf = norm.pdf(x, prod_mean, np.sqrt(prod_var))
plt.plot(x, pdf, 'k--', linewidth=2, label='product')
plt.fill_between(x, pdf, color='y', alpha=0.7)# 添加标签和标题
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('Normal Distribution')
plt.legend()# 显示图形
plt.show()

Reference

https://blog.csdn.net/chaosir1991/article/details/106910668

这篇关于【Math】高斯分布的乘积 Product of Guassian Distribution【附带Python实现】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---