通量专题
SAP PI系统关于接口清单和接口通量的自定义视图
根据实际业务需要,在SAP PI系统上做了两个视图:一个是基于IC的接口清单,另一个是按照接口每日统计的接口通量(包括访问量、数据包大小)。将这两部分数据通过接口推送到第三方云平台上进行PO数据大屏的展示。 drop view gd_ic_list;/*创建intergrated configration List 视图 gd_IC_LIST*/create view gd
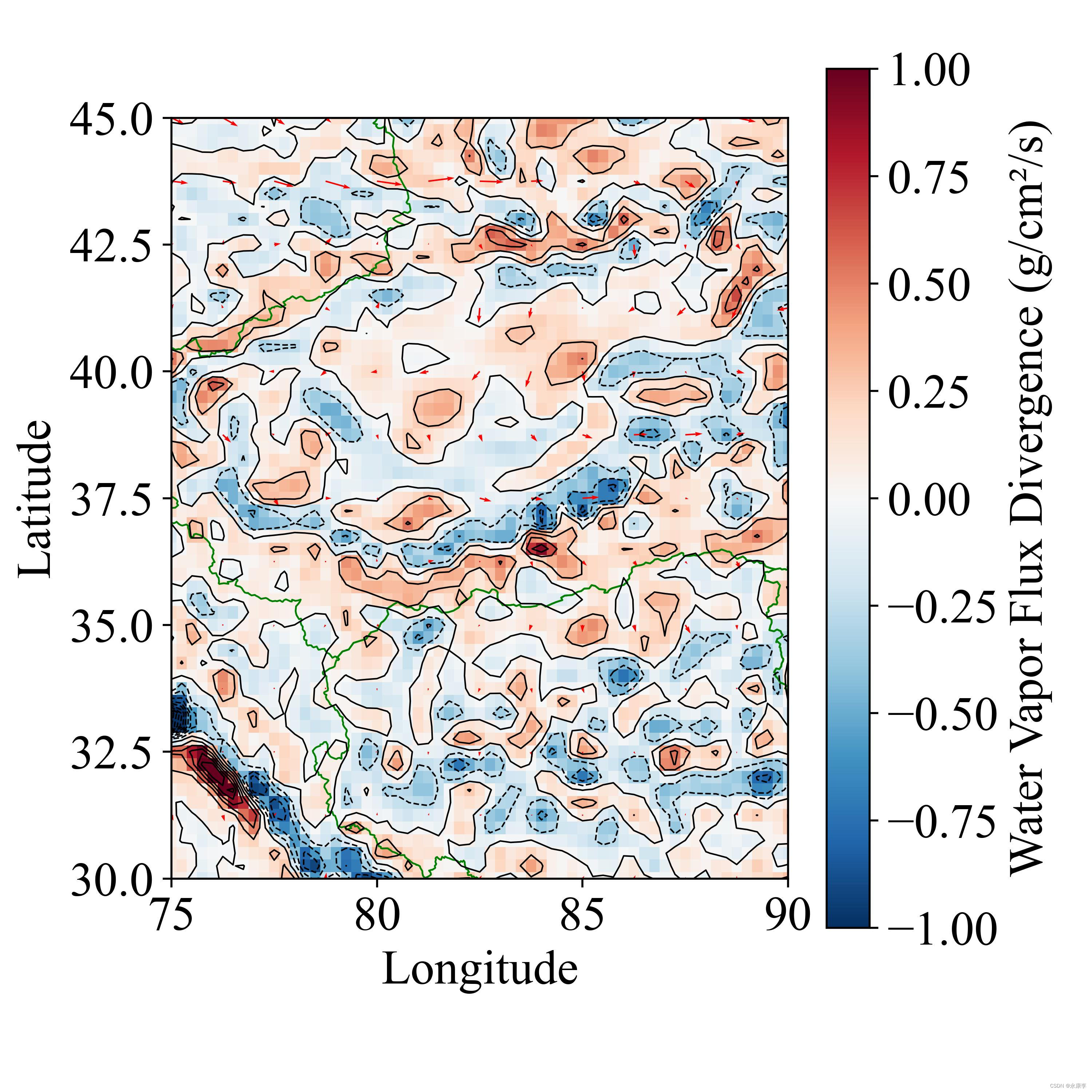
python ERA5 画水汽通量散度图地图:风速风向矢量图、叠加等高线、色彩分级、添加shp文件、添加位置点及备注
动机 有个同事吧,写论文,让我帮忙出个图,就写了个代码,然后我的博客好久没更新了,就顺便贴上来了! 很多人感兴趣风速的箭头怎样画,可能这种图使用 NCL 非常容易,很多没用过代码的小朋友,就有点犯怵,怕 python 画起来很困难。但是不然,看完我的代码,就会发现很简单,并且也可以批量,同时还能自定义国界等shp文件,这对于发sci等国际论文很重要,因为有时候内置的国界是有问题的。 数据 本
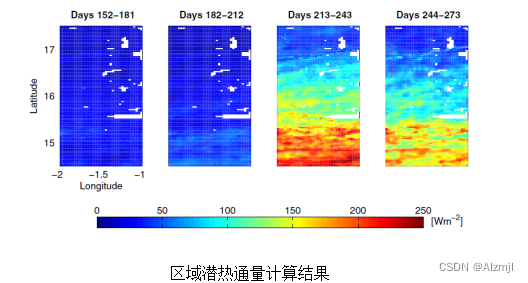
农田通量计算:从理论到实践的全方位指导
地表水热通量主要包括感热/显热通量和潜热通量,是陆-气交互以及水-热-碳循环研究的重要变量。其中,潜热通量是地表蒸散发的能量形式,对农业水资源管理、作物水分利用效率等非常关键。由于热红外遥感对地表干湿变化、以及农业干旱响应快速,利用地表温度遥感数据可以快速准确的反演地表水热通量。美国农业部(USDA)等也将这类方法作为农田通量计算的主流方法 目录 通量计算原理站点数据准备及模型调试区域数据
小身材大通量,米家净水器800G引领家庭净水首选
当“水健康”在当代消费者健康需求列表里脱颖而出,净水产品也就顺势成为新一代家居必备神器。 面对越来越卷的“净水”市场,全新升级上市的米家净水器800G打出“超小巧机身”“大屏智显龙头”“升级低音泵”三张王牌,致力于成为“家庭净水首选”。 9月20日,米家净水器800G开启预售,预售价1799元,建议零售价1999元。 净水两全法则:小机身、大容量 对想安装净水器但厨下空间有限的用户
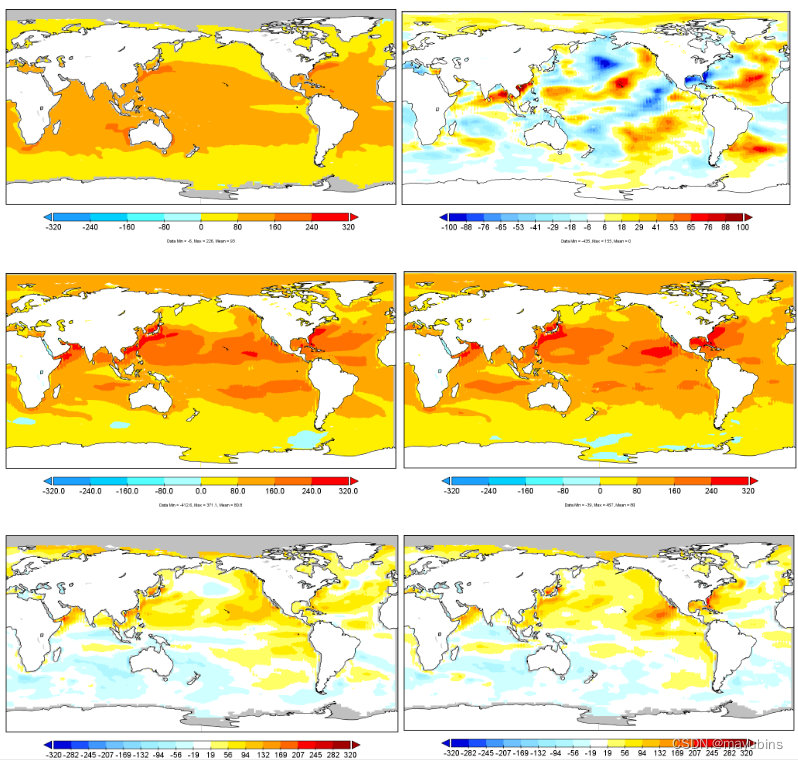
水汽稳定度修正函数\Psi_q对潜热通量影响--模式验证工作
我之前提出了一个水汽通量廓线关系,这项工作偏理论,如果对下面说的背景不了解的话可以看下 https://agupubs.onlinelibrary.wiley.com/share/YNSG74MV8B8BAAUMCHN3?target=10.1029/2022JD036708 那会没把提出的水汽稳定度修正函数加到CAS-ESM,当时对CAS-ESM模式还没这么熟悉,也想着师兄能帮我,但
空间连通区域@曲面积分为零问题@通量和散度@高斯公式物理意义
文章目录 沿任意闭曲面的曲面积分为0的条件空间连通区域概念小结例 充要条件定理证明 通量和散度流量(通量)例 散度和高斯公式的物理意义借助速度场讨论一般向量场的散度小结例 高斯公式的向量场的通量和散度向量形式 沿任意闭曲面的曲面积分为0的条件 与讨论曲线积分中闭曲线积分为0的问题类似,这里讨论曲面积分 ∬ Σ P d y d z + Q d z d x + R d x d
展讯UMS618 610全网通量产资料全方位解析
展讯UMS618 610全网通量产资料 展讯 618 610全网通4G全套量产软硬件资料及原厂硬件参考设计资料 标题:展讯UMS618 610全网通量产资料全方位解析 摘要:本文将对展讯UMS618 610全网通量产资料进行全方位的解析,从背景介绍、技术解析、应用场景等多个角度进行详细阐述,为相关领域的研究人员和技术人员提供有益的参考。 一、引言 随着全球通信市场的快速发展,网络通达性成
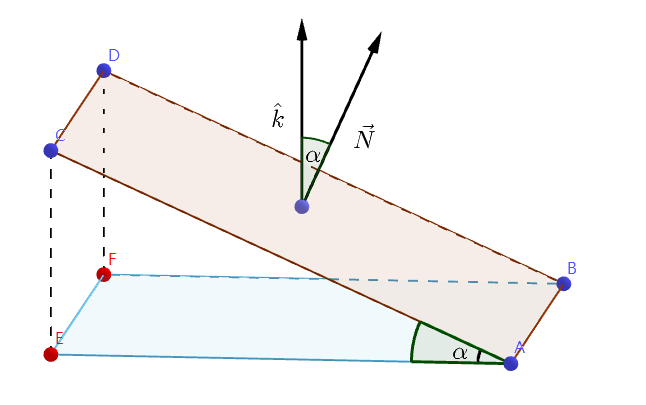
多变量微积分笔记17——通量
在流体运动中,通量是单位时间内流经某单位面积的某属性量,是表示某属性量输送强度的物理量。在大气科学中,包含动量通量、热通量、物质通量和水通量。 本章关于向量和点积的相关知识课参考《线性代数笔记3——向量2(点积)》。 通量 通量实际上是一种线积分。如果有一条平面曲线C和这个平面上的向量场F,通量用符号表示就是: 其中ds是曲线C的微元,n是垂直于ds的单位
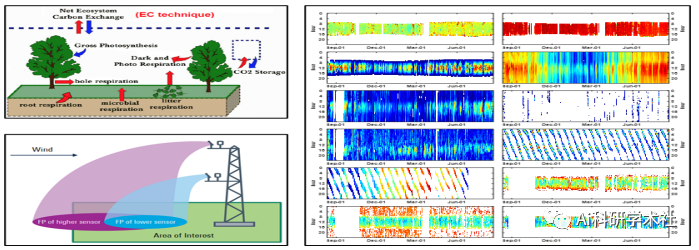
涡度通量数据处理技术
原文链接:基于MATLAB涡度通量数据处理实践技术应用 1、以涡度通量塔的高频观测数据为例:基于MATLAB开展上机操作 2、涡度通量观测基本概况:观测技术方法、数据获取与预处理等 3、涡度通量数据质量控制:通量数据异常值识别与剔除等 4、涡度通量数据缺失插补:结合气象数据进行通量数据缺失插补等 5、涡度通量数据组分拆分:计算生态系统呼吸和总初级生产力等 6、涡度通量数据可视化分