多变量微积分笔记17——通量

　　在流体运动中，通量是单位时间内流经某单位面积的某属性量，是表示某属性量输送强度的物理量。在大气科学中，包含动量通量、热通量、物质通量和水通量。

　　本章关于向量和点积的相关知识课参考《线性代数笔记3——向量2（点积）》。

通量

　　通量实际上是一种线积分。如果有一条平面曲线C和这个平面上的向量场F，通量用符号表示就是：

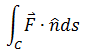
　　其中ds是曲线C的微元，n是垂直于ds的单位法向量（按C的方向顺时针旋转90°）:

　　如果把F看成一个流速场，比如水流正在以某种速度流动，那么F解释了在平面上每一点的水流流动情况。处于F中的曲线C的通量度量了单位时间内有多少流体流过曲线C。可以将F看成河流，C是位于河中的渔网，通量可以计算单位时间内有多少河水流过了渔网。

　　如下图所示，ΔS是匀速场中曲线的一小段：

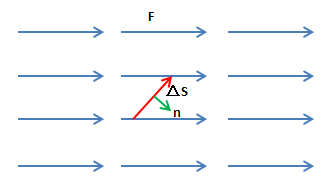
　　在单位时间后，通过ΔS的水流将是一个平行四边形：

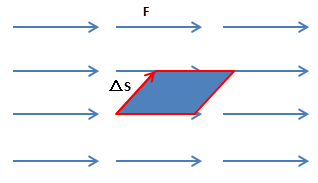
　　已知平行四边形的一边ΔS，另一边由F表示，如果用ΔS作底，那么平行四边形的面积：

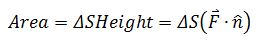
　　如果流体不是匀速的，需要取足够小的单位时间。将所有流过ΔS的水流做积分，就是单位时间内通过C的水流的净流量，即C的通量。如果流体从左到右通过C，通量取正值；反之取负值。

　　对比线积分的定义，

　　在线积分中，F与T的点积表示F在T方向的分量，T与ds同向，线积分度量的是在场中沿曲线前进F做的功，或者说克服F做了多少功；在通量中，F与n的点积表示F在 n方向的分向量，n与ds垂直，通量度量的是有多少向量场会通过曲线，正负号表示通量的方向。

通量的计算

几何方法

　　如下图所示，曲线C是半径为a，圆心在原点的圆，求C在场中的通量。

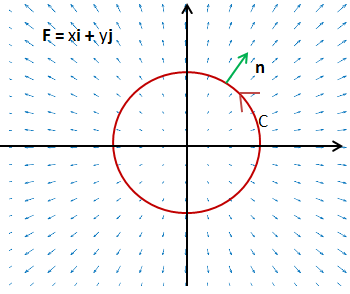
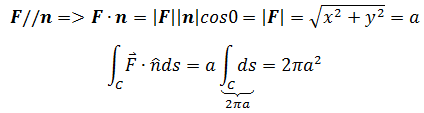
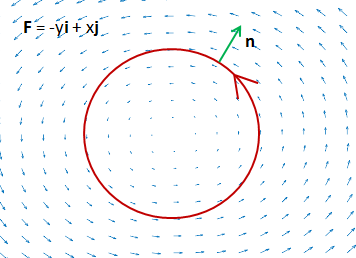
　　如果C在F = -yi + xj中，则n⊥F，二者的点积是0，通量也是0，因为水流绕着C流动，并没有流过C。

线积分法

　　我们将上一节的计算方法称为几何法，这对简单的通量很有效，但事实上曲线C往往很复杂，这就需要一种常规的方法。既然通量的表达式与线积分相似，就可以尝试用线积分计算通量。

　　在线积分中：

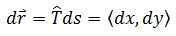
　　T 是ds同向的单位向量。对比通量，n是ds的法向量（将T顺时针旋转90°），所以：

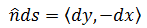
　　现在可以总结通量的计算公式，如果向量场F = <M,N>：

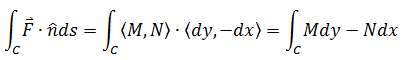
　　在物理解释上，通量和线积分描述了不同的度量，但是在计算上，二者没有什么实质性区别。

格林公式

　　如果是在处处有定义且处处可导的平面向量场F = <M,N>中求逆时针方向闭合曲线C的通量，就可以和线积分一样，使用格林公式。

　　与上一篇的线积分不同，通量是求F在ds法向量方向分量的积分，所以上面的公式也被称为格林公式的正交形式，它是格林公式的另一种表达。

公式的证明

散度

　　这里的div(F)就是散度，它度量的是流体的发散程度。现在，格林公式可以写成：

示例

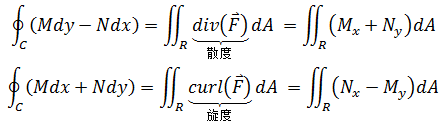
　　曲线C是逆时针方向半径为a的圆，求C在场F = xi + yj中的通量。

综合示例

示例1

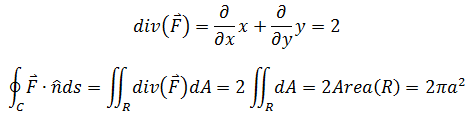
　　计算通量

　　a) F = 3<1, 1>,C from (0,0) to (1,1)

　　a) F = 3< -1, 1>,C from (0,0) to (1,1)

　　a)

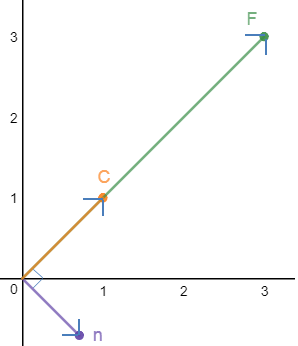
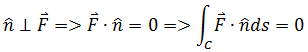
　　b)

示例2

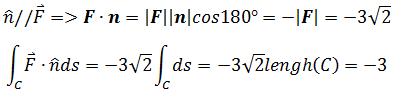
　　计算向量场F = <x, y>中C的通量，C由单位半圆和x轴上的线段围成，如下图所示：

　　方法1：使用格林公式

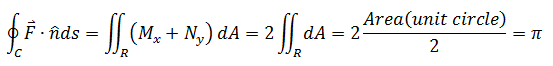
　　方法2：使用线积分

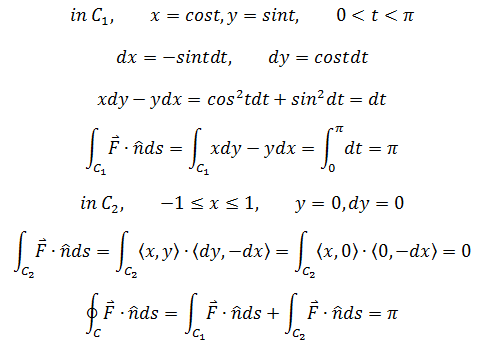
作者：我是8位的