本文主要是介绍三维向量场中的通量,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.空间向量场
在空间的每一个点,都有 F → = P i ^ + Q j ^ + R k ^ \overrightarrow{F}=P\widehat{i}+Q\widehat{j}+R\widehat{k} F=Pi +Qj +Rk
其中 P P P, Q Q Q, R R R,均为 x x x, y y y, z z z的函数
2.流量
在2维中,向量场穿过曲线C的流量记为
∫ C F → ⋅ n ^ d s \int_C{\overrightarrow{F}\cdot \widehat{n}\ ds} ∫CF⋅n ds
在3维中,向量场穿过曲面S的流量记为
∬ S F → ⋅ n ^ d S \iint_S{\overrightarrow{F}\cdot \widehat{n}\ dS} ∬SF⋅n dS
为了方便表示,记 d S → = n ^ d S d\overrightarrow{S}=\widehat{n}\ dS dS=n dS
3.将 d S → d\overrightarrow{S} dS转换为 d x d y dxdy dxdy
(1)曲面显示表示为 z = f ( x , y ) z=f(x,y) z=f(x,y)
如图所示,假设曲面 z = f ( x , y ) z=f(x,y) z=f(x,y)上一小块 Δ S \Delta S ΔS在xoy轴上的投影为矩形ABCD,由于取的块足够小,可以将其视为平行四边形。
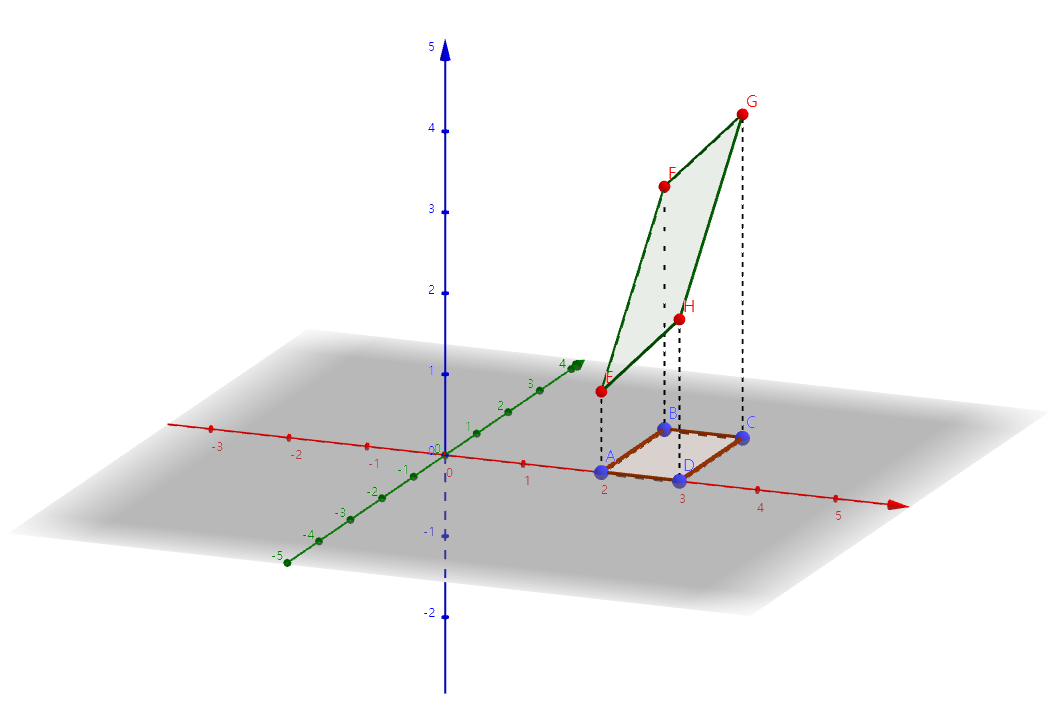
矩形 A D AD AD的长度为 Δ x \Delta x Δx(x的变化量), A B AB AB的长度为 Δ y \Delta y Δy(y的变化量)
设 E E E点坐标为 ( x , y , f ( x , y ) ) (x,y,f(x,y)) (x,y,f(x,y)),则 F F F点坐标为 ( x , y + Δ y , f ( x , y + Δ y ) ) (x,y+\Delta y,f(x,y+\Delta y)) (x,y+Δy,f(x,y+Δy)),其中 f ( x , y + Δ y ) f(x,y+\Delta y) f(x,y+Δy)可以使用线性近似,即 f ( x , y + Δ y ) ≈ f ( x , y ) + Δ y ⋅ f y ′ f(x,y+\Delta y)\approx f(x,y)+\Delta y\cdot f_y^\prime f(x,y+Δy)≈f(x,y)+Δy⋅fy′,则 F F F点坐标为 ( x , y + Δ y , f ( x , y ) + Δ y ⋅ f y ′ ) (x,y+\Delta y,f(x,y)+\Delta y\cdot f_y^\prime) (x,y+Δy,f(x,y)+Δy⋅fy′),同理可得 H H H点的坐标为 ( x + Δ x , y , f ( x , y ) + Δ x ⋅ f x ′ ) (x+\Delta x,y,f(x,y)+\Delta x\cdot f_x^\prime) (x+Δx,y,f(x,y)+Δx⋅fx′),则
E F → = ( 0 , Δ y , Δ y ⋅ f y ′ ) \overrightarrow{EF}=\left( 0,\Delta y,\Delta y\cdot f_y' \right) EF=(0,Δy,Δy⋅fy′)
E H → = ( Δ x , 0 , Δ x ⋅ f x ′ ) \overrightarrow{EH}=\left( \Delta x,0,\Delta x\cdot f_x' \right) EH=(Δx,0,Δx⋅fx′)
Δ S → = E F → × E H → = ∣ i ^ j ^ k ^ 0 Δ y Δ y ⋅ f y ′ Δ x 0 Δ x ⋅ f x ′ ∣ = ( Δ x Δ y ⋅ f x ′ , Δ x Δ y ⋅ f y ′ , − Δ x Δ y ) = ( f x ′ , f y ′ , − 1 ) Δ x Δ y \Delta \overrightarrow{S}=\overrightarrow{EF}\times \overrightarrow{EH}=\left| \begin{matrix} \widehat{i}& \widehat{j}& \widehat{k}\\ 0& \Delta y& \Delta y\cdot f_y'\\ \Delta x& 0& \Delta x\cdot f_x'\\ \end{matrix} \right|=\left( \Delta x\Delta y\cdot f_x',\Delta x\Delta y\cdot f_y',-\Delta x\Delta y \right) =\left( f_x',f_y',-1 \right) \Delta x\Delta y ΔS=EF×EH=∣∣∣∣∣∣i 0Δxj Δy0k Δy⋅fy′Δx⋅fx′∣∣∣∣∣∣=(ΔxΔy⋅fx′,ΔxΔy⋅fy′,−ΔxΔy)=(fx′,fy′,−1)ΔxΔy
(说明: ∣ E F → × E H → ∣ \left| \overrightarrow{EF}\times \overrightarrow{EH} \right| ∣∣∣EF×EH∣∣∣为平行四边形EFGH的面积, E F → × E H → \overrightarrow{EF}\times \overrightarrow{EH} EF×EH的方向为平面EFGH的法向量方向)
所以
d S → = ± ( f x ′ , f y ′ , − 1 ) d x d y d\overrightarrow{S}=\pm \left( f_x',f_y',-1 \right) dxdy dS=±(fx′,fy′,−1)dxdy
正负号取决于取哪面为正方向。
(2)参数化曲面
假设可以将曲面 S S S用 u u u, v v v两个变量表示,即 { x = x ( u , v ) y = y ( u , v ) z = z ( u , v ) \left\{ \begin{array}{l} x=x\left( u,v \right)\\ y=y\left( u,v \right)\\ z=z\left( u,v \right)\\ \end{array} \right. ⎩⎨⎧x=x(u,v)y=y(u,v)z=z(u,v) 则位置矢量 r → = r → ( u , v ) \overrightarrow{r}=\overrightarrow{r}\left( u,v \right) r=r(u,v)。
考虑与参数 Δ u \Delta u Δu和 Δ v \Delta v Δv的变化对应的曲面。
由于 Δ u \Delta u Δu和 Δ v \Delta v Δv较小,所以可以将曲面视为平行四边形,其两条边分别为 ∂ r → ∂ u Δ u \frac{\partial \overrightarrow{r}}{\partial u}\Delta u ∂u∂rΔu和 ∂ r → ∂ v Δ v \frac{\partial \overrightarrow{r}}{\partial v}\Delta v ∂v∂rΔv
所以
Δ S → = ± ( ∂ r → ∂ u Δ u ) × ( ∂ r → ∂ v Δ v ) \Delta \overrightarrow{S}=\pm \left( \frac{\partial \overrightarrow{r}}{\partial u}\Delta u \right) \times \left( \frac{\partial \overrightarrow{r}}{\partial v}\Delta v \right) ΔS=±(∂u∂rΔu)×(∂v∂rΔv)
所以
d S → = ± ( ∂ r → ∂ u × ∂ r → ∂ v ) d u d v d\overrightarrow{S}=\pm \left( \frac{\partial \overrightarrow{r}}{\partial u}\times \frac{\partial \overrightarrow{r}}{\partial v} \right) dudv dS=±(∂u∂r×∂v∂r)dudv
正负号取决于取哪面为正方向。
(3)曲面隐式表示为 g ( x , y , z ) = 0 g(x,y,z)=0 g(x,y,z)=0
曲面的法向量 N → = ∇ g \overrightarrow{N}=\nabla g N=∇g。
取一小块倾斜的曲面(其中一条边水平,并且取的足够小可以看做一小块平面),设取的曲面与水平面 x o y xoy xoy的夹角为 α \alpha α,如图所示。
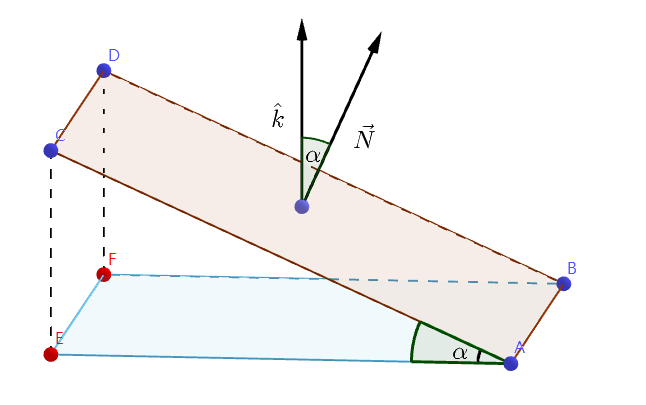
则曲面面积 Δ S \Delta S ΔS与在 x o y xoy xoy轴上的投影的面积 Δ A \Delta A ΔA关系为
Δ S ⋅ cos α = Δ A \Delta S\cdot \cos \alpha =\Delta A ΔS⋅cosα=ΔA
(注,此处不写为 Δ x Δ y \Delta x \Delta y ΔxΔy是因为投影的两条边不一定和x轴或y轴平行)
由于
cos α = k ^ ⋅ N → ∣ k ^ ∣ ⋅ ∣ N → ∣ = k ^ ⋅ N → ∣ N → ∣ \cos \alpha =\frac{\widehat{k}\cdot \overrightarrow{N}}{\left| \widehat{k} \right|\cdot \left| \overrightarrow{N} \right|}=\frac{\widehat{k}\cdot \overrightarrow{N}}{\left| \overrightarrow{N} \right|} cosα=∣∣∣k ∣∣∣⋅∣∣∣N∣∣∣k ⋅N=∣∣∣N∣∣∣k ⋅N
则
d S = ∣ N → ∣ k ^ ⋅ N → d A dS=\frac{\left| \overrightarrow{N} \right|}{\widehat{k}\cdot \overrightarrow{N}}\ dA dS=k ⋅N∣∣∣N∣∣∣ dA
n ^ d S = ∣ N → ∣ n ^ k ^ ⋅ N → d A = ± N → k ^ ⋅ N → d A = ± N → k ^ ⋅ N → d x d y \widehat{n}dS=\frac{\left| \overrightarrow{N} \right|\widehat{n}}{\widehat{k}\cdot \overrightarrow{N}}\ dA=\pm \frac{\overrightarrow{N}}{\widehat{k}\cdot \overrightarrow{N}}\,\,dA=\pm \frac{\overrightarrow{N}}{\widehat{k}\cdot \overrightarrow{N}}\,\,dxdy n dS=k ⋅N∣∣∣N∣∣∣n dA=±k ⋅NNdA=±k ⋅NNdxdy
正负号取决于取哪面为正方向。
4.散度定理(高斯公式)
如果 S S S是区域 D D D的闭合曲面,曲线法向量方向向外,并且向量 F ⃗ \vec{F} F在区域D内有定义且可微,则
∬ S F → ⋅ d S → = ∭ D d i v ( F → ) d V , 其中 d i v ( F → ) = ( P x + Q y + R z ) \iint_S{\overrightarrow{F}\cdot d\overrightarrow{S}}=\iiint_D{div\left( \overrightarrow{F} \right) dV}\ ,\ \text{其中\ }div\left( \overrightarrow{F} \right) =\left( P_x+Q_y+R_z \right) ∬SF⋅dS=∭Ddiv(F)dV , 其中 div(F)=(Px+Qy+Rz)
这篇关于三维向量场中的通量的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








