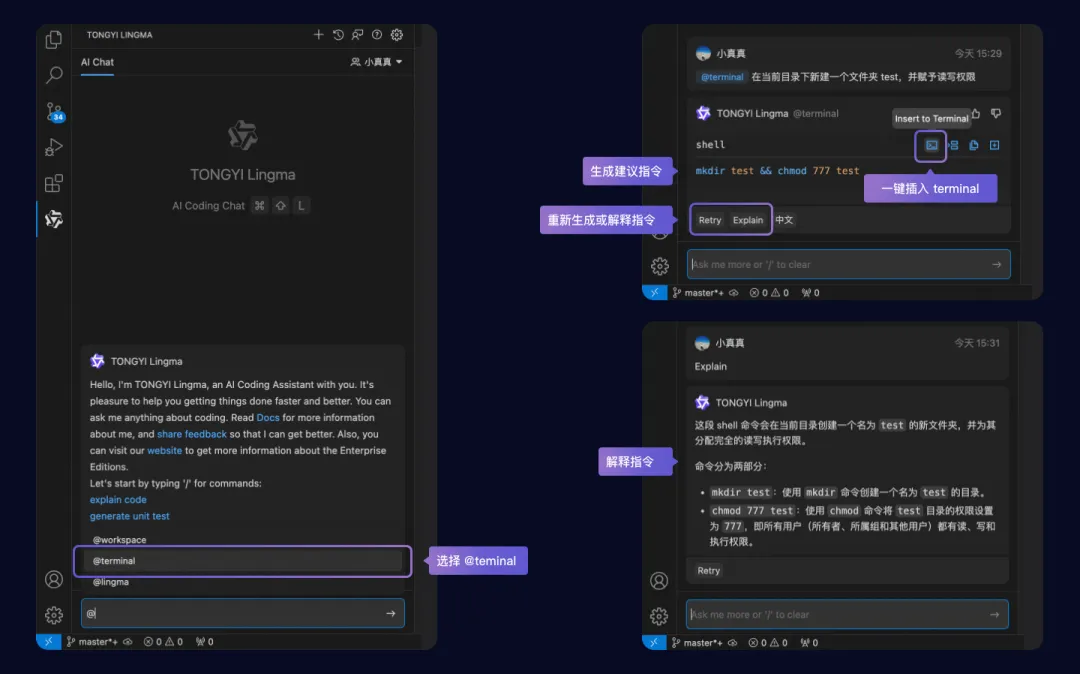
通义专题
通义灵码助力高校开学第一课,“包”你满意,新学期加油!
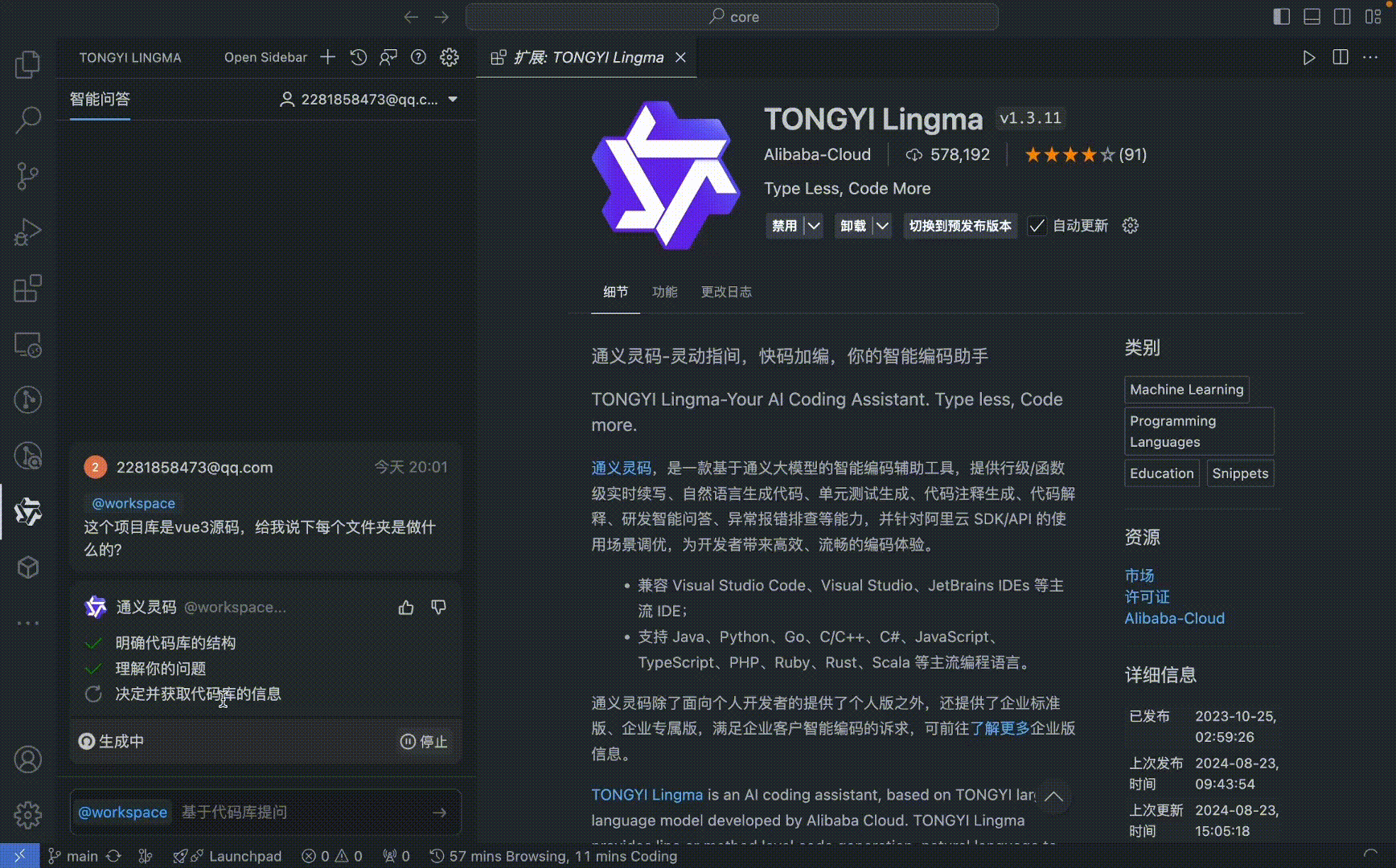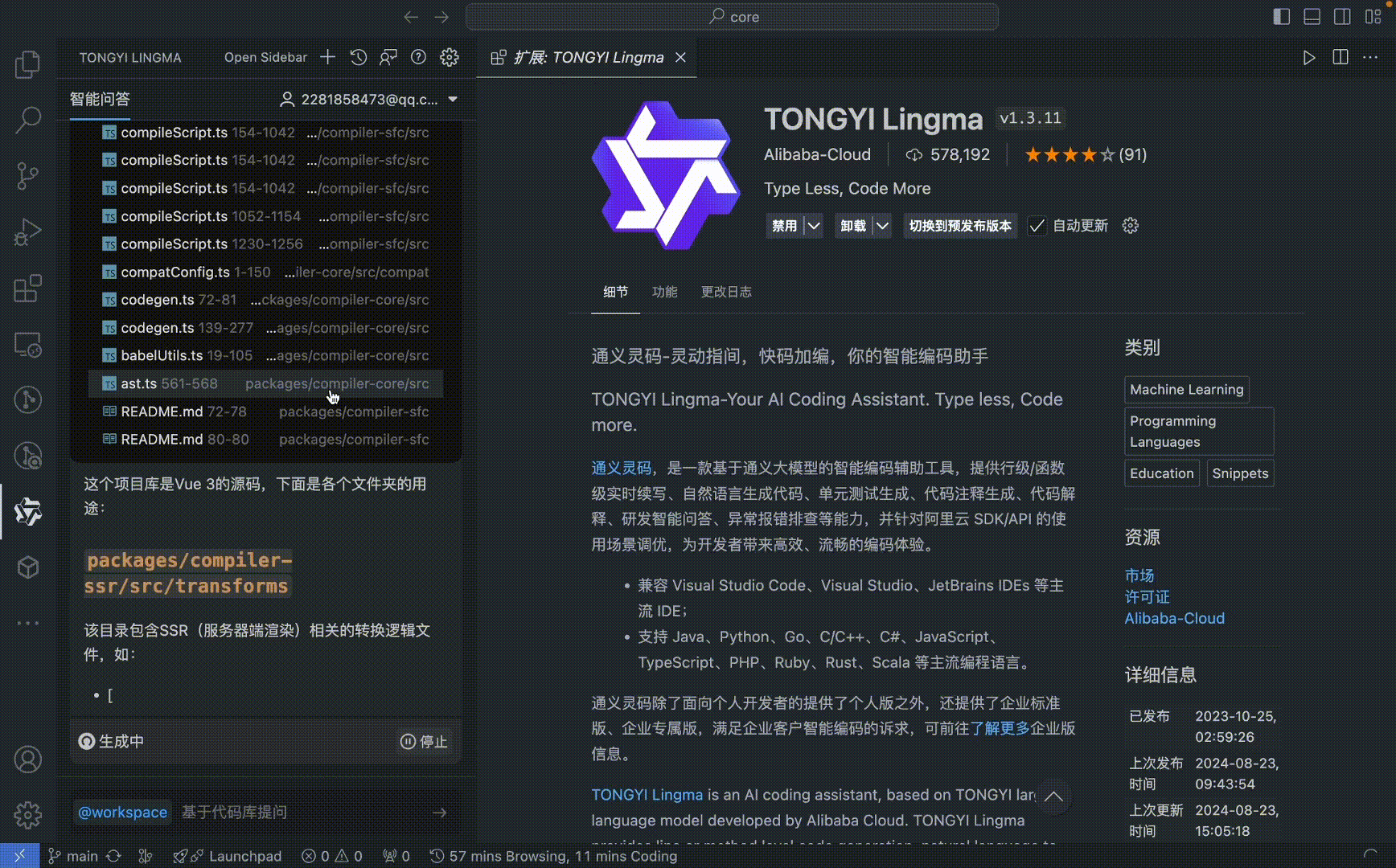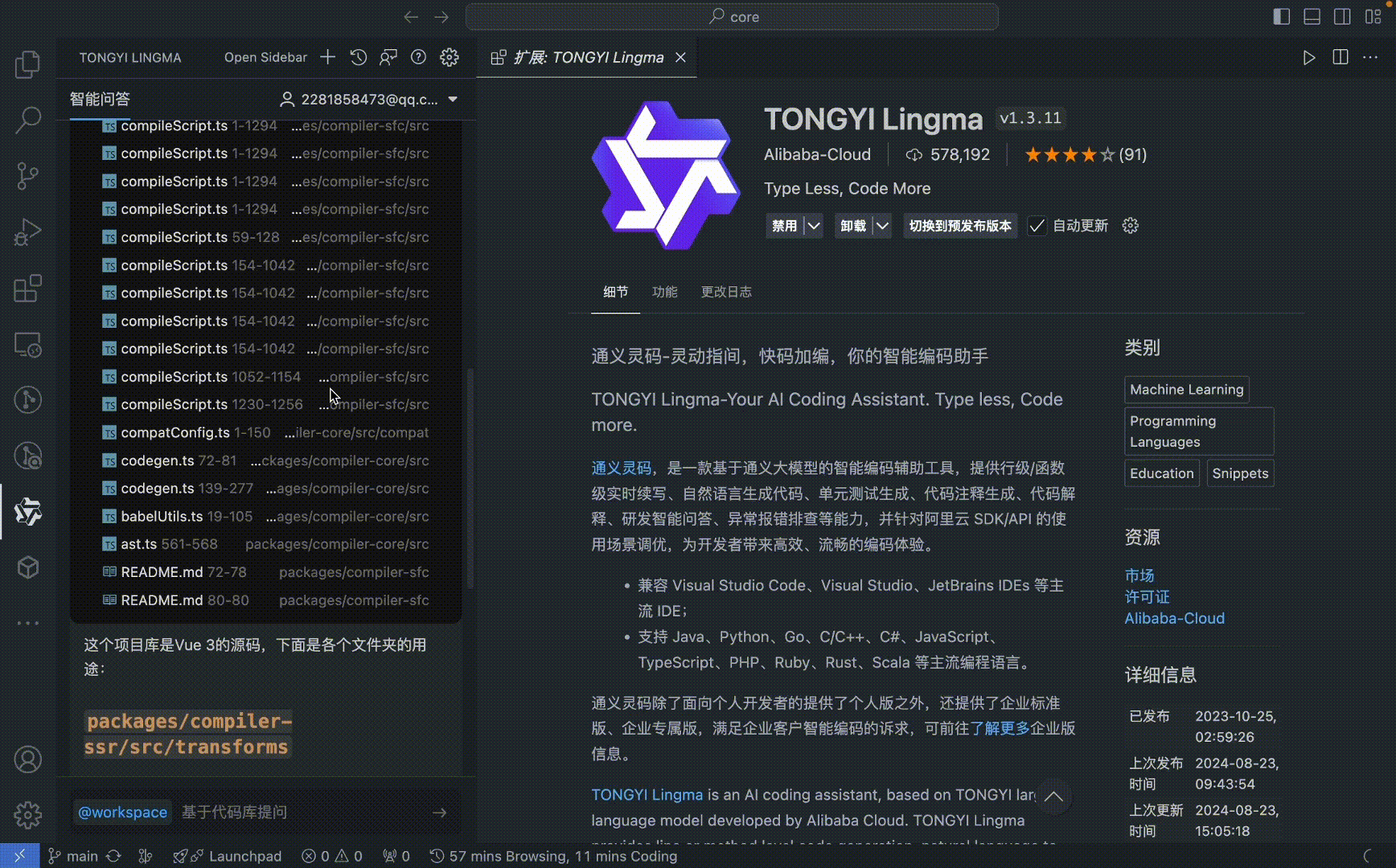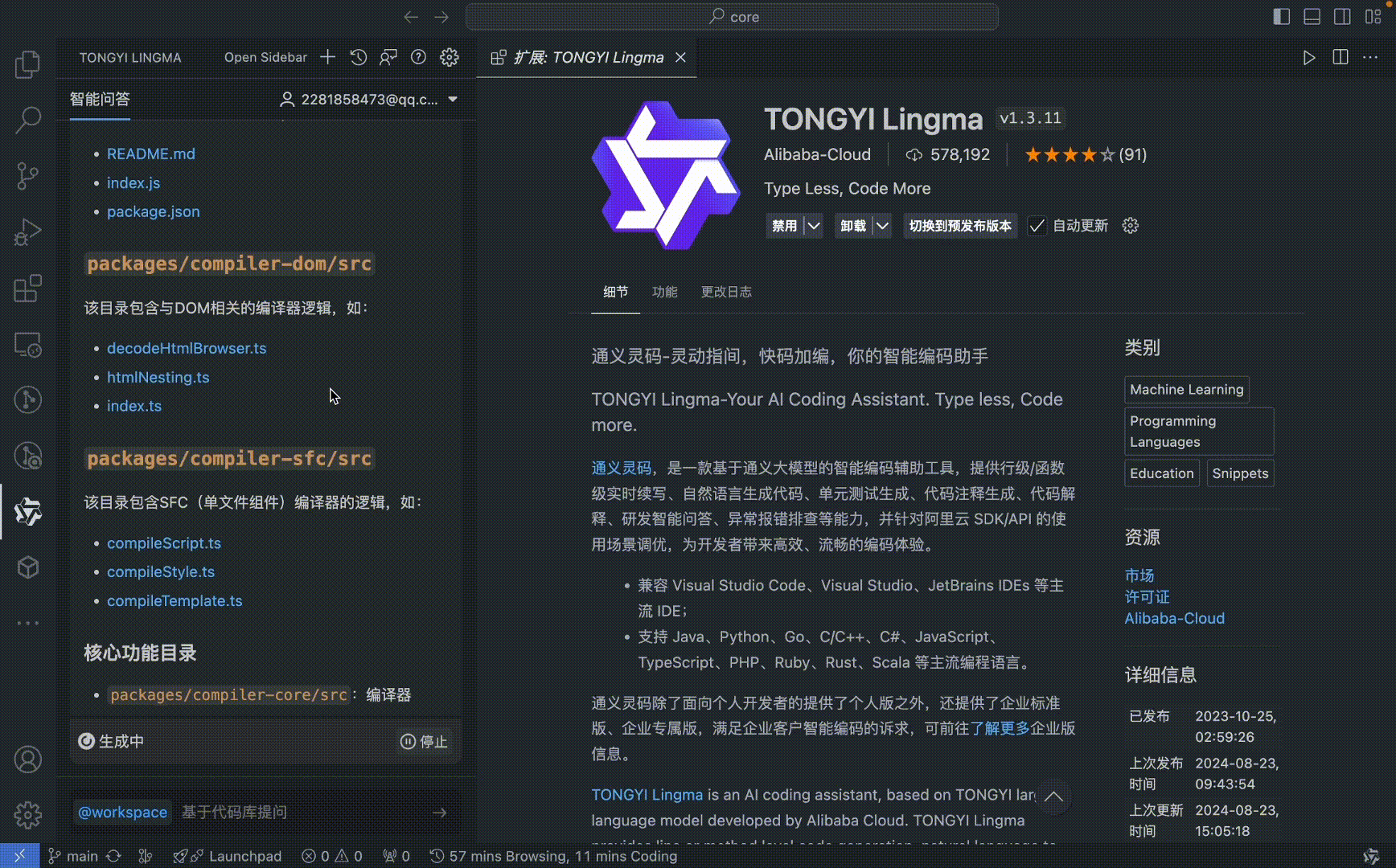
通义灵码作为国内领先的 AI 编码工具,近年来在高校中得到了广泛应用和推广。它不仅帮助大学生更高效地学习编程、提高代码质量,还激发了他们的创新思维,并为未来的职业生涯做好了准备。 通义灵码是什么? 通义灵码是一款基于通义大模型的智能编码助手,可以在你进行编码工作时,为你提供代码实时续写、注释生成代码、单元测试生成、代码优化、注释生成、代码解释、研发智能问答、代码问题修复等辅助编码工作的功能
通义千问Qwen 2大模型的预训练和后训练范式解析
LLMs,也就是大型语言模型,现在已经发展得挺厉害的。记得最开始的时候,我们只有GPT这样的模型,但现在,我们有了一些更复杂的、开放权重的模型。以前,训练这些模型的时候,我们主要就是做预训练,但现在不一样了,我们还会加上后训练这个阶段。 咱们今天就以通义千问Qwen 2这个模型为例,来好好分析一下Qwen 2的预训练和后训练都是怎么搞的。它在大型语言模型界里算是挺能打的。不过,虽然它很强
体验通义灵码 @workspace:轻松分析项目结构,结合代码仓库理解工程、查询问答等
国际市场研究机构 Gartner 发布业界首个 AI 代码助手魔力象限,阿里云进入挑战者象限。通义灵码在产品功能和市场应用等方面表现位列国际前列,在国内同类产品中排名第一。在关键能力评分中,通义灵码在代码生成、代码解释、代码调试等多项能力领先,其中代码解释能力位列全球第二。 这也是国产 AI 编码工具目前取得的最高成绩! 近期,通义灵码上线新能力:@workspace,基于本地代码库的 RAG
通义千问AI PPT初体验:一句话、万字文档、长文本一键生成PPT!
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,专注于分享AI全维度知识,包括但不限于AI科普,AI工具测评,AI效率提升,AI行业洞察。关注我,AI之路不迷路,2024我们一起变强。 你有多久没有听到国内AI大模型的最新消息了? 不是国内AI领域不卷了,而是“卷”的方向变了。2023年卷
通义说【线性代数】什么是线性
线性关系是一种简单的数学关系,其中因变量(dependent variable)相对于自变量(independent variable)的变化率是常数,这意味着随着自变量的增加,因变量按照固定的比例增加或减少。这种关系可以用直线来表示。 线性函数具有以下性质: 叠加原理:两个线性函数的和仍然是线性的。齐次性:线性函数满足齐次性原则,即如果一个函数是线性的,那么这个函数的输出应当与输入成比例。无
怎么在Windows操作系统部署阿里开源版通义千问(Qwen2)
怎么在Windows操作系统部署阿里开源版通义千问(Qwen2) | 原创作者/编辑:凯哥Java | 分类:人工智能学习系列教程 添加图片注释,不超过 140 字(可选) GitHub上qwen2截图 随着人工智能技术的不断进步,阿里巴巴通义千问团队近期发布了Qwen2系列开源模型,这一系列模型在多个领域展现出卓越的性能,特别是在自然语言理解、知识、代码、数学及多语言等能
通义说【流式读取】连续方式读取文件
在 Python 中,通过流的方式读取文件是一种高效处理大数据的方法,尤其是在处理大型文件时。流式读取允许程序按部分读取和处理文件,而不是一次性将整个文件加载到内存中。这种方式特别适用于处理那些文件大小远远超过可用内存的情况。 流式读取文件的意义 内存管理:避免一次性加载整个文件到内存中,从而节省内存资源。性能优化:对于大型文件,按需读取可以减少不必要的数据加载,提高程序的响应速度。错误恢复:
通义说【python】f-string
在Python中,f-string(格式化字符串)是一种在字符串字面量前加上f或F前缀的方式来创建字符串,它允许你在字符串中直接内嵌表达式。f-string是从Python 3.6版本(即Python 3.6及以后版本)开始引入的新特性。 f-string中的表达式会被替换为它们的值,这使得字符串格式化变得更加简洁和直观。表达式是写在花括号 {} 中的,这些表达式可以是变量名、更复杂的表达式或者
通义说【线性代数】线性方程组和线性代数的关系
线性方程组和线性代数之间有非常紧密的关系。事实上,线性方程组是线性代数的一个核心主题,而线性代数提供了解决线性方程组的一系列理论和工具。 线性方程组 线性方程组是由一组线性方程构成的集合,每个方程都表示未知变量的线性组合等于一个常数项。一个典型的线性方程组可以写作: a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 +
通义说【线性代数】为什么矩阵乘以向量是一个对矩阵中列向量的线性组合
矩阵乘以向量可以被理解为该向量在矩阵所代表的空间变换下的映射结果,也可以看作是矩阵列向量的线性组合。为了更好地理解这一点,让我们从矩阵乘法的基本定义出发。 假设有一个 m × n m \times n m×n的矩阵 A A A和一个 n n n维列向量 x \mathbf{x} x,矩阵 A A A可以写成由它的列向量组成的集合,即: A = [ a 1 , a 2 , … , a n ]
阿里 “通义灵码” 真的 “灵吗”,全保姆级实操
最近很多朋友,都在关注阿里公测的“通义灵码”,我索性也安装了,准备看看它真的有说的那么“灵吗”? 一、安装 官网:https://tongyi.aliyun.com/lingma/ 安装方式:https://tongyi.aliyun.com/lingma/download 帮助手册:https://help.aliyun.com/document_detail/2590613.ht
通义千问-VL-Chat-Int4
Qwen-VL 是阿里云研发的大规模视觉语言模型(Large Vision Language Model, LVLM)。Qwen-VL 可以以图像、文本、检测框作为输入,并以文本和检测框作为输出。Qwen-VL 系列模型性能强大,具备多语言对话、多图交错对话等能力,并支持中文开放域定位和细粒度图像识别与理解。 安装要求 (Requirements) python 3.8及以上版本pytor
关于springboot对接通义千问大模型的尝试
今天正在路上刷手机,突然看到群里有人发了一个链接,内容是Spring Cloud Alibaba AI 的使用,spring cloud AI的使用,于是就想着玩一玩试试,难度不大,就是有些文档的坑,这里做一个记录,后续会继续更新这个系列的,毕竟AI时代,我们springer也得搭一下顺风车。 一、文档阅读 我们看到文档其实描述了他的能力如下图,但是我们这里只尝试一下文生文的能力,其实说人话就
SpringBoot调用通义千问
提示:今日花了2个小时搞定了一个简易版的AI对话功能 文章目录 目录 文章目录 SpringBoot代码 引入库 controller 返回对象类 工具类 前端代码 编辑 效果展示 后端返回 SpringBoot代码 当然我只做了一个简易版的AI对话,你可以在我的基础之上进行改动 引入库 <dependency><group
【云故事探索】NO.7:「越用越上瘾」,中华财险 60% 研发人员用通义灵码提效
云布道师 中华联合财产保险股份有限公司运用“云+大模型”技术革新业务,通过阿里云的通义灵码大幅提升编码效率,近60%的研发人员采用,采纳的生成代码占比约20%,显著提升了团队创新能力与代码质量,并积极探索大模型在更多垂直业务场景的应用。 保险业被看成是社会“稳定器”和经济“助推器”,近年来已驶入数字化发展快车道。在 AI、大模型当道的今天,保险行业的研发流程、产品设计、场景拓展等业务链条各
关于springboot对接通义千问大模型的尝试(一)
今天正在路上刷手机,突然看到群里有人发了一个链接,内容是Spring Cloud Alibaba AI 的使用,spring cloud AI的使用,于是就想着玩一玩试试,难度不大,就是有些文档的坑,这里做一个记录,后续会继续更新这个系列的,毕竟AI时代,我们springer也得搭一下顺风车。 一、文档阅读 我们看到文档其实描述了他的能力如下图,但是我们这里只尝试一下文生文的能力,其实说人话就
《通义千问AI落地—下》:WebSocket详解
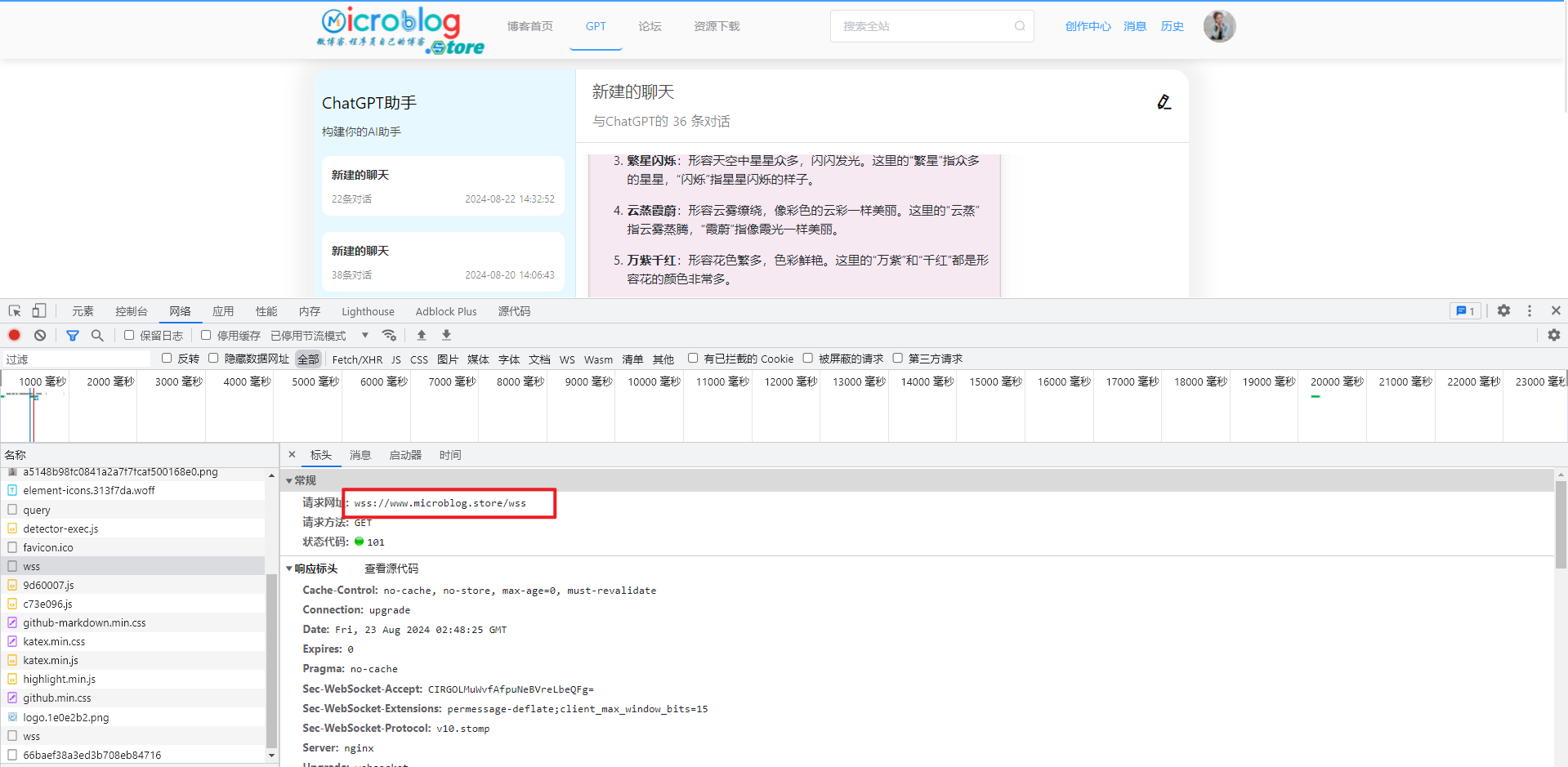
一、前言 文本源自 微博客 且已获授权,请尊重版权。 《通义千问AI落地——下篇》如约而至。Websocket在这一类引用中,起到前后端通信的作用。因此,本文将介绍websocket在这类应用场景下的配置、使用、注意事项以及ws连接升级为wss连接等;如下图,本站已经使用了wss连接: 二、后端接口 后端接口主要涉及Websocket的配置、握手认证、消息
【教学类65-02】20240622秘密花园涂色书02(通义万相)(A4横版2张,一大 68张纸136份)
背景需求 【教学类65-01】20240622秘密花园涂色书01(通义万相)(A4横版2张,一大3小 38张纸76份)-CSDN博客文章浏览阅读118次。【教学类65-01】20240622秘密花园涂色书01(通义万相)(A4横版2张,一大3小 38张纸76份)https://blog.csdn.net/reasonsummer/article/details/139899797 以上
【教学类-36-09】20240622钓鱼(通义万相)-A4各种大小的鱼
背景需求: 用通义万相获得大量的简笔画鱼的图片,制作成不同大小,幼儿用吸铁石钓鱼的纸片(回形针),涂色、排序等 补一张通义万相的鱼图 素材准备 (一)优质的鱼图片 (二)剔除的鱼(两个眼睛、很多鱼鳍、不是鱼的造型) (三)模板 模板4条(14.2*7.9) 模板9条(9.5*5.23) 模板10条(9.66*5.62)
【AI应用探讨】— 通义千问模型应用场景
目录 一、文字创作 二、文本处理 三、编程辅助 四、翻译服务 五、对话模拟 六、数据可视化 七、电商行业应用 八、教育行业应用 九、开发者与科研工作者应用 一、文字创作 故事、公文、邮件撰写:通义千问能够基于用户的指令和需求,生成符合要求的文本内容,如创作故事、撰写公文或邮件等。剧本、诗歌创作:其强大的文本生成能力也为文艺创作者提供了便利,如辅助创作剧本、诗歌等。
【AI原理解析】— 通义千问模型
目录 1. 技术基础与架构 自然语言处理技术(NLP) 知识图谱 超大规模语言模型 2. 原理与工作流程 输入解析 问题匹配与推理 答案生成 3. 技术特点与优势 高效性 多语言能力 可扩展性 4. 应用场景 1. 技术基础与架构 自然语言处理技术(NLP) 通义千问利用自然语言处理技术,包括文本分类、意图识别、命名实体识别等,来理解和解析用户输入的
【AI】通义千问使用指南:让你快速上手,成为问题解决高手!
大家好,我是木头左。 近日,继文心一言和讯飞星火之后,阿里虽迟但到,直接宣布开源两款“通义千问”大模型。作为国内首个开源且可商用的人工智能大模型,这会给我们带来哪些变化呢? 如何申请阿里通义千问? 本文将详细介绍如何在阿里通义千问申请账号,如以下步骤操作: 步骤1:下载阿里通义千问APP或访问PC端 访问https://qianwen.aliyun.com/,或搜索“阿里通义千问”
通义千问AI+Java
如何提问 Prompt的组成 角色:给 AI 定义一个最匹配任务的角色,比如:「你是一位软件工程师」「你是一位小学老师」指示:对任务进行描述上下文:给出与任务相关的其它背景信息(尤其在多轮交互中)例子:必要时给出举例,[实践证明其对输出正确性有帮助]输入:任务的输入信息;在提示词中明确的标识出输入输出:输出的格式描述,以便后继模块自动解析模型的输出结果,比如(JSON、Java) 先定义角
【教学类-12-12】20240617通义万相-动物图片6张编故事(A4一页4条)
背景需求 【教学类-12-11】20240612通义万相-动物图片连连看(A4一页3套)-CSDN博客文章浏览阅读891次,点赞34次,收藏11次。【教学类-12-11】20240612通义万相-动物图片连连看(A4一页3套)https://blog.csdn.net/reasonsummer/article/details/139599675 用以上的方式,制作图案随机出现的样式
通义千问2(Qwen2)大语言模型在PAI-QuickStart的微调、评测与部署实践
Qwen2(通义千问2)是阿里云最近推出的开源大型语言模型系列,相比2月推出的Qwen1.5,Qwen2实现了整体性能的代际飞跃,大幅提升了代码、数学、推理、指令遵循、多语言理解等能力。其中,Qwen2系列包含5个尺寸的预训练和指令微调模型,Qwen2-0.5B、Qwen2-1.5B、Qwen2-7B、Qwen2-57B-A14B和Qwen2-72B,其中,Qwen2-57B-A14B为混合专家模