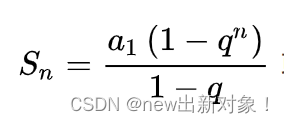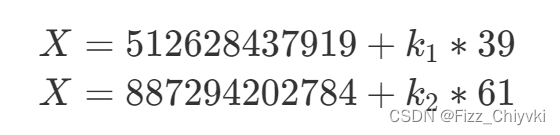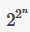费马专题
数论 --- 费马小定理 + 快速幂 HDU 4704 Sum
Sum Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=4704 Mean: 给定一个大整数N,求1到N中每个数的因式分解个数的总和。 analyse: N可达10^100000,只能用数学方法来做。 首先想到的是找规律。通过枚举小数据来找规律,发现其实answer=pow(2,n-1);
同余式,乘法逆元,费马小定理
同余式 同余式是 数论 的基本概念之一,设m是给定的一个正整数,a、b是整数,若满足m| (a-b),则称a与b对模m 同余 ,记为a≡b (mod m),或记为a≡b (m)。 这个式子称为模m的同余式,若m∤ (a-b),则称a、b对模m不同余 同余概念又常表达为: 1.a=b+km (k∈Z); 2.a和b被m除时有相同的 余数 乘法逆元 乘法逆元的定义:在数学领域,对于群G
多校第一场 费马小定理+模拟+组合数学
A题:Couple doubi 链接:http://acm.hdu.edu.cn/showproblem.php?pid=4861 这题逗逼了,刚开始根本就没什么思路,刚开始看题的时候有点像费马小定理,但是这个定理我只知道,然后没用过。看了下定义,有点不一样的是反着的,然后反着的我又不会转化,尼玛,就这样错过了最好的解题方法。然后队友又理解错题意了。WA了多发,然后我重新看了下题意,然后队友才
HDU - 4704 Sum (费马小定理 + 快速幂)
Description Sample Input 2 Sample Output 2 Hint 1. For N = 2, S(1) = S(2) = 1. 2. The input file consists of multiple test cases. 题意:求1-n中,组成n的不同种数 思路:首先我们要先
Project Euler_Problem 160_Factorial Trailing Digits_费马小定理,威尔逊定理,左右互搏
原题目: 题目大意:1e12的阶乘,不算末尾的0,后5位数字为多少 解题思路: 暴力运算也能算,就是有点慢,优化过后可能也得算个几十分钟 这里考虑使用威尔逊定理+费马小定理 用这个方法我们就可以得到对于任何一个小于p的数n,p为素数,n!在模p下的结果, 对于本题: 则我们要找的答案应该是512628437919+k*39的最后几位有效数字,当k>100000时,显然末尾数字就
费马小定理(应用+拓展)
费马小定理(应用+拓展) 定义:如果两个整数a,p互质,也就是gcd(a,p)=1,那么a^(p-1)≡1( mod p). 公式拓展一下 拓展公式1:n*a^(p-1)≡n(mod p) 拓展公式2:a^(p-2) ≡ a ^(-1) (mod p) 拓展公式3:a^b ≡ a^(bmod(p-1)) (mod p) 求(A/B)%999983,但由于A很大,我们只给出n(n=A%9999
算法学习系列(二十七):欧拉函数、欧拉定理、费马小定理
目录 引言一、欧拉函数1.概念2.求每个数的欧拉函数 二、线性筛法求欧拉函数三、欧拉定理,费马小定理 引言 本文主要介绍欧拉函数、线性筛法求欧拉函数,以及公式是怎样推导出来的,并且介绍了欧拉定理,以及费马小定理是怎样被推导出来的。 一、欧拉函数 1.概念 欧拉函数 ϕ ( N ) : 欧拉函数\phi(N): 欧拉函数ϕ(N): 1 ~ N中与N互质的数的个数,(互质:公
【数学】完全剩余系与费马小定理
完全剩余系 我们定义 a i ( 1 ≤ i ≤ n ) a_i(1\le i\le n) ai(1≤i≤n) 为模 m m m 的完全剩余系当且仅当对于 1 ≤ i , j ≤ n 1\le i,j\le n 1≤i,j≤n 且 i ≠ j i\ne j i=j,满足 a i ≢ a j ( m o d m ) a_i\not\equiv a_j\pmod m ai≡aj
hdu 4704 Sum(费马小定理)
数论,费马小定理 a^(p-1) % p == 1,长见识了 #include <cstdio>#include <algorithm>#include <vector>using namespace std;typedef __int64 ll;const int MAXN = 100005;char s[MAXN];const ll mod = 1000000007;ll
[BZOJ 1951][Sdoi2010]古代猪文:Lucas定理|中国剩余定理|费马小定理|扩展欧几里得
点击这里查看原题 一道综合了各种数论的神题。其实不难,主要是需要组合在一起运用。 1.费马小定理:求G^P时使用,因为G^(mod-1)%mod=1,所以需要P%=mod-1 2.Lucas定理&中国剩余定理:计算组合数取模时使用,但是本题中mod-1不为素数,因此需要结合中国剩余定理使用(即扩展Lucas定理) 3.扩展欧几里得:中国剩余定理要求逆元 /*User:SmallLan
洛谷 U5122 T2-power of 2(费马小定理)
U5122 T2-power of 2 题目提供者胡昊 题目描述 是一个十分特殊的式子。 例如: n=0时 =2 然而,太大了 所以,我们让对10007 取模 输入输出格式 输入格式: n 输出格式: % 10007 输入输出样例 输入样例#1: 2 输出样例#1: 16 说明 n<=1000000 /*费马小定理.2^p-1%p=1(p为质数)
素数 (性质,费马小定理 miller_rabin_素性测试)
转载自Matrix大牛的博客 把代码翻译成C++ http://www.matrix67.com/blog/archives/234 一个数是素数(也叫质数),当且仅当它的约数只有两个——1和它本身。规定这两个约数不能相同,因此1不是素数。对素数的研究属于数论范畴,你可以看到许多数学家没事就想出一些符合某种性质的素数并称它为某某某素数。整个数论几乎就围绕着整除和素数之类的词转过去转过来。对于写
(HDU6440)2018中国大学生程序设计竞赛 - 网络选拔赛 - 1003 - Dream - (费马小定理)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6440 题意:给出素数p,要求自定义乘法与加法使得对于任意n,m∈[0,p-1],都能满足(m+n)^p=m^p+n^p。自定义加法是指你自己构造出p*p的矩阵,让第i行第j列表示i+j的自定义值。自定义乘法也构造这样一个矩阵。 且有附加条件:存在q(0<q<p)使得集合{q^k | 0<k<p,k
费马小定理,876. 快速幂求逆元
876. 快速幂求逆元 - AcWing题库 给定 n 组 ai,pi,其中 pi 是质数,求 ai 模 pi 的乘法逆元,若逆元不存在则输出 impossible。 注意:请返回在 0∼p−1 之间的逆元。 乘法逆元的定义 若整数 b,m 互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a×x(modm),则称 x 为 b 的模 m 乘法逆元,记为 b
数论之扩展欧几里得,费马小定理,欧拉定理 + 求最小乘法逆元
目录 1 逆元定义2 欧几里得算法(求最大公约数)3 扩展欧几里得算法3.1 预备知识3.2 关于扩展欧几里得算法3.3 模板3.4 算法推导过程3.5 利用拓展欧几里得算法求逆元 4 费马小定理4.1 定义4.2 模板 5 欧拉定理6 RSA公钥密码经典例题6.1 题目描述6.2 分析6.3 题解 前两天二刷了《模仿游戏》,Alan Turing在二战中研制的图灵机破译了德
欧拉函数,欧拉定理,费马小定理介绍及模板
介绍 欧拉函数的定义:对于正整数 n n n,欧拉函数是小于等于nnn的数中,与 n n n互质的数的数目欧拉函数又称ϕϕ\phi函数,例如 ϕ(8)=4 ϕ ( 8 ) = 4 \phi(8)=4,因为1,3,5,7均和8互质 定理: 如果 n n n为某一个素数ppp,则: ϕ(p)=p−1 ϕ ( p ) = p − 1 \phi(p)=p-1如果 n n n为某一个素数p