解方程专题
【noip】解方程 秦九韶算法
解方程 描述 已知多项式方程: a0+a1x1+a2x2……+an−1xn−1+anxn=0 a_0+a_1x^1+a_2x^2……+a_{n-1}x^{n-1}+a_nx^n=0 求这个方程在[1, m]内的整数解(n 和 m 均为正整数)。 输入格式 输入共 n+2 行。 第一行包含 2 个整数 n、m,每两个整数之间用一个空格隔开。 接下来的 n+1 行每行包含一个整数,依次为
HDU 2199 Can you solve this equation? NYOJ 503 解方程
题目链接~~> 做题感悟:这个题太坑(也许暗示着对二分还没掌握好),调精度调了半上午才调出来。 解题思路:在[ 0 , 100 ] 这个区间里函数是单调递增的所以与二分有一点的差别(个人感觉),只要在 F( 0 ) ~ F( 100 ) 之间的值都有解不断二分即可,也不用加 0.000001 ,其实加也可以. 总结一下 pow ( x , y ) :
NJUST 1926 琪露诺的算术教室 (解方程 大数)
琪露诺的算术教室 Time Limit: 1000ms Memory Limit: 65536KB Description 给出一个非负整数A,将这个数字的最低位移动到最高位(原来的最高位变为次高位,次低位变成最低位),得到非负整数B,发现B恰好是A的k倍。现给出A的最低位的值n,和倍数k,求最小的非负整数B。 Input 第一行输入一个正整数T(1 <= T <
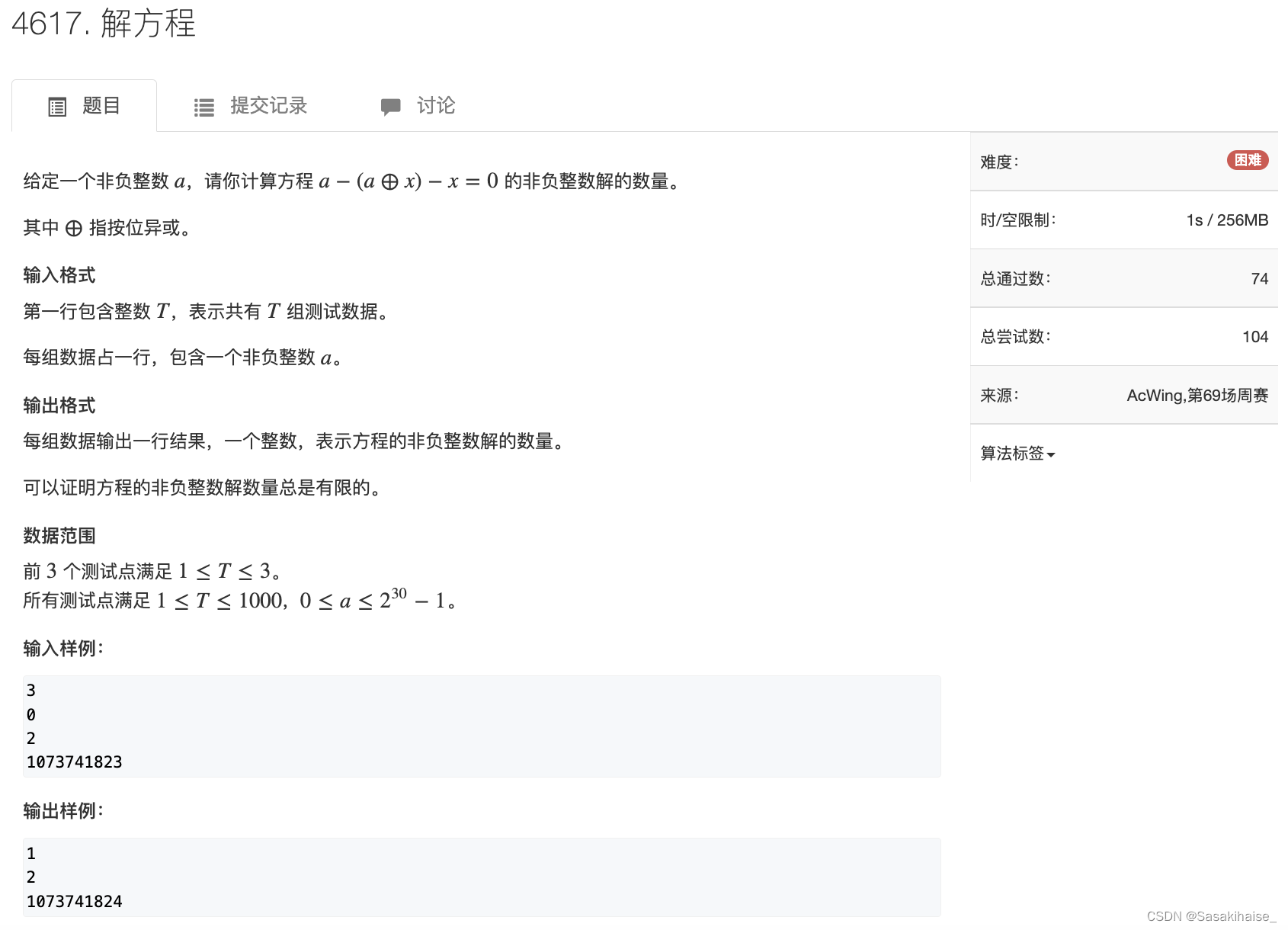
AcWing 4617. 解方程
4617. 解方程 - AcWing题库 【分析】移项之后得到a^x = a-x,把a转为二进制,举个🌰1001 对于为1的位:如果x相应的位置填1,相减之后为0,异或之后为0,相同并且对前面的位没有影响;如果x相应的位置填0,想减之后为1,异或之后也为1,相同并且对前面的位也没影响。 对于为0的位:如果x相应的位置填0,想减之后为0,异或之后也为0,相同并且对前面的位也没影响;但是
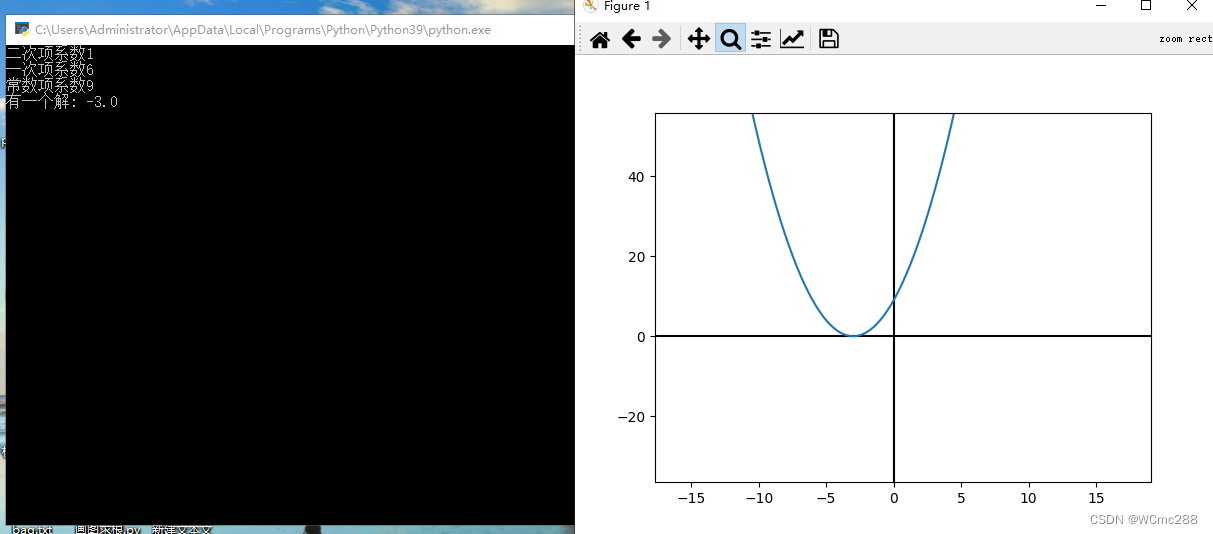
懒人初三党必备---二次函数解方程加画图辅助理解的工具
总所周知,初三学的最烦的就是解方程,要十字相乘法,公式法等,尤其是碰到要画函数草图的题,就又要慢慢算,但是,这个工具可以大概解决这些烦恼 源码如下(所需要库:matplotlib,numpy): import numpy as npimport matplotlib.pyplot as plta=float(input('二次项系数'))b=float(input('一次项系数'))
方便快捷的求导求积分解方程在线工具sage介绍
有时候我们需要进行一些复杂的数学计算,比如求导, 求积分,解方程,还是用abcd字母代表变量的方程等,这就需要进行复杂的数学运算还需要具备良好的数学基础。不过现在有一个非常方便的在线工具,只需要几秒钟, 就能告诉我们所有的答案。 sage &ems;sage是一个免费开源的数学计算软件系统, 里面包含了许多的package,比如NumPy, SciPy, matplotlib, Sympy
线性代数(四)| 解方程 齐次性 非齐次性 扩充问题
文章目录 1 方程解的个数2 解方程步骤2.1 齐次性方程组2.2 非齐次方程组 3 一些扩充问题 系数矩阵 增广矩阵 A m × n X = B A_{m×n}X=B Am×nX=B 1 方程解的个数 m 代表有m个方程 n代表有n个未知数 系数矩阵的秩与增广矩阵的秩不同 无解 若相同 ,如系数矩阵的秩和未知数个数n相同,则有唯一解,若系数矩阵的秩小于未知数个数n
记录一段帮朋友写的代码,使用牛顿-拉夫逊方法解方程
要求 已知公式: t = G + A B F r + B r 2 2 F + A 2 B + G A F ln ( r − A ) + C o n s t t=\frac{G+AB}{F}r+\frac{Br^2}{2F}+\frac{A^2B+GA}{F}\ln (r-A)+Const t=FG+ABr+2FBr2+FA2B+GAln(r−A)+Const 其中 t 的值为0-1
C语言用二分法求解方程解,C语言二分法解方程,急!谢谢!
满意答案 w616041189 2014.06.24 采纳率:46% 等级:11 已帮助:6652人 本题的一个完整的c程序如下,程序在win-tc下调试通过,结果正确。 #include #include #include #include int n; double c[16]; double Func(double); int BisectRoot(double,double,d
Methematica基础教程,适用于初学者,基本入门操作,解方程等
文章目录 一. 笔记本新建及输入输出(计算)二. 基本符号使用三. 容易出错的细节四. 基本函数五. 解方程六. 画图七. 小技巧及小毛病解决 Mathematica初学笔记(比较傻瓜) 自己整理的一些Mathematica的基本用法,包括输入,画图,基本运算及方程组求解,公式导出,以及自己容易犯的错误。我用的是Mathematica 12.0,学习资料为B站视频 一.
python怎么算二元一次方程_python如何解方程的三种方法
python求解方程组的三种方法: 相关推荐:《python视频》 Numpy求解方程组x + 2y = 3 4x + 5y = 6 当然我们可以手动写出解析解,然后写一个函数来求解,这实际上只是用 Python 来单纯做“数值计算”. 但实际上,numpy.linalg.solve 可以直接求解线性方程组. 一般地,我们设解线性方程组形如 Ax=b,其中 A 是系数矩阵,b 是一维
使用MATLAB的solve解方程:单变量,多变量,方程组
单变量 clear,clc;syms x;answ = solve(sin(x)==1,x) 一个等号表示赋值,两个等号才表示相等 % answ =% % pi/2 对于单变量也可省略未知数 answ = solve(sin(x)==1) 也可以这样写 clear,clc;syms x;equ = (sin(x)==1);%equ = sin(x)==1;an
【问题思考总结】解方程的时候什么时候可以消去方程?如何保证不丢解?
问题 在高数中,利用拉格朗日乘数法求解方程的时候,时常不知道化简的时候是否丢解了。 在线代中,面对同解的时候解方程,我又想到将两个方程化成一个方程是否丢解?而且老师根本没有强调过这个问题,似乎是默认了一些方程的存在。 在概率论中,面对条件概率,或者联合概率密度的值的代入的问题,同样引发了我对这个问题的记忆。 这个问题困扰我许久,今天在做线代的时候想出一个在线性代数中理解的方法,因此下面的例子也是