本文主要是介绍【问题思考总结】解方程的时候什么时候可以消去方程?如何保证不丢解?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题
在高数中,利用拉格朗日乘数法求解方程的时候,时常不知道化简的时候是否丢解了。
在线代中,面对同解的时候解方程,我又想到将两个方程化成一个方程是否丢解?而且老师根本没有强调过这个问题,似乎是默认了一些方程的存在。
在概率论中,面对条件概率,或者联合概率密度的值的代入的问题,同样引发了我对这个问题的记忆。
这个问题困扰我许久,今天在做线代的时候想出一个在线性代数中理解的方法,因此下面的例子也是用线代中方程组同解的问题来说明。
思考

可以看到,在上面两个方程中,l对应的是两个方程的公共解,那么是否可以直接变成上述上面式子的单一方程呢?(也是老师直接给出的方程)直观上来讲是很正确的,但是出于严谨和通用性的角度来考虑,我认为他是错误的。
首先,我们什么时候能够消去一个方程? 在高数中找不到答案,因为直观上来说(个人感觉),我直接把这个两个式子加起来似乎没有什么变化,和原来的方程也没有什么区别。
在线代中却可以比较直观的看出,通过刚才的变化,实际上是把矩阵的第二行从左式变到右式,并且去掉了第一个式子。
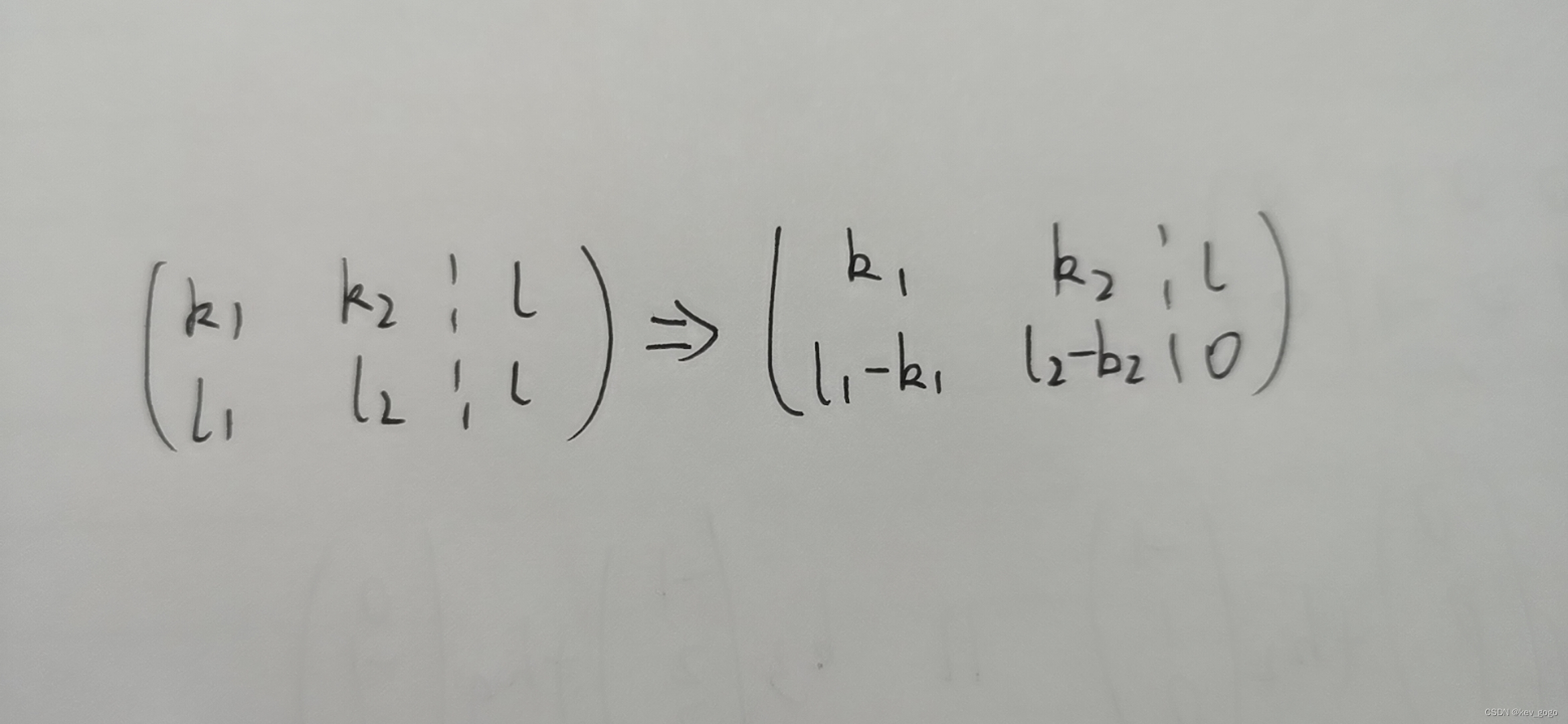
那么问题就变成了我们能否去掉第一个式子并且保证方程组是等价的:

当然是不可以的,否则未知量l就无法被表示了(从线性相关的角度想了想有点绕)。因此,我们不能从方程组中随便去掉一个方程,除非可以化成000,或者可以明确看出是线性相关的情况。
总结
在解方程的时候,不可以轻易的去掉方程,如果想要去掉,需要证明,不能想当然,否则可能会造成丢解的情况。在三门课程(高数,线代,概率论)中都要注意,均有应用。
这篇关于【问题思考总结】解方程的时候什么时候可以消去方程?如何保证不丢解?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





