第五十七专题
代码随想录算法训练营第五十七天 | 图论part07
53. 寻宝 prim算法 prim算法 #include <iostream>#include <vector>#include <fstream>#include <climits>using namespace std;int main() {int v, e;int v1, v2, val;ifstream infile("input.txt");cin >> v >> e;ve
![[leetcode hot150]第五十七题，插入区间](https://img-blog.csdnimg.cn/direct/f5d97d13edab4ac397ffbb5352abc509.png)
[leetcode hot150]第五十七题，插入区间
题目： 给你一个 无重叠的 ，按照区间起始端点排序的区间列表 intervals，其中 intervals[i] = [starti, endi] 表示第 i 个区间的开始和结束，并且 intervals 按照 starti 升序排列。同样给定一个区间 newInterval = [start, end] 表示另一个区间的开始和结束。 在 intervals 中插入区间 newInterval
代码随想录算法训练营第五十七天｜647 回文子串 516.最长回文子序列
647. 回文子串 https://leetcode.com/problems/palindromic-substrings/ 思路： 当我们看到两个下标 i， j 上 s[i] != s[j], 那么 s[i: j+1] 一定不是回文子串。 如果s[i] == s[j], 那么我们可以在检查 s[i+1: j] 是不是回文串。如果暴力搜索的话是 O(n^3) 的时间复杂度。 我们可以用一个二
随想录算法训练营第五十七天|647.回文子串、516.最长回文子序列
647.回文子串 public class Solution {public int CountSubstrings(string s) {char[] s1=s.ToCharArray();int ans=0;bool[,]dp=new bool[s1.Length,s1.Length];for(int i=s1.Length-1;i>=0;i--){for(int j=i;j<s1.Leng
代码随想录算法训练营第五十七天 647. 回文子串、516.最长回文子序列、动态规划章节总结
代码随想录算法训练营第五十七天 | 647. 回文子串、516.最长回文子序列、动态规划章节总结 647. 回文子串 题目链接：647. 回文子串 - 力扣（LeetCode） // dp法class Solution {public int countSubstrings(String s) {int len = s.length();int count = 0;/**当s[i] !=
代码随想录算法训练营第五十七天| 647. 回文子串、516.最长回文子序列、动态规划总结篇
文章目录 1.回文子串2.最长回文子序列3.动态规划总结篇 1.回文子串 给你一个字符串 s，请你统计并返回这个字符串中回文子串的数目。 回文字符串是正着读和倒过来读一样的字符串。 子字符串是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。 示例 1： 输入：s = “abc” 输出：3 解释：三
代码随想录算法训练营第五十七天 | 647. 回文子串、516. 最长回文子序列
647. 回文子串 题目链接：647. 回文子串 给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。 文章讲解/视频讲解：https://programmercarl.com/0647.%E
代码随想录训练营第五十七天| ● 647. 回文子串 ● 516.最长回文子序列● 动态规划总结篇
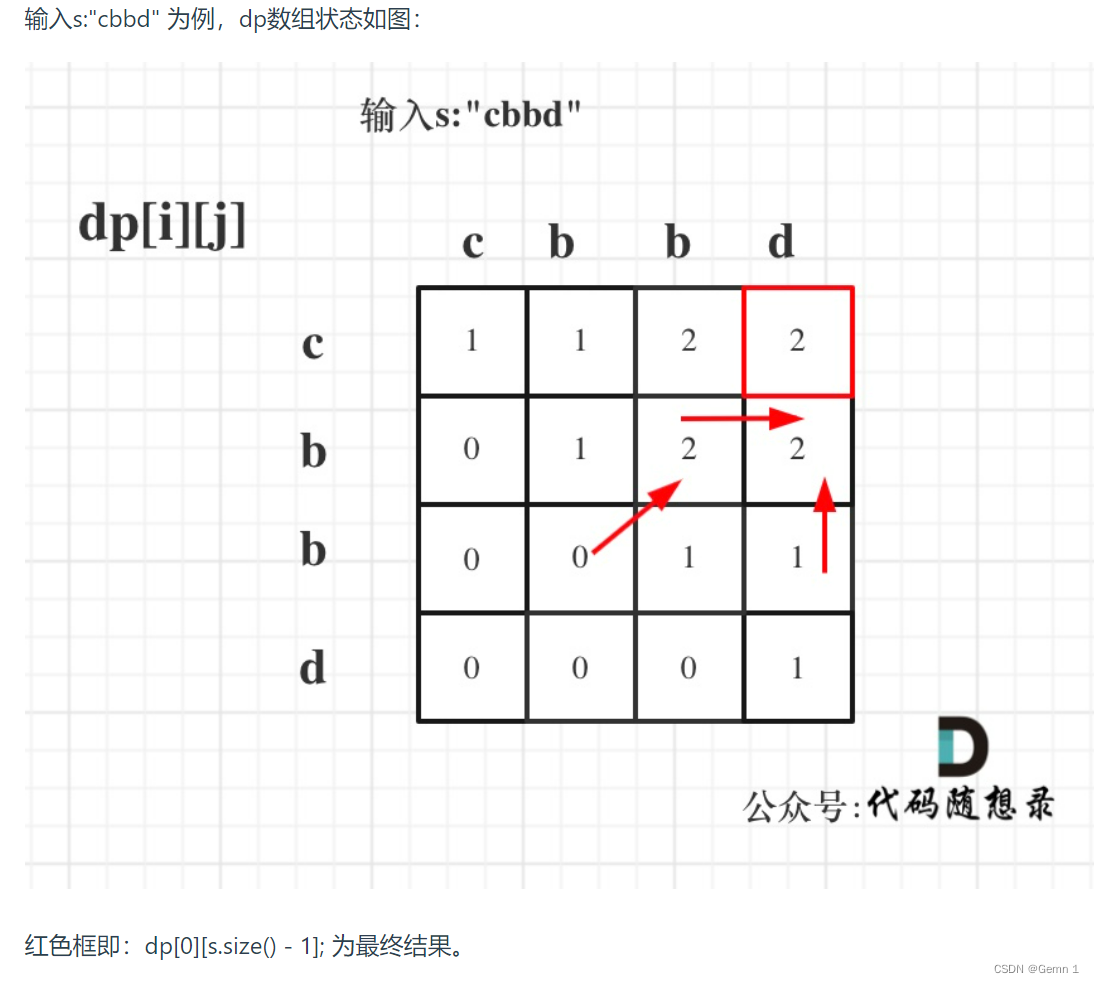
647. 回文子串 动态规划解决的经典题目，如果没接触过的话，别硬想 直接看题解。 代码随想录 dp数组定义：布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是，dp[i][j]为true，否则为false。 递推公式：[i,j]的子串有两种情况：若s[i]==s[j]，如果[i+1,j-1]的子串是回文串，那么[i,j]的子串也为
算法训练第五十七天|647. 回文子串、516.最长回文子序列
647. 回文子串： 题目链接 给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。 示例 : 输入：s = "abc"输出：3解释：三个回文子串: "a", "b", "c" 解答：
C语言第五十七弹---模拟使用memmove函数
使用C语言模拟使用memmove函数 memmove是一个C语言库函数，用于在内存中移动一块数据。它可以在源地址和目标地址之间复制任意大小的数据块，并且会处理重叠的情况。即使源和目标是重叠的，memmove函数也可以确保数据被正确复制。 源定义 void* memmove(void* dest, const void* src, size_t n); dest是指向目标位置的指针，src
代码随想录算法训练营第五十七天|647.回文子串\516.最长回文子序列
确定dp数组（dp table）以及下标的含义 确定递推公式 dp数组如何初始化 确定遍历顺序 举例推导dp数组 647.回文子串 确定dp数组（dp table）以及下标的含义 dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。 确定递推公式 整体上是两种，就是s[i]与s[j]相等，s[i
代码随想录算法训练营 ---第五十七天
今天是两道动态规划的经典题目。 第一题： 简介： 做了今天的题目我有了新的理解，我觉得过去我过于注重对于二维数组的理解，忽略了对dp数组i 和 j 的含义的理解。 动态规划五部曲： 1.确定dp数组的含义 本题我们将i 和 j 看作是 s字符串两端，所以我们将其定义为 i和j 之间的子串是否为回文子串。 有人会问为何我们不像往常一样，将dp含义定义为问题所问，是因为我
代码随想录第五十七天|● 392.判断子序列 ● 115.不同的子序列
392.判断子序列 题目： 给定字符串 s 和 t ，判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。 进阶： 如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下
代码随想录算法训练营第五十七天| LeetCode 392 判断子序列、LeetCode 115 不同的子序列
1 LeetCode 392 判断子序列 题目链接：LeetCode 392 判断子序列 文章讲解：代码随想录(programmercarl.com) 视频讲解：动态规划，用相似思路解决复杂问题 | LeetCode：392.判断子序列 2 LeetCode 115 不同的子序列 题目链接：LeetCode 115 不同的子序列 文章讲解：代码随想录(programmercarl
代码随想录算法训练营第五十七天| LeetCode 392 判断子序列、LeetCode 115 不同的子序列
1 LeetCode 392 判断子序列 题目链接：LeetCode 392 判断子序列 文章讲解：代码随想录(programmercarl.com) 视频讲解：动态规划，用相似思路解决复杂问题 | LeetCode：392.判断子序列 2 LeetCode 115 不同的子序列 题目链接：LeetCode 115 不同的子序列 文章讲解：代码随想录(programmercarl
代码随想录算法训练营第五十七天 |392.判断子序列、115.不同的子序列
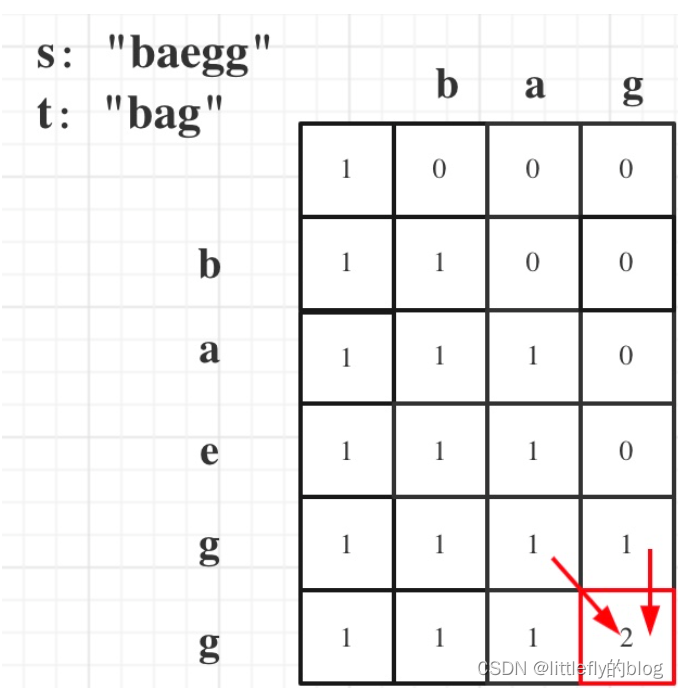
一、392.判断子序列 题目链接/文章讲解/视频讲解：代码随想录 思考：本题和 1143.最长公共子序列有很大的相似之处 1.确定dp数组（dp table）以及下标的含义 dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j] 2.确定递推公式 if (s[i - 1] == t[j - 1]) dp[i][j]
第五十七集 MySQL 索引 方便管理
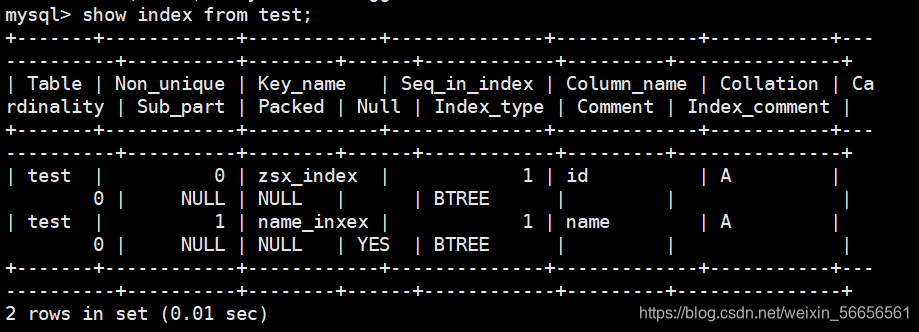
MySQL 索引知识点 方便管理 索引的应用索引的作用索引的副作用： 索引的分类普通索引修改表方式创建索引创建表的时候指定索引唯一性索引创建表时指定唯一索引修改表方式创建主键索引组合索引全文索引查看索引各字段的含义如下：删除索引总结 ## 索引的概念 ●索引是一个排序的列表，在这个列表中存储着索引的值和包含这个值的数据所在行的物理地址（类似于C语言的链表通过指针指向数据记录的
代码随想录算法训练营20期|第五十七天|动态规划part15|● 392.判断子序列 ● 115.不同的子序列
392.判断子序列 class Solution {public boolean isSubsequence(String s, String t) {int len1 = s.length();int len2 = t.length();int[][] dp = new int[len1 + 1][len2 + 1];for(int i = 1; i <= len1; i++) {f
代码随想录算法训练营20期|第五十七天|动态规划part15|● 392.判断子序列 ● 115.不同的子序列
392.判断子序列 class Solution {public boolean isSubsequence(String s, String t) {int len1 = s.length();int len2 = t.length();int[][] dp = new int[len1 + 1][len2 + 1];for(int i = 1; i <= len1; i++) {f