本文主要是介绍代码随想录算法训练营 ---第五十七天,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
今天是两道动态规划的经典题目。
第一题:

简介:
做了今天的题目我有了新的理解,我觉得过去我过于注重对于二维数组的理解,忽略了对dp数组i 和 j 的含义的理解。
动态规划五部曲:
1.确定dp数组的含义
本题我们将i 和 j 看作是 s字符串两端,所以我们将其定义为 i和j 之间的子串是否为回文子串。
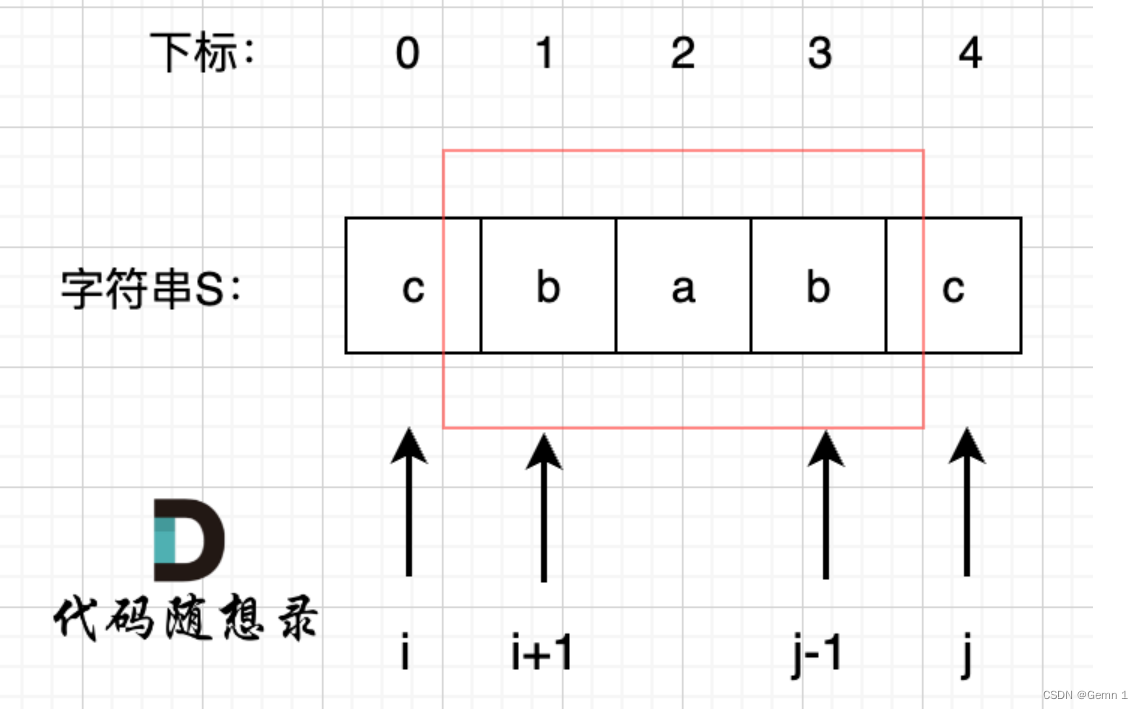
有人会问为何我们不像往常一样,将dp含义定义为问题所问,是因为我们定义dp数组是为了找出其中的递推关系。帮助我们更好的解题。那么此时我们是不是能找到一种递归关系,也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文。所以为了明确这种递归关系,我们的dp数组是要定义成一位二维dp数组。布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
2.确定dp数组的递推公式
两种情况 s[i] == s[j]
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
s[i] != s[j] dp[i][j] = false
3.确定数组的初始化
都初始化为false
4.确定遍历顺序
怎么遍历要看我们的递推公式我们呢可以看出是从左下往右上推导 所以我们从上到下,从左到右遍历
5.打印数组
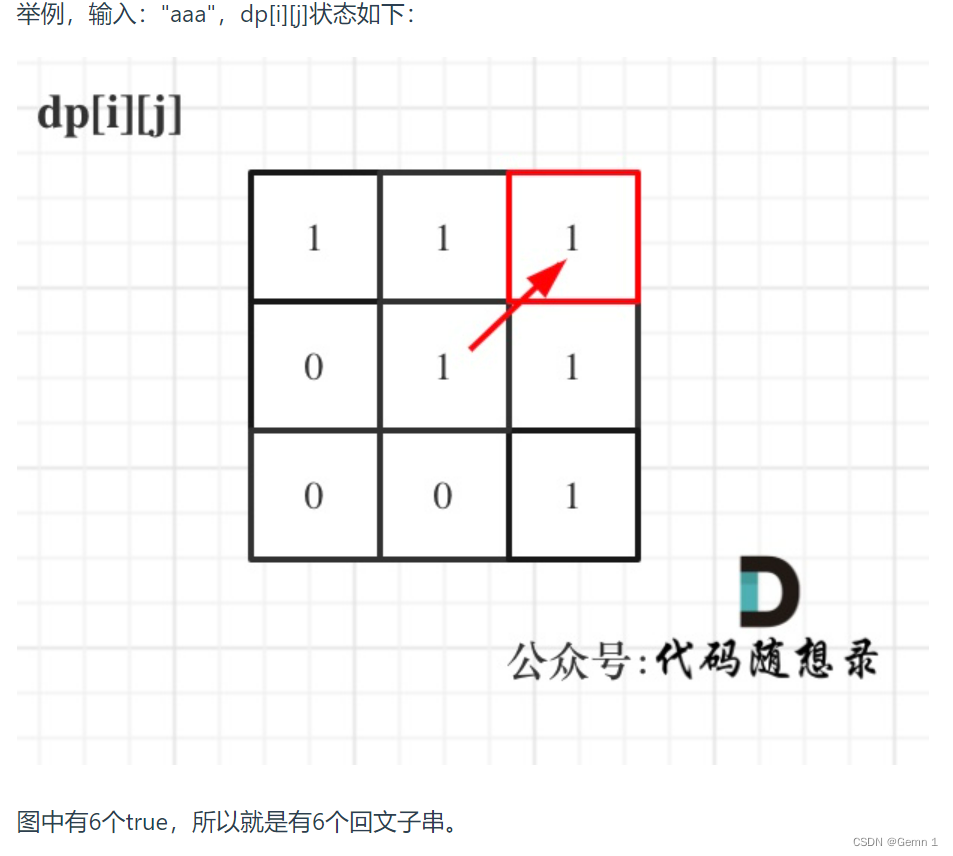
代码实现:
int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) { // 情况一 和 情况二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情况三result++;dp[i][j] = true;}}}}return result;}第二题:

简介:
本题相较于上题有所不同,首先上题是连续的子串,本题可以是不连续的。但是思路相差不大,都是将dp模型i 和 j 看作是 s字符串两端,但是我们将其定义为 i和j 之间的子串的长度。
动态规划五部曲:
1.确定dp数组的含义
将dp模型i 和 j 看作是 s字符串两端,但是我们将其定义为 i和j 之间的子串的长度
2.确定dp数组的递推公式
两种情况: s[i]== s[j] 相等的话我们看 i+1 和 j-1 之间的子串的长度加2 就是当前的长度
dp[i][j] = dp[i+1][j-1]+2
s[i]!= s[j] 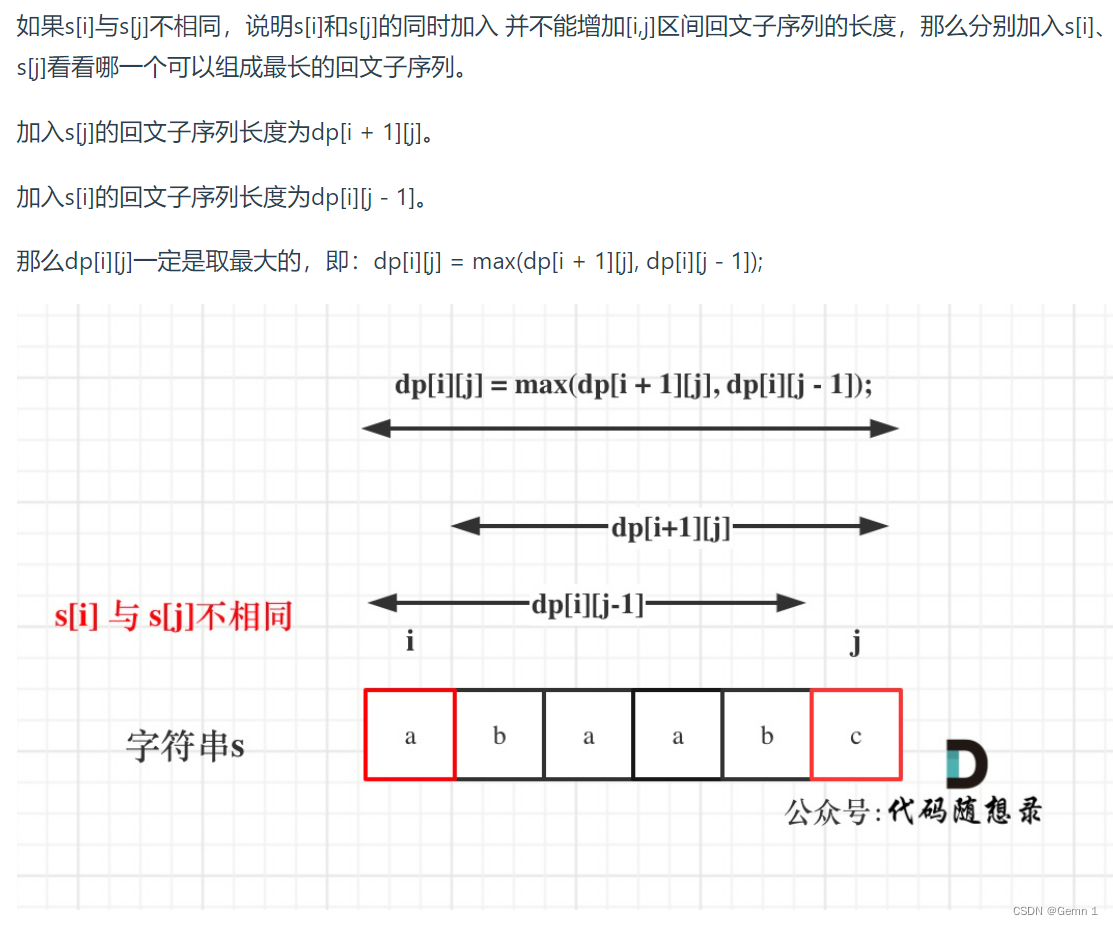
3.确定数组的初始化
因为递推公式原因 我们可以看出 我们无法推到 i 和 j 相同的情况 所以我们将 i 和 j相同的情况初始化为1 因为 一个字符 子串长度为1.
其他初始化为零
4.确定遍历顺序
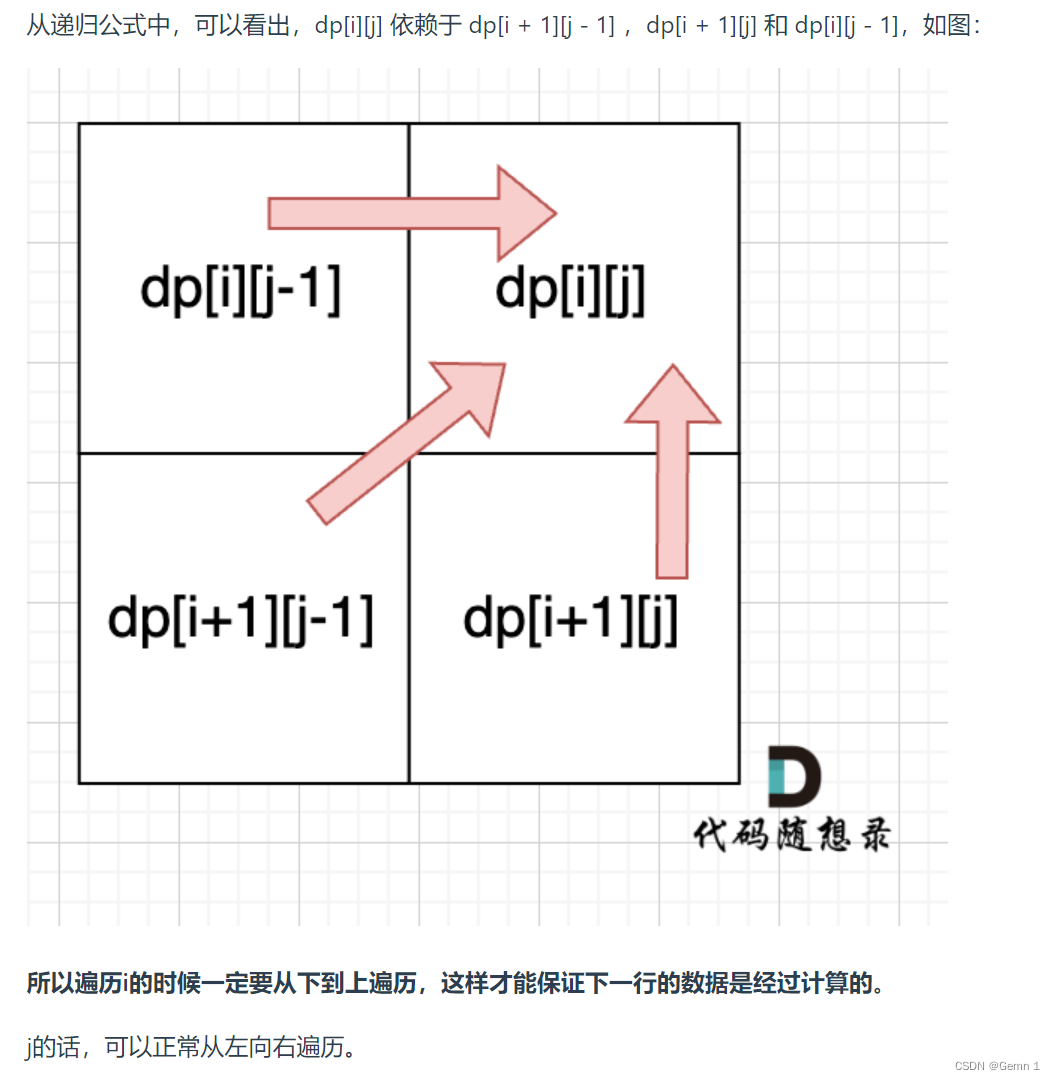
5.打印数组
代码实现:
int longestPalindromeSubseq(string s) {vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));for(int i=0;i<s.size();i++)dp[i][i] = 1;for(int i=s.size()-1;i>=0;i--){for(int j=i+1;j<s.size();j++){if(s[i] == s[j]){dp[i][j] = dp[i+1][j-1]+2;}else{dp[i][j] = max(dp[i+1][j],dp[i][j-1]);}}}return dp[0][s.size()-1];}总结:
动态规划有点折磨,有点抽象。一定要多刷几遍,多理解。继续加油!
这篇关于代码随想录算法训练营 ---第五十七天的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



