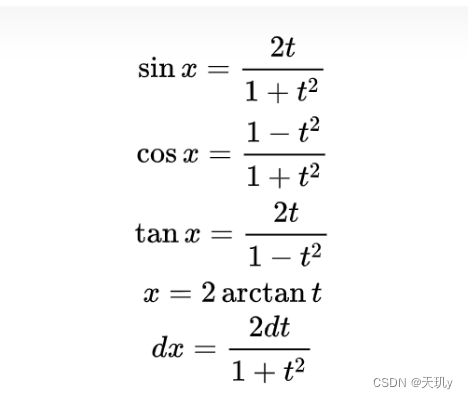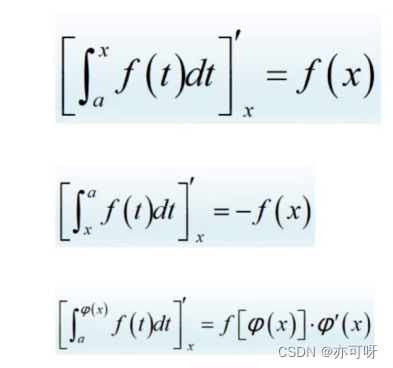积分学专题
考研高数(对比一元微分学和一元积分学概念)
1.一元微分学的概念和一元积分学的概念 一元微分 1.导数 函数一点可导的充要条件:左右导数均存在且相等(也可说左右极限存在且相等) 函数一点可导的必要条件:若f(x)在一点可导,则f(x)在该点连续。反之未必。 2.导数的几何意义 函数y=f(x) 在x=x0处的导数 f′(x0),表示曲线y=f(x)在点P(x0,f(x0))处的切线的斜率k。 注意:一点的导数存在-->
一元函数积分学——刷题(16
目录 1.题目:2.解题思路和步骤:3.总结:小结: 1.题目: 比较这两种题的求解方法 2.解题思路和步骤: 3.13: 这个题就很适合用万能公式,因为可以把1+t2消掉: 也可以用三角恒等式: 3.14: 虽然万能公式总是可以求出三角函数的积分,但是不一定是最好的方法,比如这类题可以使用其他方法: 3.总结: 万能公式: 小结: 关注我给大
2020张宇1000题【好题收集】【第三章:一元函数积分学】
文章目录 三.一元函数积分学性质概念3.2(结论)【导函数与原函数的周期性】 3.43.7 一元积分比大小3.103.13 定积分定义计算3.173.22 换元法一元函数积分复杂与特色计算3.873.883.893.903.923.933.943.95 反常积分判敛与计算3.1033.1043.1053.1253.1303.133(积分曲线)3.136(绕直线旋转) 一元积分的物理应用3.1
【考研数学】高等数学第三模块——积分学 | Part III 二重积分
文章目录 引言一、概念与基本性质1.1 实际应用背景(1)平面薄片的质量(2)曲顶柱体的体积 1.2 二重积分的概念1.3 二重积分的性质 二、积分法2.1 直角坐标法2.2 极坐标法 三、二重积分的应用3.1 几何应用3.2 物理应用 引言 积分学前面两个部分是一元积分的相关内容,今天开始进入重积分的学习。其实如果能理解好一元积分的定义和特点,稍加练习后,直接接上重积分是
《微积分:一元函数积分学》——不定积分与定积分的存在定理
1、原函数(不定积分)存在定理 (1)连续函数 f(x) 必有原函数 F(x) (2)含有第一类间断点、无穷间断点的函数 f(x) 在包含该间断点的区间内必没有原函数 F(x) 2、定积分存在定理 (1)f (x) 在 [a,b] 上连续,则 存在 (2)若 f (x) 在 [a,b] 上有界,且只有有限个间断点则 存在 另一个充要条件:若 f (x)在 [a,b] 上
高等数学---第十二章多元积分学及其应用---曲面积分
1对弧长的线积分 2对坐标的线积分 3将x的二次方+y的二次方转变为极坐标的方式利用公式求解或者转化为cost与sint的方式求解 4函数为1的线积分结果为周长 5x属于a到b的线积分 6第二类线积分的计算,如果不是密封区域,那就无法直接用格林公式 7补线用格林公式如何处理补上来的线 8直接法对P是求x对t的导数,格林公式对p是求P对y的偏导 9曲
《微积分:一元函数积分学》——不定积分与定积分的存在定理
1、原函数(不定积分)存在定理 (1)连续函数 f(x) 必有原函数 F(x) (2)含有第一类间断点、无穷间断点的函数 f(x) 在包含该间断点的区间内必没有原函数 F(x) 2、定积分存在定理 (1)f (x) 在 [a,b] 上连续,则 存在 (2)若 f (x) 在 [a,b] 上有界,且只有有限个间断点则 存在 另一个充要条件:若 f (x)在 [a,b] 上
一元函数积分学的应用
目录:点我 思维导图下载:点我 一、研究对象 函数 f ( x ) . f(x). f(x).函数列 f n ( x ) . f_n(x). fn(x).用参数方程所给出的函数;偏导函数 ∂ f ∂ x . \frac{\partial f}{\partial x}. ∂x∂f.变限积分函数 ∫ a x f ( t ) d t . \int_{a}^{x}f(t)dt. ∫a
高数 | 【一元函数积分学】定积分、变限积分 一元函数积分学李林880 巧解例题
一、定积分的概念、性质及几何意义 巧解:利用奇偶性,快速选出答案。 利用图形帮助解题。 设出具体函数。 二、定积分的计算 1.利用几何意义 2.换元法巧解 3.区间平移 本题也可用用区间再现 4.绝对值
高数:第三章:一元函数积分学
文章目录 一、不定积分(一)两个基本概念:原函数、不定积分(二)原函数的存在性:原函数存在定理(三)不定积分的性质(四)基本积分公式(五)三种主要积分法1.凑微分 (第一类换元法)2.换元法 (第二类换元法)①三角代换②根式代换③倒代换 3.分部积分法4.其他技巧:积分公式、分项积分法(拆两项)、 -1 +1 、上下同乘 (六)三类常见可积函数积分1.有理函数积分: ∫ R ( x ) d