离散数学专题
离散数学------关系理论
一、序偶和笛卡尔积 序偶 两个序偶如果相等,那么他们相对应的第一第二元素分别相等 笛卡尔积 笛卡尔积是集合之间的一种运算,运算的结果是个序偶,第一元素来自前面的集合,第二元素来自后面的集合。 两集合进行笛卡尔积运算后集合里的元素个数=两集合元素个数的乘积 二、关系 定义 每种关系都可以用序偶表示,关系是两集合笛卡尔积的子集。 表示方式 题型一:求两
离散数学中的逻辑应用(2)
目录 引言 1. 逻辑在决策分析中的应用 2. 逻辑在算法设计中的应用 3. 逻辑在数学证明中的应用 4. 逻辑在编程中的应用 5. 逻辑应用工具 6. 总结 引言 在上一篇文章中,我们介绍了逻辑的基本概念和运算。本篇文章将深入探讨如何将逻辑应用于实际问题中,如问题求解、决策分析和数学证明。通过具体的例子和推理步骤,你将能够理解逻辑在离散数学及其他领域中的广泛应用。
离散数学中的逻辑基础(1)
目录 引言 1. 命题及其逻辑运算 2. 逻辑等价与范式 3. 逻辑推理规则 4. 逻辑问题练习 5. 总结 引言 逻辑是离散数学的核心概念之一,它用于精确描述数学命题并分析其关系。逻辑不仅是数学证明的基础,也是计算机科学中算法设计和编程的基石。本篇文章将详细介绍逻辑学中的命题、逻辑运算和推理规则,帮助读者建立扎实的逻辑基础。 1. 命题及其逻辑运算 1.1 命题的定义
离散数学-代数系统证明题归类
什么是独异点? 运算° 在B上封闭,运算° 可结合,且存在幺元。 学会合理套用题目公式+结合律 零元? 群中不可能有零元 几个结论要熟记: 1.当群的阶为1时,它的唯一元素视作幺元e 2.若群的阶大于1时,且同时存在幺元和零元的话,幺元不等于零元 纯个人理解: 因为零元和什么相乘,依旧是零元。 而零元又不等于幺元。 我们知道,一个
破解凯撒密码(离散数学)
首先来看以下恺撒密码。 离散数学的一道作业题。 凯撒密码作为一种最为古老的对称加密体制,在古罗马的时候都已经很流行,他的基本思想是:通过把字母移动一定的位数来实现加密和解密。例如,如果密匙是把明文字母的位数向后移动三位,那么明文字母B就变成了密文的E,依次类推,X将变成A,Y变成B,Z变成C,由此可见,位数就是凯撒密码加密和解密的密钥。 题目如下: It is known t
C++实现离散数学中求合式表达式
在输入任何一个合式公式后,该段程序就会自动检测里面的命题变元,并要求为之输入真假值, 在输入完毕后就会得出该合式公式的真假值,运用的是递归的思想。 ----------YYC #include<iostream> #include<string> #include<map> using namespace std; /* *说明: * 用!表示 否定
C++实现离散数学“五个房子,不同颜色,不同国家...”问题
有五座房子,每座房子的颜色不同,里面分别住着不同国家的人,每个人都有自己养的不同宠物、喜欢喝的不同饮料、抽的不同牌子的烟。现已知以下一些信息: 1>英国人住在红色的房子里; 2>西班牙人养了一条狗; 3>挪威人住在左边的第一个房子里; 4>黄房子里的人喜欢抽kools牌的香烟; 5>抽chesterfields牌香烟的人与养狐狸的人是邻居;
C#实现离散数学中Kn图一笔画模拟
用C#实现离散数学中的Kn图模拟,该实验中用自己设计的算法实现了一笔画成n各结点的无向完全图动画模拟。 由于本实验没有做异常处理,所以n值只能输入奇数,且必须先点击画点,后才能开始画图。 --------------YYC 节点类 using System.Text; using System.Threading.Tasks; using System.Drawing; name
【离散数学】数理逻辑集合论知识点汇总
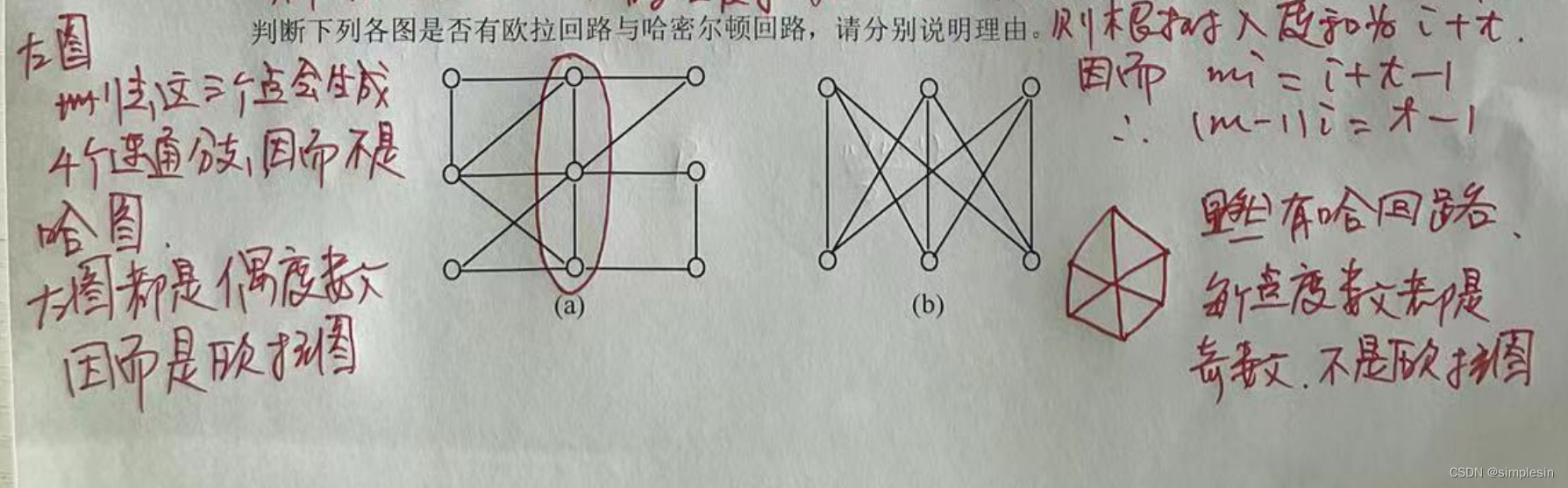
期末题型: 一、 单选题(每题2分,10题共20分) 命题判定、哈斯图边计算等 二、 填空题(每空1分,共20分) 与非和或非的表示等 三、 简答题(10题,每题6分,共60分) 推理的构造证明、等值演算求主范式、前束范式的提取、一阶逻辑的命题定义(类似苏格拉底三段论)、证明给定集合和关系是偏序关系/等价关系等 考试时间:1hour50min
2018年长沙理工大学第十三届程序设计竞赛 K. zzq的离散数学教室2(dilworth定理+有向图可相交路径覆盖 dinic版)
题目 在这个题目中,集合中有n个元素,编号从1到n。它们之间共有m对偏序关系,每一对偏序关系的表示形式为以空格分开的两个编号:x y。含义是x和y之间有关系≤。(这里的≤不是传统意义上的小于等于,可以理解为从y到x的一条有向边),记做:x≤y。同时这些关系也具有传递性,例如,如果x≤y并且y≤z,那么可以得到x≤z。数据保证不会出现同时有x≤y,y≤z,z≤x的情况。 现在我们的问题是,要你从
题库管理系统-基于Springboot实现JAVA+SQL离散数学题库管理系统(完整源码+LW+翻译)
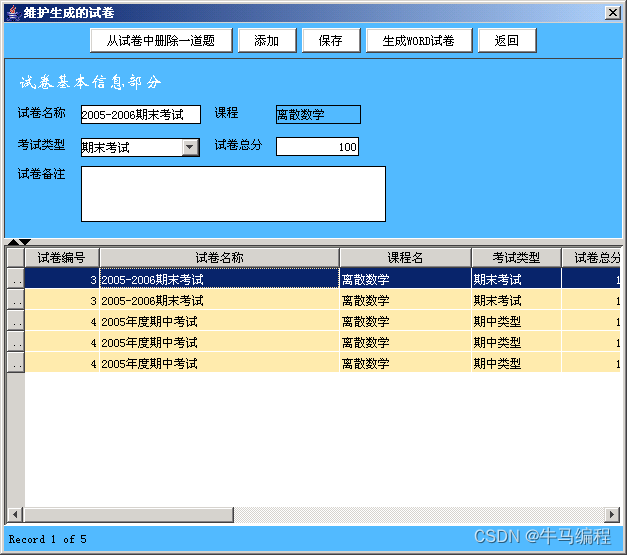
基于Springboot实现JAVA+SQL离散数学题库管理系统(完整源码+LW+翻译) 概述: 本系统具体完成的功能如下: 1题库的管理与维护:新题的录入,修改,删除等功能。 2生成试卷:包括自动生成与手工改动,要求可以对生成的试卷进行打印和WORD排版,并且对生成的试卷能自动生成其参考答案。 其次还应考虑到试题的实际应用性,如:题目的覆盖率,雷同度,难度系数及近三年内不能重题等问题。
离散数学【详解】-自学考试湖北,争取做到识字都能看懂。
回顾8年前,我记得我大学高数没复习,考了23分。 今天公司代码写完了,明天清明节,写篇文章磨磨时间。 我的文章,没有一篇不是磨时间能好好写出来的。 ----我 先列标题,比如h1,h2,这些内容。然后往里面填字,然后读一下改改,有例子的补充一下备注,大概我想写这篇文章的想法就这 逻辑 命题 命题,一个最简单的判断 什么是命题?能够【判断真假】的【陈述句】。看起来很简单对吧
离散数学命题逻辑连接词的解释
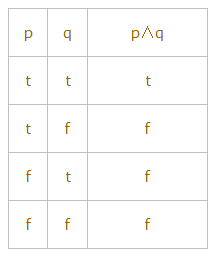
命题逻辑连接词 在自然语言中,常常使用“或”,“与”,“但是”等一些联结词,对于这种联结词的使用,一般没有很严格的定义,因此有时显得不很确切。在数理逻辑中,复合命题是由原子命题与逻辑联结词组合而成,联结词是复合命题中的重要组成部分,为了便于书写和进行推演,必须对联结词作出明确规定并符号化。下面介绍各个联结词。 (1)否定 定义1-2.1设p为一命题,p的否定是一个新的命题,记作┓p.若p为t, ┓
南邮离散数学实验1 (简单版) 根据真值求真值表和主范式
#include <iostream>#include <cmath>using namespace std;int const MAX = 1e6;short true_value[MAX]; //真值short true_table[MAX][10]; //真值表short pdnf[MAX]; //主析取范式short pcnf[MAX]; //主合取范式char
南邮离散数学实验2 集合上二元关系性质判定的实现
#include <iostream>using namespace std;int const MAX = 1000; int matrix[MAX][MAX]; //矩阵int n; //集合元素个数bool flag1, flag2, flag3, flag4, flag5;void Reflexive() //自反{flag1 = tru
《离散数学导学》精炼——第8章(关系)
学无止境追求真,勤奋刻苦起点新。每日精进千里路,成功不是梦想闲。 文章目录 引言正文第八章 关系定义定义域,值域关系的逆关系上的运算(重点)关系的合成同类关系和异类关系关系的性质(重难点)顺序与等价(简介)闭包多元关系 引言 笔者一直觉得在计算机这一学科的学习中,离散数学是极为重要的知识基础。离散化的思想体现在计算机学科的方方面面。举例来说,“像素”这一概念是我们日常
离散数学:关系的性质
一、前言 本文将简单介绍二元关系的性质:(1)自反性(2)对称性(3)传递性,以及由此派生出的其他性质。 二、二元关系的性质 2.1 自反性定义 (1)若, 则称R在A上是自反的。 (2)若,则称R在A上是反自反的。 2.2 对称性定义 设R为A上的二元关系, (1)若,则称R为A上的对称关系 (2) 若,则称R为A上的反对称关系 2.3 传递性定义