汉诺塔专题
HDU 2064 汉诺塔III(水题)
题目: http://acm.hdu.edu.cn/showproblem.php?pid=2064 题目大意: 有三根杆,求把n个圆盘从左边移到右边,最少需要移动圆盘的次数。移动规则为大盘不能放在小盘上,比原始的汉诺塔题改变的地方是,只能通过中间的杆往左右两边的杆移动。 心得: 此题心得在题外,不在题内,初看此题,尼玛吓了一跳,好像很难的样子,手贱百度了一下,只注意到俩字“水题”,赶紧
【递推】【DP】-HDU-2064-汉诺塔③
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2064 题目描述:从最左边移到最右边柱子的过程中必须经过中间柱子。 解题思路: 进ACM组时候的考试题,当时虐我的题终于被我虐回来了。。一眼看出方程,1A了。。。呵呵。。满足一下我的虚荣心,,,抚慰一下受挫的心灵吧。 AC代码: #include <iostream>using names
【递推】【DP】-HDU-1996-汉诺塔⑥
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1996 题目描述:问三个柱子上放N个盘子,一共可能有多少种组合?(可以有柱子不放,放的时候依然满足下面盘子比上面盘子大) 解题思路: 对于放N个盘子,ans [ N ] = 3 + 6 * f ( N ) +6 * g ( N ) 这三项依次代表这N个盘子分成一堆,两堆,三堆时有多少种可能。排列
【递推】【DP】-HDU-1995-汉诺塔⑤
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1995 题目描述:计算汉诺塔中某个盘子的移动次数 解题思路: 想了好久,突然顿悟! 思路如下,所谓递推,即是前者与后者存在直接联系,由前者可以直接推出后者,因此必须有一端是已知的,这题里显然最下面的盘子只被动了一次,这就是开端,然后我们考虑紧挨着的两张盘子的递推关系,发现上面盘子是紧挨着的下面盘
【递推】【DP】-HDU-1207-汉诺塔②
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1207 题目描述:四柱汉诺塔 解题思路: 开始想了方程 f [ n ] = 2 * f [n - 2] + 3和 f [ n ] = 2 * f [n - 3] + 7。结果都不对,很郁闷,纠结半天之后,上网查攻略去了,啊!我就差一点了,但也是差了最为关键的一步! 正确的方程应该是: f [
Python 汉诺塔递归原理
# -*- coding: utf-8 -*- # 递归的重点在于放弃,放弃理解和跟踪递归全程的企图,只理解递归两层之间的交接,以及递归的终结条件def move(n, start, mid, end): # n:盘子,start起始区,mid中转区,end终点区if n == 1:print('move', start, '-->', end)else:move(n-1, start, e
迭代和递归(Python)--乘方、最大公约数、汉诺塔、斐波那契、回文字符串
1.迭代 def iterPower(base,exp):result=1.0while exp>0:result*=baseexp-=1return result 运行结果: 2.递归的乘法运算: def recurMul(a,b):if b==1:return aelse:return a+recurMul(a,b-1) 运行结果: 3.递归乘方
青蛙跳台阶与汉诺塔问题
hello,各位小伙伴们上次我们复习了C语言小tip之函数递归,这次我们来使用函数递归来完成青蛙跳台阶和汉诺塔问题! 青蛙跳台阶问题 青蛙跳台阶问题:一只青蛙跳n阶台阶,一次可以跳1阶或者两阶,问有多少种情况! 如果跳1节台阶的话,只有一种情况,如果跳2节台阶的话,有两种情况一次跳一阶,或者一次性跳两阶。如果跳3节台阶的话,可以选择一次跳一节,或者第一次跳一节,第二次跳两节或者第一次跳两节,
面试题 08.06. 汉诺塔问题(整活版)(不讲武德)
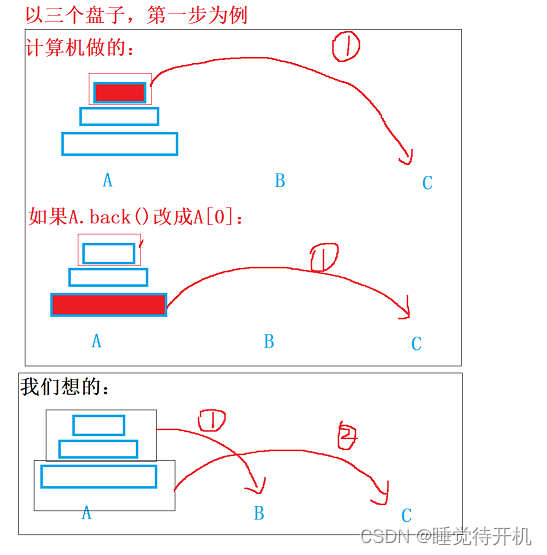
题目具体要求看面试题 08.06. 汉诺塔问题(递归法)-CSDN博客 class Solution {public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {C=A;A.clear();}};
【具体数学 Concrete Mathematics】1.1.1 汉诺塔问题
【具体数学 Concrete Mathematics】1.1.1 汉诺塔问题 汉诺塔问题的设定是:给定一个由8个圆盘 1 − 8 1-8 1−8( 1 1 1号圆盘最小, 8 8 8号圆盘最大)和三根柱子 A , B , C A,B,C A,B,C,从上向下这些圆盘大小逐渐递减(即圆盘不能放在比自身小的圆盘上)放在柱子 A A A上。 问: 最少需要多少步能够将所有圆盘都转移到柱子 C C C
hanno(汉诺塔)问题
汉诺塔是一个经典的函数递归实现的问题 三根柱子,把n片盘子从from柱借助temp柱移动到to柱,可将此过程分为三步: 第一步:将n-1个盘子从from柱借助to柱移动到temp柱 第二步:将第n个盘子从from柱移动到to柱 第三步:将n-1个盘子从temp柱借助from柱移动到to柱 即可完成整个操作 这时我们需要思考的也就是第一步如何实现,第一步的实现方式就是我们整个函数要
汉诺塔问题的java递归实现
import java.util.Scanner;public class Hanoi {int count=0;public void hanoi(int n,char A,char B,char C){ //把n个盘子移动到ccount++;if(n==1){System.out.println("盘子1从"+A+"移动到"+C); //再把最下边那个最大的盘子移到目标柱c上}el
用栈来求解限制后的汉诺塔问题
用栈来求解限制后的汉诺塔问题(限制不能从最左侧的塔直接移动到最右侧,也不能从最右侧直接移动到最左侧,而是必须经过中间,求当塔有N层的时候,打印最优移动过程和最优移动总步数) import java.util.Stack;//用栈来求解限制后的汉诺塔问题(限制不能从最左侧的塔直接移动到最右侧,也不能从最右侧直接移动到最左侧,而是必须经过中间,求当塔有N层的时候,打印最优移动过程和最优移动总步数
分治算法:汉诺塔问题
1,基本介绍 分治算法是一种重要的算法。基本思想就是“分而治之”,将一个复杂的问题分为多个相似的子问题,然后再把子问题分为更小的子问题,直到最后子问题可以以一种最简单的方式直接求解,原问题的解即为子问题解的合并。分治算法的一些经典算法如:二分搜索,棋盘模型,合并排序,快速排序,汉诺塔等,以下将用汉诺塔举例 2,基本步骤 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题解
递归函数-汉诺塔经典递归
前言 最近在读《JavaScript语言精粹》,对递归函数有了进一步的认识,希望总结下来: 递归是一种强大的编程技术,他把一个问题分解为一组相似的子问题,每一问题都用一个寻常解去解决。递归函数就是会直接或者间接调用自身的一种函数,一般来说,一个递归函数调用自身去解决它的子问题。 "汉诺塔"经典递归问题 "汉诺塔"是印度的一个古老传说,也是程序设计中的经典的递归问题,是一个著名的益智游戏:
数据结构之递归小练习(定义,阶乘,求和,汉诺塔)
递归定义;程序直接或间接调用自己,叫做递归。 成为递归的条件:1.要操作的数据规模一直减小,一般而言就是解决n问题必须解决n-1的问题2.必须有一个明确的终止条件。3.每一次的操作都相同,当前的数据和n-1个数据的关系都相同。 小例子: 1.用递归的思想求阶乘: #include<stdio.h> long fn(int n); int main() { int r;
NYOJ93 汉诺塔(三)【栈】
汉诺塔(三) 时间限制:3000 ms | 内存限制:65535 KB 难度:3 描述 在印度,有这么一个古老的传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一
NEFU564 汉诺塔【递归】
题目链接: http://acm.nefu.edu.cn/JudgeOnline/problemshow.php?problem_id=564 题目大意: 庙里有3个柱子,柱A、柱B、柱C。柱A有64个盘子,从上往下越来越大。庙里的老和尚想把这64个盘子 全部移动到柱C上。移动的时候始终只能小盘子压住大盘子,大盘子不能在小盘子上边。每次只能移动一 个。问:将柱A上面钱N个盘子从A
<题海拾贝>[递归]1.汉诺塔
链接 面试题 08.06. 汉诺塔问题 - 力扣(LeetCode) 函数头设计–重复子问题 假设是a,b,c三个柱子,a上面有n个盘子 所以函数头要三个数组,还要知道这次a柱上面的盘子数size 所以函数头如下 void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int size) 函数体设计–某个子问题 步骤: 把
hdu(1997) 汉诺塔VII
若把n个盘子从柱子a通过柱子b移到柱子c,则先把n-1个盘子从柱子a移动柱子b,再把第n个盘子从a移道c,再把n-1个盘子从b移到a。 所以当判断序列是否符合把n个盘子从a移到c时,第n个只能出现在柱子a的最底部,或柱子c的最底部,否则这个序列错的。 当第n个盘子在a的最底部时,则继续判断剩下的序列是否把n-1个盘子从a移到b。 当第n个盘子在c的最底部时,则继续判断剩下的序列是否把n-1个
有关于递归函数的一些学习记录(Recursion)走楼梯,递归找出最两个数的大公约数,汉诺塔问题
递归函数的定义是指在函数执行的过程中,在函数体中直接或间接的调用了自己,这样的函数就是递归函数。递归函数的使用使得分而制之(Divide and Conquer)的思想得意实现,并在解决循环和一些复杂的求解问题中显示了很好的作用。 问题一:说,一个人在爬一个楼梯时,一次可以走一个台阶也可以走两个台阶,问这个人走到第九个台阶有多少种走法? 这是我在2013年春参加南京大学计
python学习之汉诺塔
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老的传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。 问题:有三根柱子(A,B,C),A上有N个圆盘,从底部往上从大到小叠放。将A上的圆盘按以下规则借助B移动到C上
经典算法1:递归求解汉诺塔
题型分析: 算法:当只有一个盘子的时候,只需要从将A塔上的一个盘子移到C塔上。 当A塔上有两个盘子是,先将A塔上的1号盘子(编号从上到下)移动到B塔上,再将A塔上的2号盘子移动的C塔上,最后将B塔上的小盘子移动到C塔上。 当A塔上有3个盘子时,先将A塔上编号1至2的盘子(共2个)移动到B塔上(需借助C塔),然后将A塔上的3号最大的盘子移
【算法】递归、搜索与回溯——汉诺塔
题解:汉诺塔(递归、搜索与回溯算法) 目录 1.题目2.题目背景(拓展了解)3.题解4.参考代码5.细节6.总结 1.题目 题目链接:LINK 2.题目背景(拓展了解) 汉诺塔问题是一个通过隐式使用递归栈来进行实现的一个经典问题,该问题最早的发明人是法国数学家爱德华·卢卡斯。 汉诺塔传说: 传说印度某间寺院有三根柱子,上串64个金盘。寺院里的僧侣依照一个古老的预













![<题海拾贝>[递归]1.汉诺塔](/front/images/it_default.gif)