【算法】递归、搜索与回溯—

【算法】递归、搜索与回溯——汉诺塔

本文主要是介绍【算法】递归、搜索与回溯——汉诺塔，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题解：汉诺塔(递归、搜索与回溯算法)

1.题目

题目链接：LINK
在这里插入图片描述

2.题目背景(拓展了解)

汉诺塔问题是一个通过隐式使用递归栈来进行实现的一个经典问题，该问题最早的发明人是法国数学家爱德华·卢卡斯。

汉诺塔传说：
传说印度某间寺院有三根柱子，上串64个金盘。寺院里的僧侣依照一个古老的预言，以上述规则移动这些盘子；预言说当这些盘子移动完毕，世界就会灭亡。这个传说叫做梵天寺之塔问题（Tower of Brahma puzzle）。但不知道是卢卡斯自创的这个传说，还是他受他人启发。若传说属实，僧侣们需要2^64 − 1步才能完成这个任务；若他们每秒可完成一个盘子的移动，就需要5845亿年才能完成。整个宇宙现在也不过137亿年。这个传说有若干变体：寺院换成修道院、僧侣换成修士等等。寺院的地点众说纷纭，其中一说是位于越南的河内，所以被命名为“河内塔”。另外亦有“金盘是创世时所造”、“僧侣们每天移动一盘”之类的背景设定。佛教中确实有“浮屠”（塔）这种建筑；有些浮屠亦遵守上述规则而建。“汉诺塔”一名可能是由中南半岛在殖民时期传入欧洲的。
在这里插入图片描述

与之相似的一个故事就是“棋盘放大米的故事”：
故事是这样的，最初一位大哥发明了一种玩具叫做围棋，这个围棋有64个格子组成，国王很高兴问发明者什么赏赐，发明者说到“第一个格子放1粒大米，第二个格子放2粒大米，第三个格子放4粒大米，此后每个格子都是前面的两倍大米，放满棋盘上的64个格子就好”，随后国王欣然接受，然而经过实践，即使把整个王国的大米搬过来放，也不能放满64个棋格。
在这里插入图片描述

这两个故事都揭示了一个道理——指数大爆炸。

3.题解

我们枚举不同N情况下移动过程如下：
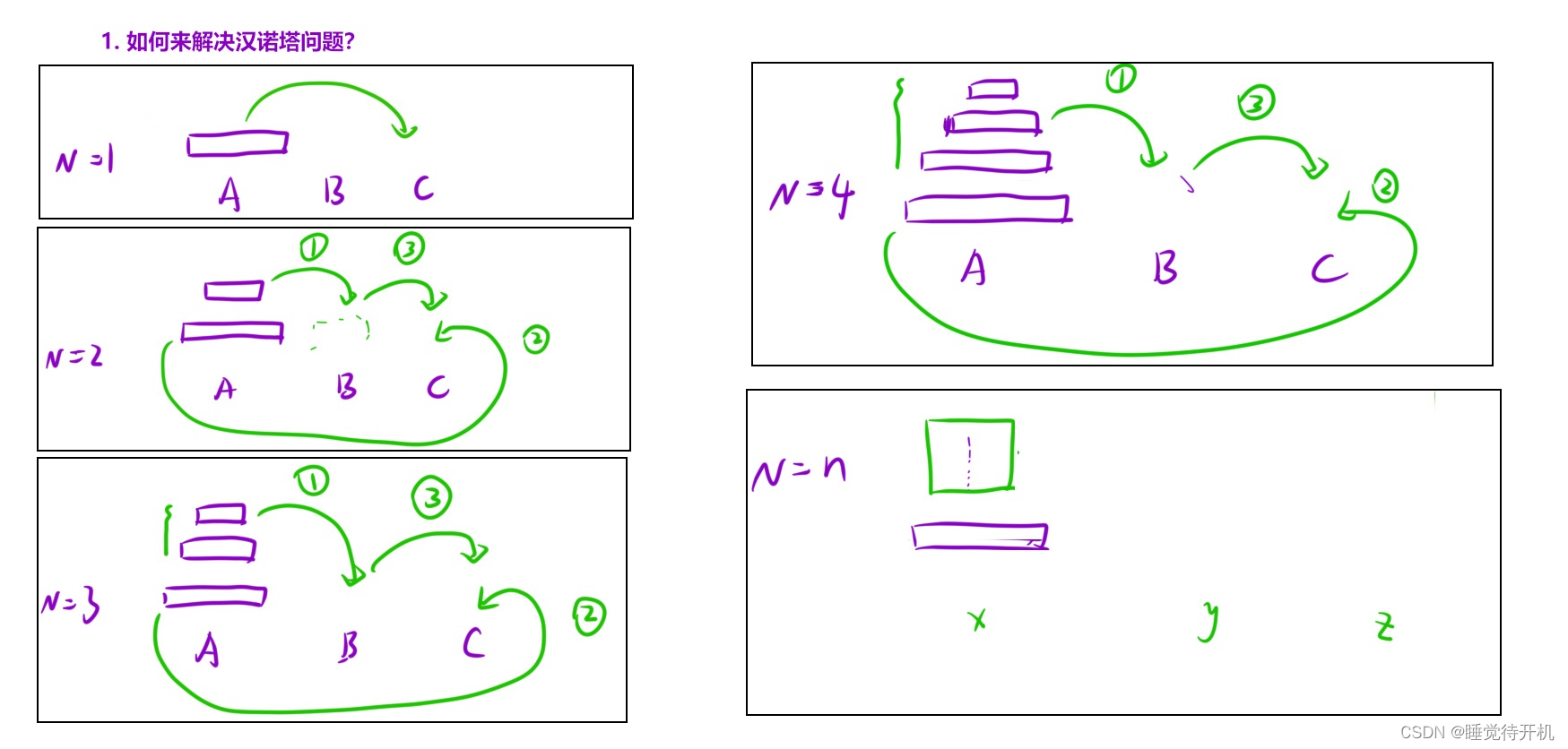
在这里插入图片描述
写递归的步骤

函数头的设计
除N = 1，情况外，所有N的情况都可以分为三步，即先把A柱上的前N-1个盘子放到B柱上，再把A柱的最下面一个盘子放到C上，再把B柱上的盘子放到C上。
所以，解决此问题，我们只需要接受A、B、C、N的个数即可。
函数体的设计
先把A柱上的N-1个盘子放到B柱上，再把A的最下的一个盘子放到C上，再把B上的N-1个盘子放到C上。
函数结束
当N = 1时，不再满足上述三步走规律，只需要把那个盘子放到C上即可。

4.参考代码

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A,B,C,A.size());}void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n){//出递归if(n == 1){C.push_back(A.back());A.pop_back();return;}//1.先把A中的N-1个盘子借助C扔到B上dfs(A,C,B,n-1);//2.再把A中剩下的一个盘子扔到C上C.push_back(A.back());A.pop_back();//3.再把B中的N-1个盘子借助A扔到C上dfs(B,A,C,n-1);}
};

5.细节

思考：
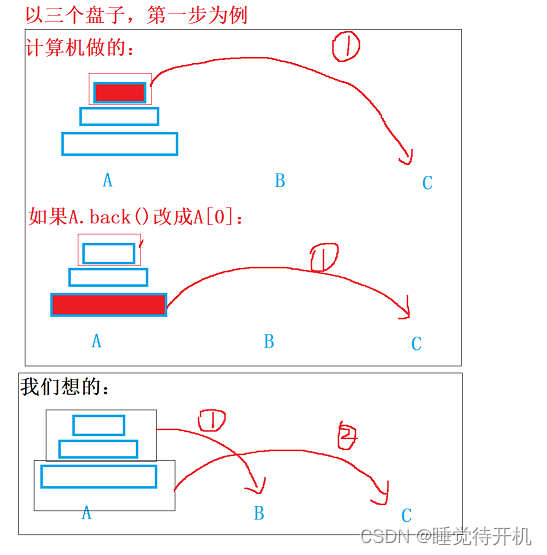
如果我们把代码C.push_back(A.back())改成C.push_back(A[0])可以吗？为什么？

答：不行。 因为我们思考顺序与实际挪动顺序不一致。
虽然我们直觉上认为A.back()与A[0]在只剩下一个元素时候都表示的是最后的那个盘子，但是计算机运行的顺序跟我们脑子想的顺序并不一致，计算机先从最小的子问题(不可分割)的情况开始运算，而我们想的是先从最大问题的那个开始思考。
在只剩下一个元素的情况下A[0]和A.back()的确是一样的，但是计算机运行的时候并不是只有一个元素！！！

举个例子：
在这里插入图片描述