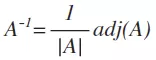求逆专题

【SGU】180. Inversions（归并排序求逆序数）

以前一般用树状数组和线段树做这种题这次换个思路试试，归并排序！ #include<cstdio>#include<cstring>#include<algorithm>using namespace std;typedef long long LL;const int maxn = 111111;int n;int array[maxn];int tmp[maxn];L

归并求逆序数对

c# bobo bobo 慢慢分析中 public class Solution {public int ReversePairs(int[] nums) {int[] temp = new int[nums.Length];Array.Copy(nums, 0, temp, 0, nums.Length);return Sort(nums, 0, nums.Length -

HDU 1541 Stars || POJ 2352 stars || NYOJ 117 求逆序数

题目链接~~> 做题感悟：其实都是求逆序数，但是NYOJ 数特别大，需要离散化一下。解题思路：HDU || POJ 上的 stars 求左下角有多少个星星，因为是按 y 值递增排好序的,so 只要前面的点的 x 坐标小于等于当前 x 坐标的就可以了。查找时向下查找，更新时向上更新。NYOJ 那题因为数特别大，需要离散化一下（切记排序时要稳定排序），只要用下表减去查找到有几个比它小的就可以了。

Sweet Snippet 之矩阵求逆

矩阵求逆的简单实现矩阵求逆有很多种方法,使用伴随矩阵可能是相对易于编码的方式,在此简单列一下实现(Lua): -- matrix store is table in row order-- e.g. 2 x 2 matrix is stored as table { m11, m12, m21, m22 }-- determinant 2 with scalar elementsf

伴随矩阵求逆矩阵

在之前的文章《线性代数之矩阵》中已经介绍了一些关于矩阵的基本概念，本篇文章主要就求解逆矩阵进行进一步总结。余子式(Minor) 我们先看例子来直观的理解什么是余子式(Minor，后边将都用英文Minor，中文的翻译较乱）。 minor example 这个例子（我们假设矩阵为A）中我们看到A[1,1]的minor就是将A[1,1]所在的行和列删除后剩下的矩阵的行列式，假设我们把A[

树状数组求逆序数 poj 2299 离散化

树状数组求逆序数 poj 2299 这里说的很好，把求逆序的步骤说的很明白，我也是看完才懂的，之前自己想了很久就是不明白为什么可以用树状数组求逆序　　转载：树状数组，具体的说是离散化+树状数组。这也是学习树状数组的第一题. 算法的大体流程就是： 1.先对输入的数组离散化，使得各个元素比较接近，而不是离散的， 2.接着，运用树状数组的标准操作来累计数组的逆序数。算法详细解释

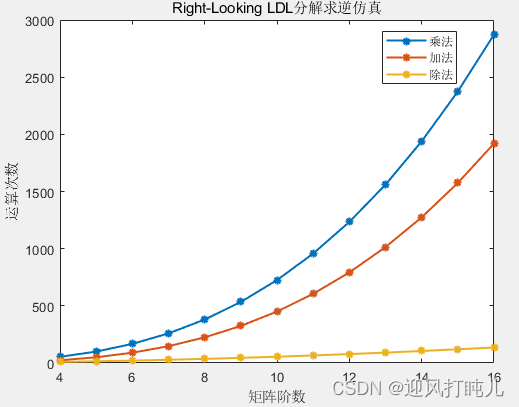
LDL^H分解求逆矩阵与MATLAB仿真(Right-Looking)

通过分解将对称正定厄米特矩阵分解成下三角矩阵L和对角矩阵D来求其逆矩阵目录前言一、LDL^H基本算法二、LDL^H Right-Looking算法三、D矩阵求逆四、L矩阵求逆五、A矩阵求逆六、计算量分析七、MATLAB仿真八、参考资料总结前言在线性代数中，LDL^H分解是将一个矩阵分解为一个下三角矩阵（L）与一个

c#矩阵求逆

目录一、矩阵求逆的数学方法 1、伴随矩阵法 2、初等变换法 3、分块矩阵法 4、定义法二、矩阵求逆C#代码 1、伴随矩阵法求指定3*3阶数矩阵的逆矩阵（1）伴随矩阵数学方法（2）代码（3）计算 2、对任意阶数矩阵求逆（1）计算方法（2）代码（3）计算（4）计算结果三、工程下载连接一、矩阵求逆的数学方法 1、伴随矩阵法 2、初等

Divide and ConquerCount Inversions归并排序求逆序数

Divide and Conquer The attached le Q8.txt contains 100,000 integers between 1 and 100,000 (each row has a single integer), the order of these integers is random and no integer is repeated. 刚写程序是用的

D. Yet Another Sorting Problem - 树状数组求逆序数

题面分析选三个下标，如果能够将这三个下标换成排好序的数，那么一定是逆序数为2或者-2，所以对于整体来说，只要是逆序数个数为偶数就可以实现，其次，如果有两个相同的数存在，那么一定可以实现排序，每次都可以将两个相同的数放到正确的位置。代码 #include <bits/stdc++.h>using namespace std;using ll = long long;void solv

python C++ 求逆矩阵库

python求逆矩阵库 https://numpy.org/ C++求逆矩阵库 http://eigen.tuxfamily.org/index.php?title=Main_Page

c++实现任意矩阵求逆

关于矩阵求逆记忆最深的就是在静宜大学参加程序比赛，这是遇见的第一个问题。刚才突然想到，于是又百度Google了一番，又有了下面这篇水文~ 　　矩阵的求逆按矩阵类型分2种，一种是方阵，一种就是任意的矩阵了。而求逆的过程，我们学过线数就知道，可以用行列变化，用伴随矩阵。两种思路的代码网上都有，这里贴出一部分c++写的代码，是针对任意矩阵的用伴随的方法（先求代数余子式）。完全的代码和矩阵类，等我会

雅克比矩阵求逆的几种情况

1. 常规雅克比矩阵的逆根据关节角度，可得末端速度方程： v e = J ( q ) q ˙ v_e=J(q)\dot q ve=J(q)q˙ 如果雅克比矩阵式方阵且可逆，可得关节速度为 q ˙ = J − 1 ( q ) v e \dot q=J^{-1}(q)v_e q˙

poj2299解题报告（归并排序求逆序数）

POJ 2299，题目链接http://poj.org/problem?id=2299 题意：给出长度为n的序列，每次只能交换相邻的两个元素，问至少要交换几次才使得该序列为递增序列。思路：其实就是求逆序数，那么直接向到的就是冒泡了，交换一次，记录一次即可。但是n的范围达到50W，冒泡O(n^2)的复杂度铁定超时。然后、、、发现曾经微软有一道笔试题类似就是求逆序数的，对

线段树--求逆序数

求逆序数，n<= 50000,ai < 1e9 oredr记录数字大小和顺序位置，sort后，对每个数，求比他小（即排序后在他前面的），但是原位置比他大（即order[j].second比他的order[i].second大）的数的个数，（线段树记录数的个数，在线段树总存入order[i].second即可得到）。 #include <iostream> #include <cstd

http://acm.nyist.net/JudgeOnline/problem.php?pid=117树状数组求逆序数+离散化

这一题一开始是胸有成竹的，本想1A的，但是接二连三的wa了好几次。。。把我满满的自信心消磨殆尽了。。我一遍一遍的寻找错误，就是找不到。。最后实在没办法要了后台的数据。。运行一看。令我大跌眼眶。。。。竟然都对了，，但为什么WA呢？可能是这一题判题写错了？，最后在不抱希望的情况下我把%I64d改成了%lld，竟然AC了，苦逼的孩子。。oj竟然不支持%I64d..... AC代码： #inclu

【模板】矩阵求逆

方法就是通常的那种方法，就是在原矩阵旁边放一个单位矩阵，对两个矩阵一起高斯消元，当原矩阵被消成单位矩阵时右边的单位矩阵就是它的逆，在高斯消元过程中如果不能继续下去就无解步骤就是先找到当前要操作的行，然后给这一行进行变换，乘以 1 f i , i \frac{1}{f_{i,i}} fi,i1 然后对其余行，给操作行乘以 − f j , i -f_{j,i} −fj,i加到这些行上去，这样

数学_矩阵求逆/伪逆计算

目录 1. 求位姿矩阵T的逆 2. 几种常见的特殊矩阵的求逆 2x2矩阵求逆对角矩阵求逆

poj2299Ultra-QuickSort(归并求逆序数)

Ultra-QuickSort 时间限制:7000毫秒内存限制:65536 k总提交:54431年接受:20001年描述在这个问题上,你必须分析一个特定的排序算法。 n截然不同的整数的算法流程序列通过交换两个相邻序列元素,直到序列按升序排序。输入序列 9 1 0 5 4, Ultra-QuickSort生成的输出 1 4 5 0 9。