欧氏专题
k近邻(kNN)算法的Python实现(基于欧氏距离)
k近邻算法是机器学习中原理最简单的算法之一,其思想为:给定测试样本,计算出距离其最近的k个训练样本,将这k个样本中出现类别最多的标记作为该测试样本的预测标记。 k近邻算法虽然原理简单,但是其泛华错误率却不超过贝叶斯最有分类器错误率的两倍。所以实际应用中,k近邻算法是一个“性价比”很高的分类工具。 基于欧式距离,用Python3.5实现kNN算法: 主程序: from numpy impor
轨迹优化 | 图解欧氏距离场与梯度场算法(附ROS C++/Python实现)
目录 0 专栏介绍1 什么是距离场?2 欧氏距离场计算原理3 双线性插值与欧式梯度场4 仿真实现4.1 ROS C++实现4.2 Python实现 0 专栏介绍 🔥课程设计、毕业设计、创新竞赛、学术研究必备!本专栏涉及更高阶的运动规划算法实战:曲线生成与轨迹优化、碰撞模型与检测、多智能体群控、深度强化学习运动规划、社会性导航、全覆盖路径规划等内容,每个模型都包含代码实现加深理
计算欧氏距离cvNorm
Norm 计算数组的绝对范数, 绝对差分范数或者相对差分范数 double cvNorm( const CvArr* arr1, const CvArr* arr2=NULL, int norm_type=CV_L2, const CvArr* mask=NULL ); 参数: arr1 第一输入图像 arr2 第二输入图像 ,如果为空(
【No.20】蓝桥杯简单数论下|寻找整数|素数的判断|笨小猴|最大最小公倍数|素数筛|埃氏筛|欧氏线性筛|质数|分解质因子(C++)
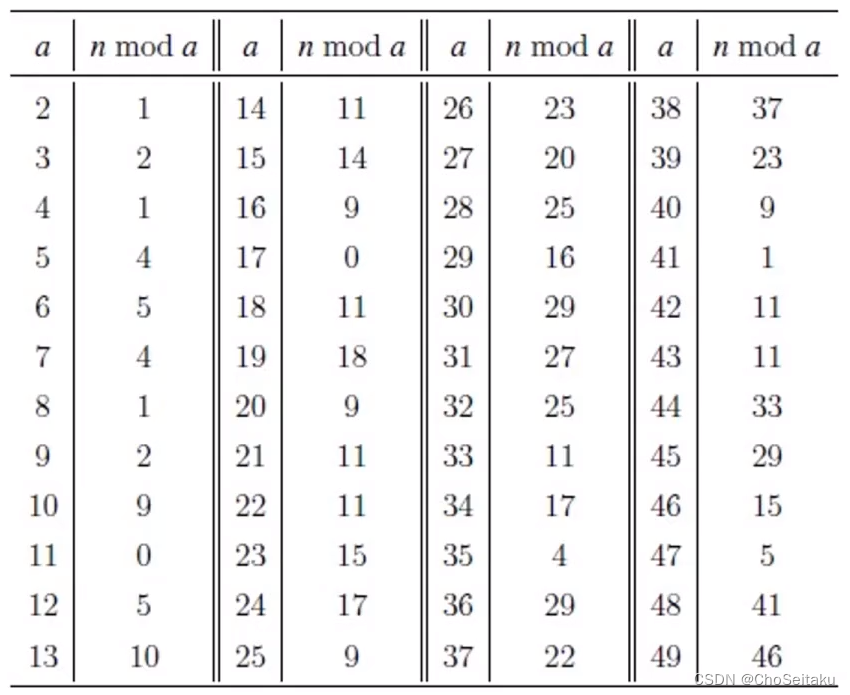
寻找整数 【题目描述】 有一个不超过 1 0 1 7 10^17 1017的正整数n,知道这个数除以2至49后的余数如下表所示,求这个正整数最小是多少 解法一:模拟 暴力法:一个个检验 1 … 1 0 17 1\dots 10^{17} 1…1017的每个数 由于这个数n最大可能是 1 0 17 10^{17} 1017,验证的时间太长 解法二:LCM 从表格的第一个数2开始,逐个增加
欧氏、相似、防射、射影变换
3D空间中的变换有:欧氏变换、相似变换、防射变换、射影变换。 欧氏变换:最简单的变换,它保持了向量的长度和夹角,相当于把一个刚体原封不动的移动或者旋转。 相似变换:比欧氏变换多一个自由度,它允许对物体进行均匀的缩放。 防射变换:又叫正交投影,经过变换后,立方体不再是方的,但是各个面仍是平行四边形。 射影变换:最一般的变换。例如使用相机随意拍摄一个方形的地板砖,在照片中的样子,它不再是方的,
[推荐系统]欧氏距离和余弦相似度
两者相同的地方,就是在机器学习中都可以用来计算相似度,但是两者的含义有很大差别,以我的理解就是: 前者是看成坐标系中两个点,来计算两点之间的距离; 后者是看成坐标系中两个向量,来计算两向量之间的夹角。 前者因为是点,所以一般指位置上的差别,即距离; 后者因为是向量,所以一般指方向上的差别,即所成夹角。 如下图所示: 数据项A和B在坐标图中当做点时,两
【python】 计算向量欧氏距离的小代码 numpy
给定两个向量,计算欧式距离 直接调用numpy中的几个函数就行了 这种东西,绝对不要自己写,哈哈 涉及到怎么将list转化为numpy的array def calEuclideanDistance(vec1,vec2):dist = numpy.sqrt(numpy.sum(numpy.square(vec1 - vec2)))return
欧氏距离,曼哈顿距离,夹角余弦距离,切比雪夫距离,汉明距离,闵可夫斯基距离,马氏距离
目录 1.欧式距离EuclideanDistance 2. 曼哈顿距离(ManhattanDistance) 3. 夹角余弦 4.汉明距离(Hamming Distance) 1.欧式距离EuclideanDistance 欧式距离:也称欧几里得距离,在一个N维度的空间里,求两个点的距离,这个距离肯定是一个大于等于零的数字,那么这个距离需要用两个点在各自维度上的坐标
[点云分割] 条件欧氏聚类分割
介绍 条件欧氏聚类分割是一种基于欧氏距离和条件限制的点云分割方法。它通过计算点云中点与点之间的欧氏距离,并结合一定的条件限制来将点云分割成不同的区域或聚类。 在条件欧氏聚类分割中,通常会定义以下两个条件来判断两个点是否属于同一个聚类: 距离条件:两个点之间的欧氏距离是否小于设定的阈值。如果两个点之间的距离小于阈值,则认为它们是相邻的,属于同一个聚类。 条件限制:除了距离条件外,还可以根据
SQL2008空间数据类型--欧氏几何1基础
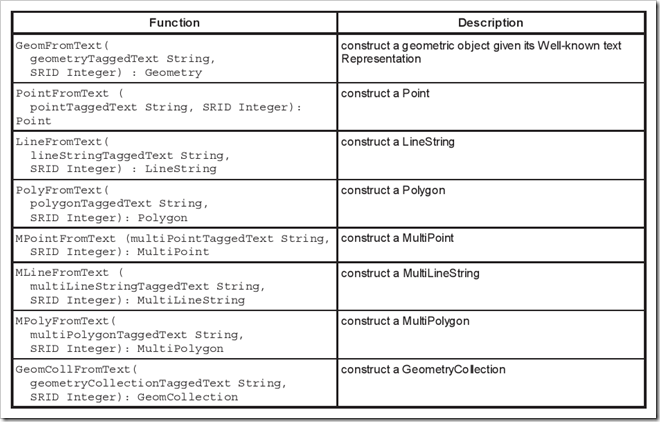
1 基础 在SQL2008中增加了对地理空间数据类型的支持,该类型分为2种:欧式(平面)几何geometry 和地理空间(椭圆体)几何geography 。欧式几何大家基本上都学过,是以坐标来表示,而地理空间就是使用经度和纬度来表示,由于平面几何比较简单(我记得好像是初中时候学的,高中学立体几何),所以我就从简单的学起,先学习geometry 数据类型。 在平面几何中我们有3个基本元素:点、线、
人工智能基础_机器学习022_使用正则化_曼哈顿距离_欧氏距离_提高模型鲁棒性_过拟合_欠拟合_正则化提高模型泛化能力---人工智能工作笔记0062
然后我们再来看一下,过拟合和欠拟合,现在,实际上欠拟合,出现的情况已经不多了,欠拟合是 在训练集和测试集的准确率不高,学习不到位的情况. 然后现在一般碰到的是过拟合,可以看到第二个就是,完全就把红点蓝点分开了,这种情况是不好的, 因为分开是对训练数据进行分开的,如果来了测试数据他的效果就不好了,也就说,泛化能力不行. 然后最理想的是第三个图. 可以看到如果我们有一个2图中的绿
Atitti knn实现的具体四个距离算法 欧氏距离 余弦距离 汉明距离 曼哈顿距离
Atitti knn实现的具体四个距离算法 欧氏距离、余弦距离、汉明距离、曼哈顿距离 1.Knn算法实质就是相似度的关系1 1.1.文本相似度计算在信息检索、数据挖掘、机器翻译、文档复制检测等领域有着广泛的应用1 2.汉明距离1 2.1.历史及应用1 3.曼哈顿距离2 3.1.SimHash + 汉明距离3 3.2.、简单共有词4 1. Knn算法实质就是相似度的关系 1.1.




![[推荐系统]欧氏距离和余弦相似度](https://img-blog.csdn.net/20130715222725843?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvbGludm8=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)
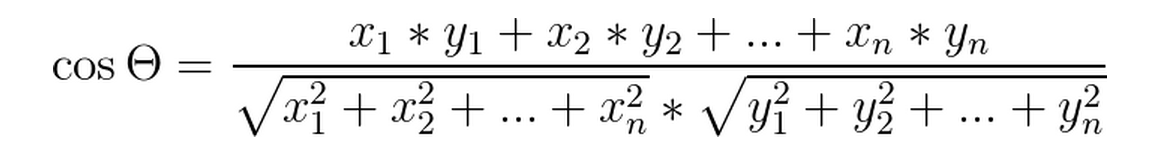
![[点云分割] 条件欧氏聚类分割](https://img-blog.csdnimg.cn/e9ca0fe1d5824918a7b508ee5621ccc4.png)