SQL2008空间数据类型--欧氏几何1基础

1 基础

在SQL2008中增加了对地理空间数据类型的支持，该类型分为2种：欧式（平面）几何geometry 和地理空间（椭圆体）几何geography 。欧式几何大家基本上都学过，是以坐标来表示，而地理空间就是使用经度和纬度来表示，由于平面几何比较简单（我记得好像是初中时候学的，高中学立体几何），所以我就从简单的学起，先学习geometry 数据类型。

在平面几何中我们有3个基本元素：点、线、面。对应的在geometry 数据类型中也是这3种类型Point、LineString、Polygon以及各自的集合MultiPoint、MultiLineString、MultiPolygon 另外还有一个它们的混合的集合GeometryCollection，混合集合中可以包含多个Point多个LineString和多个Polygon。很容易看出MultiPoint、MultiLineString、MultiPolygon是GeometryCollection的一种特殊情况。官方给出的它们的关系如图：

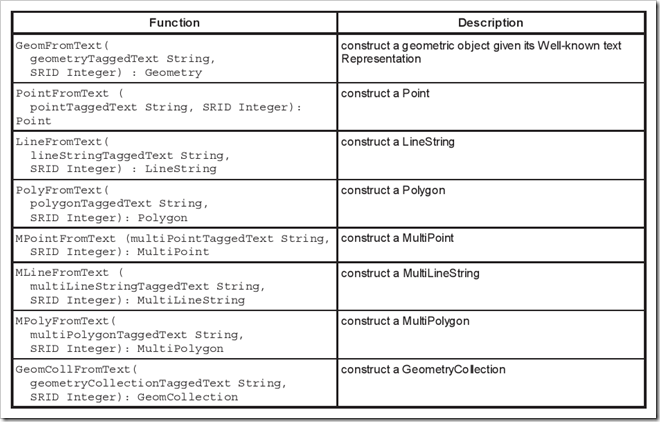
当需要申明一个geometry 对象时需要使用它提供的一个函数STGeomFromText将字符串形式的申明转换为对象。例如要申明一个Point，坐标为1，2 对应的SQL语句就是：

DECLARE @g geometry;
SET @g = geometry::STGeomFromText('POINT (1 2)', 0);
SELECT @g.ToString();

这里Point除了接受x y这2个参数外，还可以接受Z（仰角elevation）和 M（度量measure）值，在平面几何中好像没有这个概念啊？不知道是拿来做什么用的，估计是在地理数据类型中才会使用吧。

除字符串之外，STGeomFromText还有一个参数就是SRID。SRID是空间引用标识符的简称，主要用于地理数据类型，在平面几何数据类型中SRID默认是0，关于SRID的具体作用在地理数据类型的时候再研究，只需要知道，不同SRID的2个实例是不能进行运算的，运算的结果都是NULL。

这里的POINT(1 2)字符串是必须符合熟知文本（Well-Known Text，WKT）的格式。点、线、面和对应集合等的字符串申明如：

• POINT(1 2)定义一个点
• LineString(1 2,1 4,2 4,3 5)定义一折线
• POLYGON((0 0, 0 3, 3 3, 3 0, 0 0))定义一个多边形，POLYGON((0 0, 0 3, 3 3, 3 0, 0 0),(1 1, 1 2, 2 1, 1 1))定义一个带孔的多边形
• MultiPoint((1 2),(1 3),(1 4))定义了3个点的点集合
• MultiLineString((1 2,1 3),(1 4,2 4, 4 4))定义了2条线的线集合
• MultiPolygon(((0 0, 0 3, 3 3, 3 0, 0 0), (1 1, 1 2, 2 1, 1 1)), ((9 9, 9 10, 10 9, 9 9)))定义了一个带孔多边形和另一个实心多边形的面集合
• GeometryCollection(POLYGON((0 0, 0 3, 3 3, 3 0, 0 0), (1 1, 1 2, 2 1, 1 1)), Point(9 9))定义了一个带孔多边形和一个点的集合

STGeomFromText太长了不好记也不好打，还是使用另外一个函数Parse安逸。Parse函数只有一个参数，就是符合WKT的字符串，不需要指定SRID，申明一个点可以写为：

SET @g = geometry::Parse('POINT (1 2)');

这里WKT字符串是不区分大小写的，但是由于空间数据类型是CLR定义出来的，可以理解为是用C#写的一个数据类型，所以在使用的时候是要区分大小写的，不能写成parse('POINT(1 2)')了！

既然可以从字符串转换为几何对象，那么肯定也有办法将几何对象转换为字符串，SQL中提供了2个函数实现该功能：STAsText()和ToString()。这两个函数的区别就在于ToString除了坐标外还返回了对象中的仰角和度量（如果定义了的话），而STAsText是只返回定义中的坐标。

今天学了对平面几何类型的定义，下次就开始学习使用了。