欧几里德专题
欧几里德算法(幂运算)
文中X(N) 表示X的N次方; 计算X(N) 的明显算法是使用N-1次乘法自乘,有一种递归算法更好:N≤1是这种递归的基准情形,否则若N为偶数,我们有X(N) = X(N/2) × X(N/2),若X为奇数,则X(N) = X((N-1)/2) × X((N-1)/2) × X 例如:为了计算X(62),算法将如下进行,它只用到9次乘法: X(6
欧几里德算法(求两数最大公因数)
两个整数的最大公因数(gcd)是同时整除两个大最大整数。即gcd(50,15)=5. 算法连续计算余数直到除数为0,最后的非0余数就是最大公因数。因此若M=1989,N=1590,则余数是399,393,6,3,0,从而gcd(1989,1590)=3,这是一个快速算法。 public static long gcd(long m,long n){ while(n !
再说中国剩余定理、扩展欧几里德和同余方程组
E - 解同余线性方程组1 Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit Status Description Andy和Mary养了很多猪。他们想要给猪安家。但是Andy没有足够的猪圈,很多猪只能够在一个猪圈安家。举个例子,假如有16头猪,An
再说中国剩余定理、扩展欧几里德与同余方程组
E - 解同余线性方程组1 Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit Status Description Andy和Mary养了很多猪。他们想要给猪安家。但是Andy没有足够的猪圈,很多猪只能够在一个猪圈安家。举个例子,假如有16头猪,A
POJ-1061 青蛙的约会-数论扩展欧几里德算法入门及推导
Description 两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳,直到碰面为止。可是它们出发之前忘记了一件很重要的事情,既没有问清楚对方的特征,也没有约定见面的具体位置。不过青蛙们都是很乐观的,它们觉得只要一直朝着某个方向跳下去,总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上,不然是永远都不可能碰面的
UVA10717 - Mint(欧几里德求最小共倍数)
UVA10717 - Mint(欧几里德求最小共倍数) 题目链接 题目大意:要求你设计桌子,桌子的四条腿是用四种不同的硬币堆砌起来,并且这四条腿的长度要求要种相同。现在给n种硬币,然后给你t个要求的高度H。要求你给出能够用这些硬币设计出来的桌子的高度最接近H的两个数。 解题思路:要求四条腿一样长的话就是求这四种硬币厚度的最小共倍数,然后这里会给n种硬币,需要枚举出每四个的组合,求出用
nefu 84 五指山(扩展欧几里德)
五指山 Problem : 84 Time Limit : 1000ms Memory Limit : 65536K description 西游记中孙吾空大闹天宫,如来佛祖前来降伏他,说道:“我与你打个赌赛;你若有本事,一筋斗打出我这右手掌中,算你赢,再不用动刀兵苦争战,就请玉帝到西方居住,把天宫让你;若不能打出手掌,你还下界为妖,再修几劫,却来争吵。”那
SGU 106. The equation 扩展欧几里德
求解的个数 对应ax+by=c 根据裴蜀定理c%gcd(a, b) == 0有解 假设d = gcd(a, b) 用扩展欧几里德求出方程aax+bb*y=cc 的解x0 y0 那么原方程的一个解就是x0*c/d和y0*c/d 通解为 x = x0+i*b/d y = y0+i*a/d 分别讲x1 x2 带入得到i 满足最小的左区间 y1 y2一样 #include <cstd
欧几里德算法 求最大公约数
欧几里德算法 gcd, 最大公因式 (greatest common divisor) 证明: 欧几里德算法又称 辗转相除法,用于计算两个 正整数a,b的 最大公约数。其计算原理依赖于下面的定理: 定理:gcd(a,b) = gcd(b,a mod b) (a>b 且a mod b 不为0) 证明:a可以表示成a = kb + r,则r = a mod b 假设
数论基础 辗转相除 扩展欧几里德
辗转相除: 辗转相除,又称为欧几里德算法,用于求解俩个数值的最大公约数,原理如下: gcd(a,b) = gcd(b,a%b) = gcd(a%b,(a%b)%b) ... = gcd(c,0) = c; 一般经过俩次的递归之后,第一个参数就小于原来的一半,所以不用但是栈溢出的情况。 int gcd(int a,int b){if(b==0)return a;return
hdu1576 A/B(扩展的欧几里德算法)
A/B Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 1369 Accepted Submission(s): 1045 Problem Description 要求(A/B)%9973,但由于A很大,我们
相似度的算法(欧几里德距离和皮尔逊算法)
给了我两个东西,每个东西上有不同的特征,那咱们就算算这两个东西的相似的系数吧 先说欧几里德距离,按几何意义来讲就是按n个特征给它建立起来n维坐标系,就先说二维吧,二维上就是两个点咯,xy轴,这两个点相似否,就看他的距离咯,于是 就求一下两个点的距离,三个特征呢?那就是三维坐标系。由此推广,可以推广到n维。 公式:|x| = √( x[1]2 + x[2]2 + … + x[n]2 ) 欧式
【ACM】欧几里德算法
欧几里德算法又称辗转相除法,用于计算两个正整数a,b的最大公约数。 定理:两个整数的最大公约数等于其中较小的那个数和两个数相除余数的最大公约数。 gcd(a,b) = gcd(b,a mod b) 上述表达式中a>b。限制gcd(a,b) = gcd(|a| , |b|),也就是对非负整数进行了讨论。 证明方法: (百度百科:a可以表示成a = kb + r(a,b,k,r皆为正整数),
关于扩展欧几里德的两道题
ax+by=gcd(a,b) 扩展欧几里得求出的x,y一定互质? 本质都是在通解中找flag的问题 某个dasctf # assert# -148433821482647484270485846381922123996708944085*m1+183523900521399172553866274807303305996926745051*m2==1# solvex=-14843382
P1082 同余方程 扩展欧几里德算法 C++
题目描述 求关于x xx的同余方程 ax≡1(modb) a x \equiv 1 \pmod {b}ax≡1(modb) 的最小正整数解。 输入格式 一行,包含两个正整数 a,b,用一个空格隔开。 输出格式 一个正整数 x0,即最小正整数解。输入数据保证一定有解。 输入输出样例 输入 #1 3 10 输出 #1 7 说明/提示 【数据范围】 对于 40%的数据,2≤b≤1,00
基于欧几里德距离的K最近邻(KNN)算法的实现(JAVA版)
K邻近(k-Nearest Neighbor,KNN)分类算法是最简单的机器学习算法了。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单:计算一个点A与其他所有点之间的距离,取出与该点最近的k个点,然后统计这k个点里面所属分类比例最大的,则点A属于该分类。 下面用一个例子来说明一下: 电影名称 打斗次数 接吻次数 电影类型 California Man
Sicily1099-Packing Passengers-拓展欧几里德算法
最终代码地址:https://github.com/laiy/Datastructure-Algorithm/blob/master/sicily/1099.c 做这题的时候查了别人的做法花了半天都没搞明白怎么做的,我认为别的博客写的难以让人理解所以就造了这个轮子。 题目: 1099. Packing Passengers Constraints Time Limit: 1 secs, Me
Python和NetworkX计算有向图节点欧几里德距离最短路径
Networkx NetworkX 是一个 Python 语言软件包,用于创建、操作和研究复杂网络的结构、动力学和功能。 它用于研究以具有节点和边的图形式表示的大型复杂网络。 使用networkx我们可以加载和存储复杂的网络。 我们可以生成多种类型的随机和经典网络、分析网络结构、构建网络模型、设计新的网络算法和绘制网络。 创建节点 一次添加一个节点: G.add_node(1) 添加节
青蛙的约会 扩展的欧几里德算法
青蛙的约会 Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 127383 Accepted: 27617 Description 两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳,直到碰面为止。可是它们出发之前忘记了一件很重要的事情,
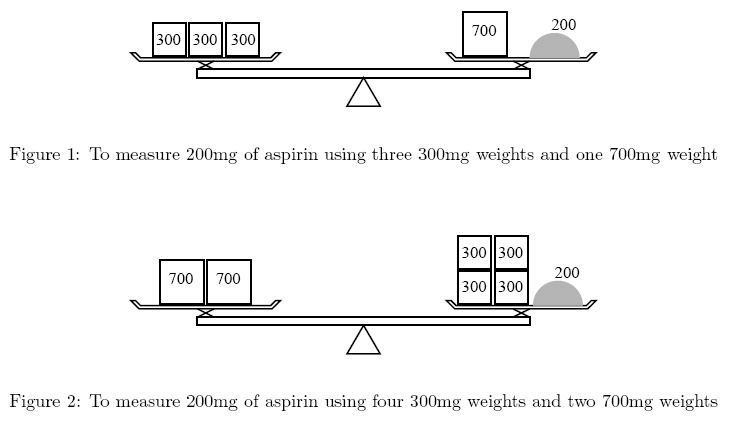
Problem F:The Balance(扩展欧几里德)
POJ2142http://poj.org/problem?id=2142 扩展欧几里德+(x+y)取最小 Description Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of
初等数论以及欧几里德定理的证明
欧几里德定理(无限质数定理) 质数的个数是无限的吗?还是说存在一个最大的质数,比它大的任何数字都可以表示为已有质数的乘积?首先提出这个问题的正式欧几里得本人,他以一种简单而优雅的方式证明了质数有无穷多个,所以并不存在所谓的”最大质数”。为了验证这个命题,我们暂且假设质数的个数是有限的,并用字母N来达标已知最大的质数。现在我们将所有质数相乘,最后再加1,数学表达式如下: 这个式子得出的结果当
洛谷 P1290 欧几里德的游戏
题目描述 欧几里德的两个后代Stan和Ollie正在玩一种数字游戏,这个游戏是他们的祖先欧几里德发明的。给定两个正整数M和N,从Stan开始,从其中较大的一个数,减去较小的数的正整数倍,当然,得到的数不能小于0。然后是Ollie,对刚才得到的数,和M,N中较小的那个数,再进行同样的操作……直到一个人得到了0,他就取得了胜利。下面是他们用(25,7)两个数游戏的过程: Start:25 7 S