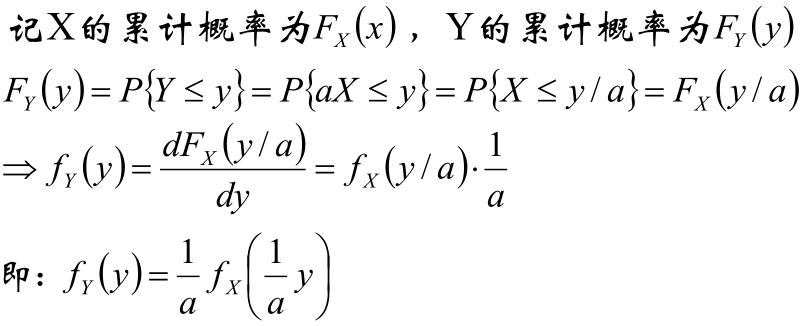概率密度专题
概率论(三)-多维随机变量及其分布:n维随机变量、概率分布函数F(x1,x2,..xn)、联合分布律、联合概率密度、边缘分布律、边缘概率密度、条件分布律、条件概率密度、β函数、Γ函数、max{X,Y}
1 二维随机变量 2 边缘分布 3 条件分布 4 相互独立的随机变量 5 两个随机变量的函数的分布
概率论(二)-随机变量及其分布:分布函数F(x)、离散型随机变量【分布律:(0-1)分布、二项分布、泊松分布】、连续型随机变量【概率密度:均匀分布、指数分布、正态/高斯分布】、3σ法则、偏度、峰度
1 随机变量 2 离散型随机变量及其分布律 3 随机变量的分布函数 4 连续型随机变量及其概率密度 5 随机变量的函数的分布
MATLAB概率密度估计有关的函数
参数估计 mle Maximum likelihood estimates mle是有偏估计 fitdist 对数据进行概率分布对象拟合 histfit 具有分布拟合的直方图 fitdist和histfit是无偏估计,这两者区别在于histfit直接画出直方图。 支持的分布点这里 非参数估计 ksdensity Kernel smoothing function estimate for u
再次思考Z = X+Y,Z = XY的概率密度求解
再次思考Z = X+Y,Z = XY的概率密度求解 @(概率论) 设方程 x2−Xx+Y=0 x^2-Xx+Y = 0的根相互独立,且都在(0,2)上服从均匀分布,分别求X与Y的概率密度。 分析:在前面一篇特别总结过这类题型的解法。 http://blog.csdn.net/u011240016/article/details/53097048 但是这里的题目提示我要注意变量取值的
Z=X+Y型概率密度的求解
###Z=X+Y型概率密度的求解### @(概率论) Z = g ( X , Y ) Z = g(X,Y) Z=g(X,Y) 总结过一次,一般方法是可以由分布函数再求导得到概率密度,计算一定更要小心才能得到正确的解。 F Z ( z ) = P ( Z ≤ z ) = P ( g ( X , Y ) ≤ z ) = ∫ ∫ g ( x , y ) ≤ z f ( x , y ) d x
连续型三种典型概率分布(概率密度)
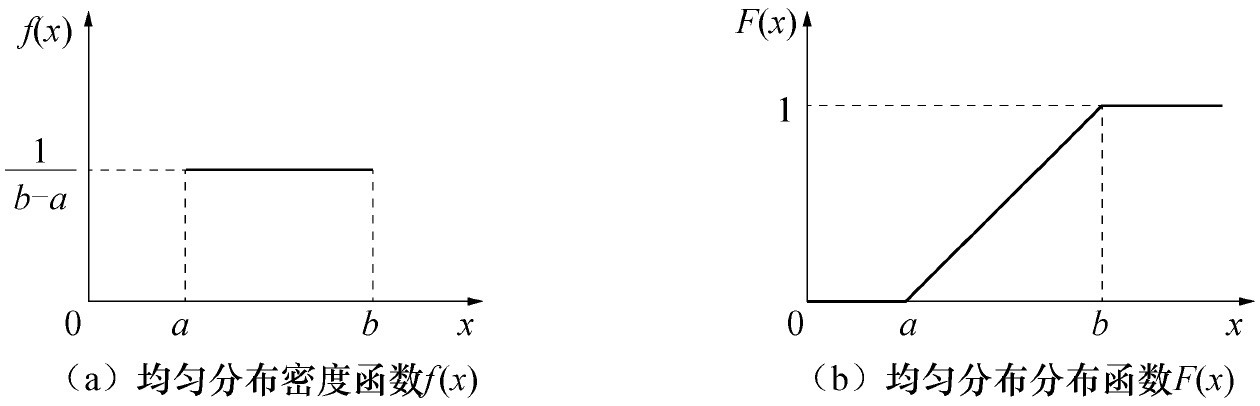
一,均匀分布 二,指数分布 三,正态分布 参考博客:https://blog.csdn.net/u010916338/article/details/81331862
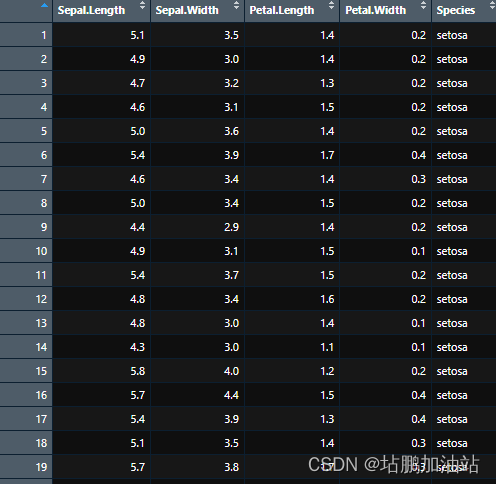
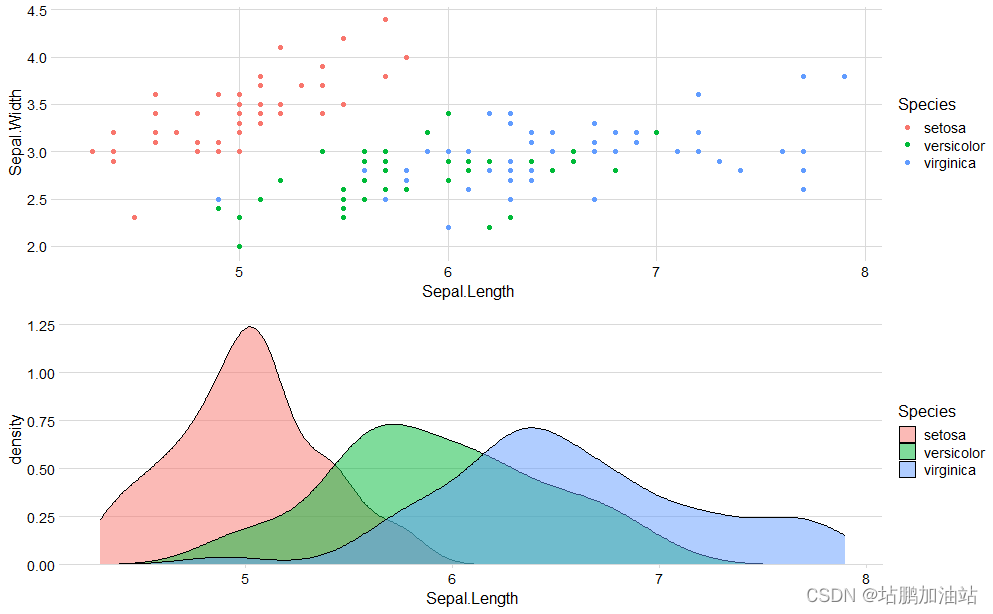
【R语言】边缘概率密度图
边缘概率密度图是一种在多变量数据分析中常用的图形工具,用于显示每个单独变量的概率密度估计。它通常用于散点图的边缘,以便更好地理解单个变量的分布情况,同时保留了散点图的相关性信息。 在边缘概率密度图中,每个变量的概率密度估计通常通过直方图或核密度估计(KDE)进行计算。直方图将变量的值范围分成若干个区间,并统计每个区间中观察值的数量,然后将数量除以总观察值数量得到概率密度。而核密度估计则是
【R语言】概率密度图
概率密度图是用来表示连续型数据的分布情况的一种图形化方法。它通过在数据的取值范围内绘制一条曲线来描述数据的分布情况,曲线下的面积代表了在该范围内观察到某一数值的概率。具体来说,对于给定的连续型数据,概率密度图会使用核密度估计(Kernel Density Estimation,KDE)等方法来估计数据的概率密度函数。然后,在数据的取值范围内绘制一条平滑的曲线,曲线在不同取值处的高度表示了该取值出
使用matplotlib画直方图和概率密度图
害,折腾了我好久 1. 直方图和概率密度图叠加 #python 画概率密度图#-*- coding: utf-8 -*-import matplotlib.pyplot as pltimport numpy as npimport seaborn as sns# 1)准备数据lengths = []with open("D:/length_analysis.tsv","r") as
非参数估计法之 parzen窗方法和k近邻方法估计概率密度
无论是参数估计还是费参数估计 其目的都是为了求出总体的概率密度函数 parzen窗 基本原理 嗯哼哼 ,画个圈圈 ,在圈圈里面又画一个正方形,在往圈圈里面随机扔豆豆,豆豆在正方形里面的概率约等于在正方形内的总数k比豆豆总数n即k/n,其正好是正方形与圈圈的面积比,假设正方形的面积为R 设豆豆落在正方形里面的概率为P = k/n,假设豆豆落在正方形的每一个点上的概率一样,则落在正方形中的任意
强化学习小笔记 —— 从 Normal 正态分布的对数概率密度到 tanh-Normal的对数概率密度
在学习 SAC 算法用于连续动作的代码时,遇到了一个不懂的地方,如下代码所示: # pytorchclass PolicyNetContinuous(torch.nn.Module):def __init__(self, state_dim, hidden_dim, action_dim, action_bound):super(PolicyNetContinuous, self).__ini
均匀分布二项分布泊松分布正态分布Z=X+Y的概率密度Z=X/YZ=XYmax{X,Y}的分布min{X,Y}的分布
泊松分布 均匀分布 正态分布 Z=X+Y Z=X/Y&&Z=XY max{X,Y}的分布&&min{X,Y}的分布
标量对矩阵求导、复合函数的概率密度
本总结是是个人为防止遗忘而作,不得转载和商用。 标量对矩阵求导 第二个等式的原因是 复合函数的概率密度 题目:给定X的概率密度fX(x),若Y = ax,a是某个正实数,求Y的概率密度。 遇到这样的问题时不是直接把y代入f(x)然后求,正确的做法是:
数学基础--概率密度
首先考虑这样一个问题,你点了一个外卖,外卖说会在两个小时送达。那么送达的时间如下图(本次问题不考虑你进行催单和其他特殊情况,请勿抬杠)。 ,若外卖在第30分钟到60分钟送达那么概率是多少呢?没错是(60-30)/120=1/4,我们是怎么判断的呢?我们通过面积判断 ,如下图:(⚠️注意第二张图与第一张图相比,只是我标明了纵坐标而已,其他并没有什么变化,而且其实我们知道纵坐标不影响目前我们求出概率
MATLAB | 对随机信号进行统计分析,绘制频次直方图、频率分布图,与理论概率密度进行比较
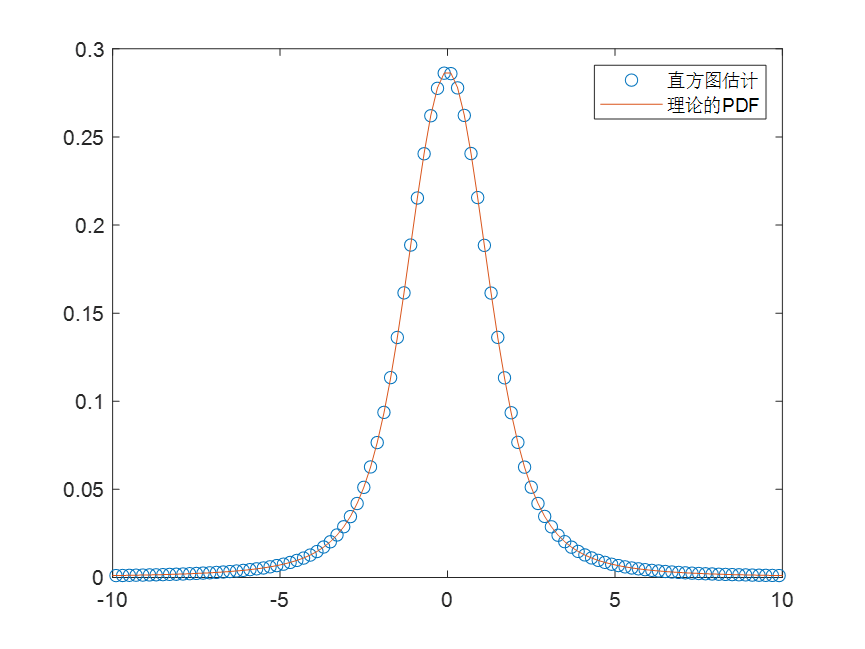
一、问题描述 对于一个随机信号,我们可以通过统计手段,得到其的频次分布图(直方图),并由此计算出它的频率分布图。当观察次数区域无穷大时,频率分布图近似于概率密度函数。 下面我们以稳定分布的随机变量为例,来对其进行分析,分析其频次直方图、频率分布图,并与理论概率密度进行比较。 二、解决思路 (1)生成随机变量。使用makedist()函数创建一个概率分布对象,在此基础上,使用random()函
线性回归模型笔记整理1 - 误差与分布(概率密度公式)
线性回归模型的参数求解 上篇9号博文已经解释过了。 1. 线性回归模型中的误差与分布 接下来,我们来看一下线性回归模型中的误差。正如我们之前所提及的,线性回归解释的变量(现实中存在的样本),是存在线性关系的。然而,这种关系并不是严格的函数映射关系,但是,我们构建的模型(方程)却是严格的函数映射关系的,因此,对于每个样本来说,我们拟合的结果会与真实值之间存在一定的误差,我们可以将误差表示为:
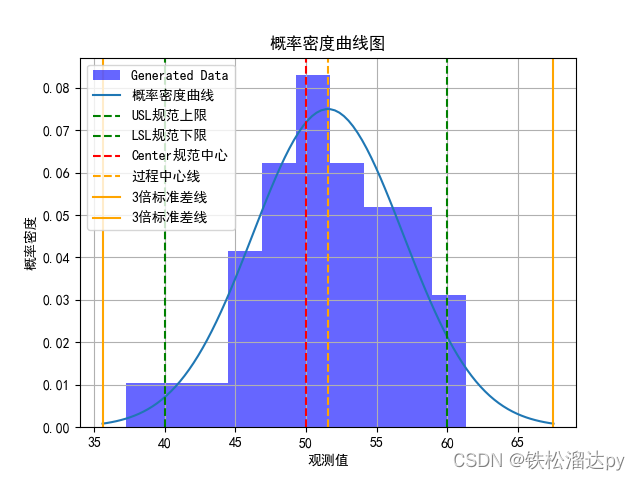
PYTHON计算CPK及规范限合格率,绘制直方图概率密度曲线
CPK(过程能力指数)是一个用于衡量一个过程的稳定性和一致性的统计指标,特别用于制造业和质量管理中。它衡量了一个过程的变异性与规范界限的关系,帮助确定过程是否能够产生合格的产品或服务。 正态分布假设:CPK的计算通常基于正态分布(或近似正态分布)的假设。这意味着过程数据应该呈现出类似正态分布的特征。如果数据不服从正态分布,可能需要进行转换或采用其他方法来处理。 CPK 的计算涉及以下步骤: