本文主要是介绍数学基础--概率密度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
首先考虑这样一个问题,你点了一个外卖,外卖说会在两个小时送达。那么送达的时间如下图(本次问题不考虑你进行催单和其他特殊情况,请勿抬杠)。
,若外卖在第30分钟到60分钟送达那么概率是多少呢?没错是(60-30)/120=1/4,我们是怎么判断的呢?我们通过面积判断 ,如下图:(⚠️注意第二张图与第一张图相比,只是我标明了纵坐标而已,其他并没有什么变化,而且其实我们知道纵坐标不影响目前我们求出概率,毕竟都是一样的纵坐标)。
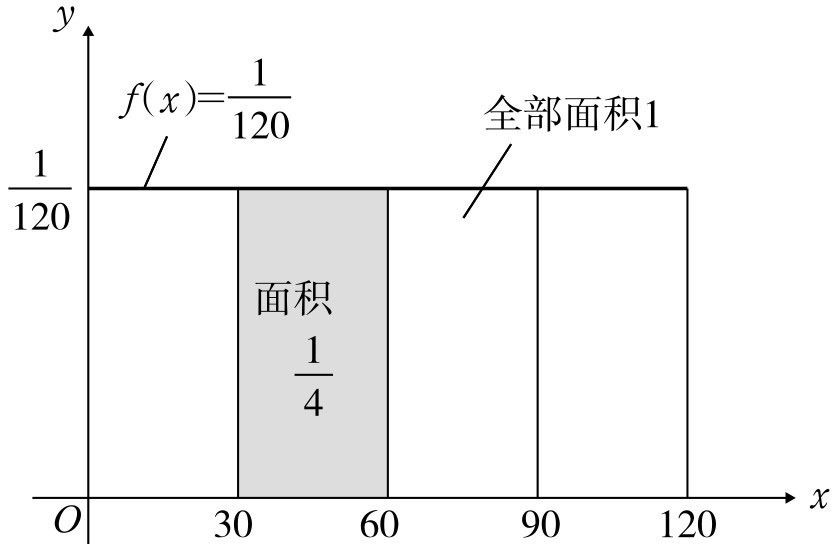
上述面积直接可以看出来,然后用阴影面积比上总面积就可以了。但是,如果面积是这样样子的呢?
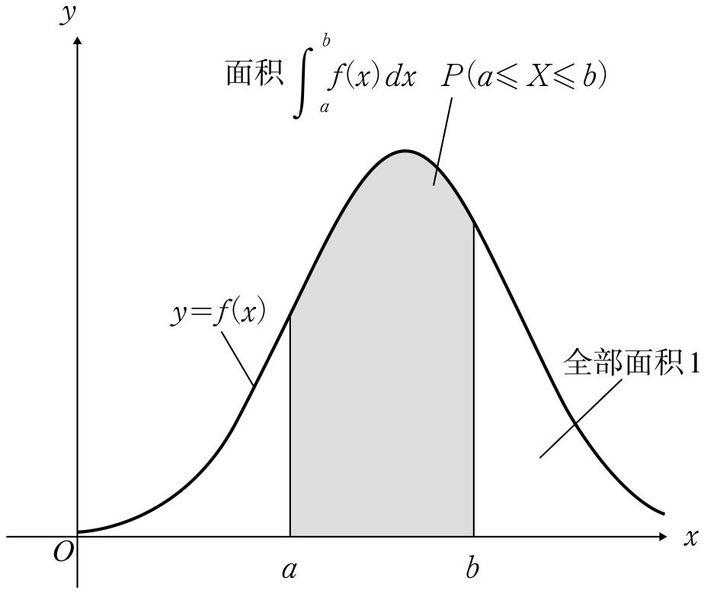
还是一样嘛,还是面积之比。没错!只不过这里我们想要求面积要用到积分来求,既然要积分,总得给我个函数吧,不然不是在欺负老实人吗。于是给你一个函数f(x),你去分别积分,就可以求出面积了,最后一比就是概率了。
大家注意到了吗?我的第二张图和第三张图的总面积都是1哦!,这就是玄妙所在。我们可以知道:第二张图的f(x)如下:
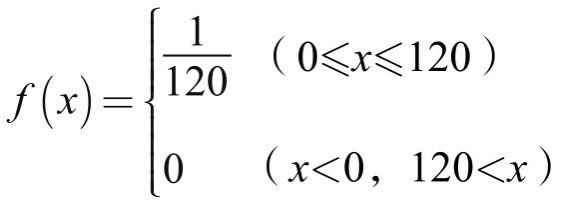
而第三张图的就是默认的f(x)。这里大家根据第二张图和第三张图计算可以得出两个结论:
1 f(x)总是≥0 ;
2 从负无穷到正无穷对f(x)积分面积始终为
1这里f(x)就是我们所说的概率密度函数,重点是⚠️我们一直所说的概率密度函数就是只我们想要求面积时候的那个图形的表达式。(牢记这句话你就不会在概率密度函数上犯迷糊)。
如果按照我们课本上面的直接上来就给你一个公式,如下:
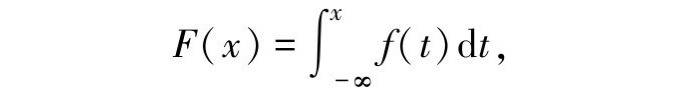
然后告诉你f(x)就是概率密度函数,我当时学习的时候也是很迷糊啊,凭什么就说f(x)是概率密度函数了,而且上来就是个积分(F(x)为分布范围)。
现在我们知道了:
- f(x)>=0是因为不管啥时候概率不能是负的吧
- f(x)从负无穷到正无穷的积分为什么一定要是1,因为我们要保、 证总的概率为1。通过这两个条件我们给出了概率密度函数的限定条件。
另外给出两个常见概率密度函数图像及其分布函数的图像:
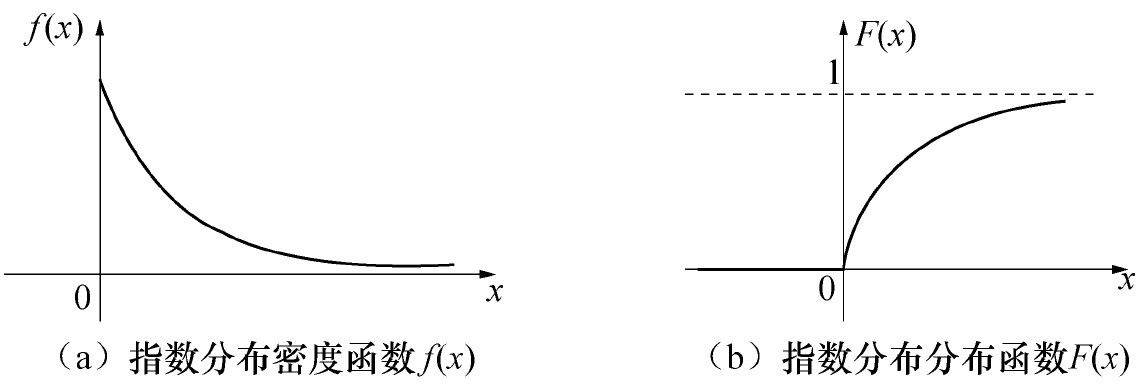
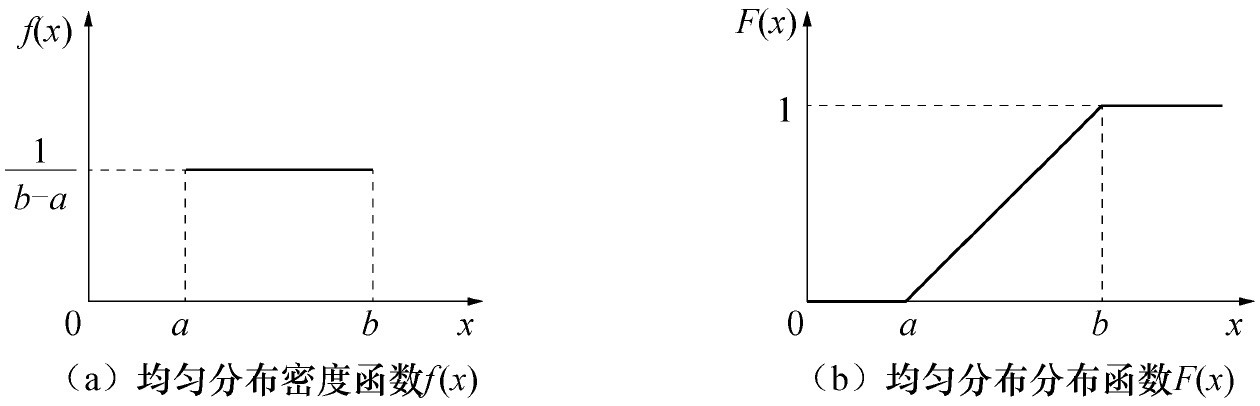
转载:https://www.zhihu.com/question/263467674
这篇关于数学基础--概率密度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







