最多水专题

LeetCode - 11 盛最多水的容器

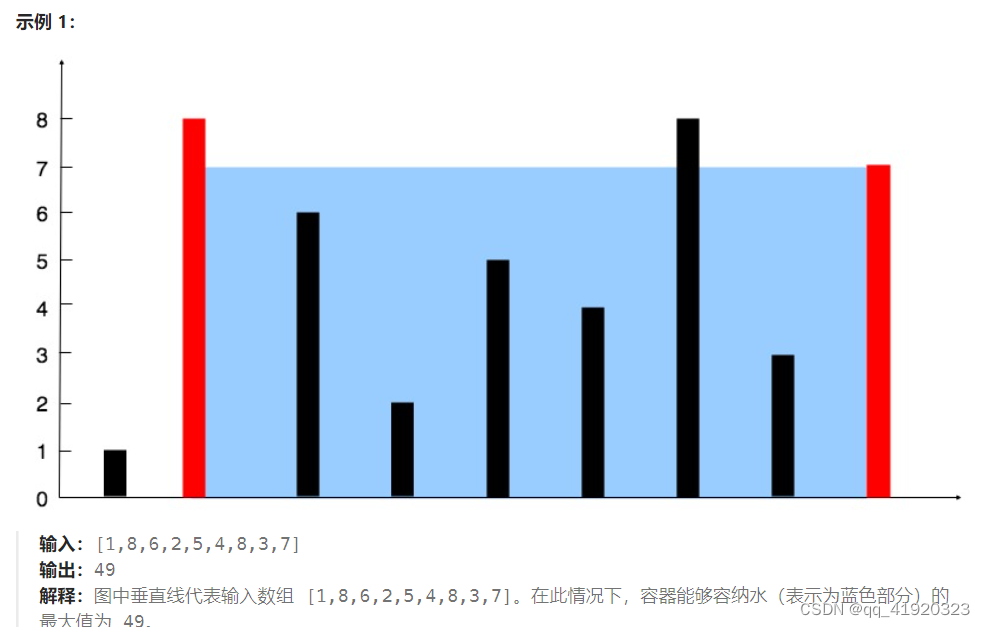
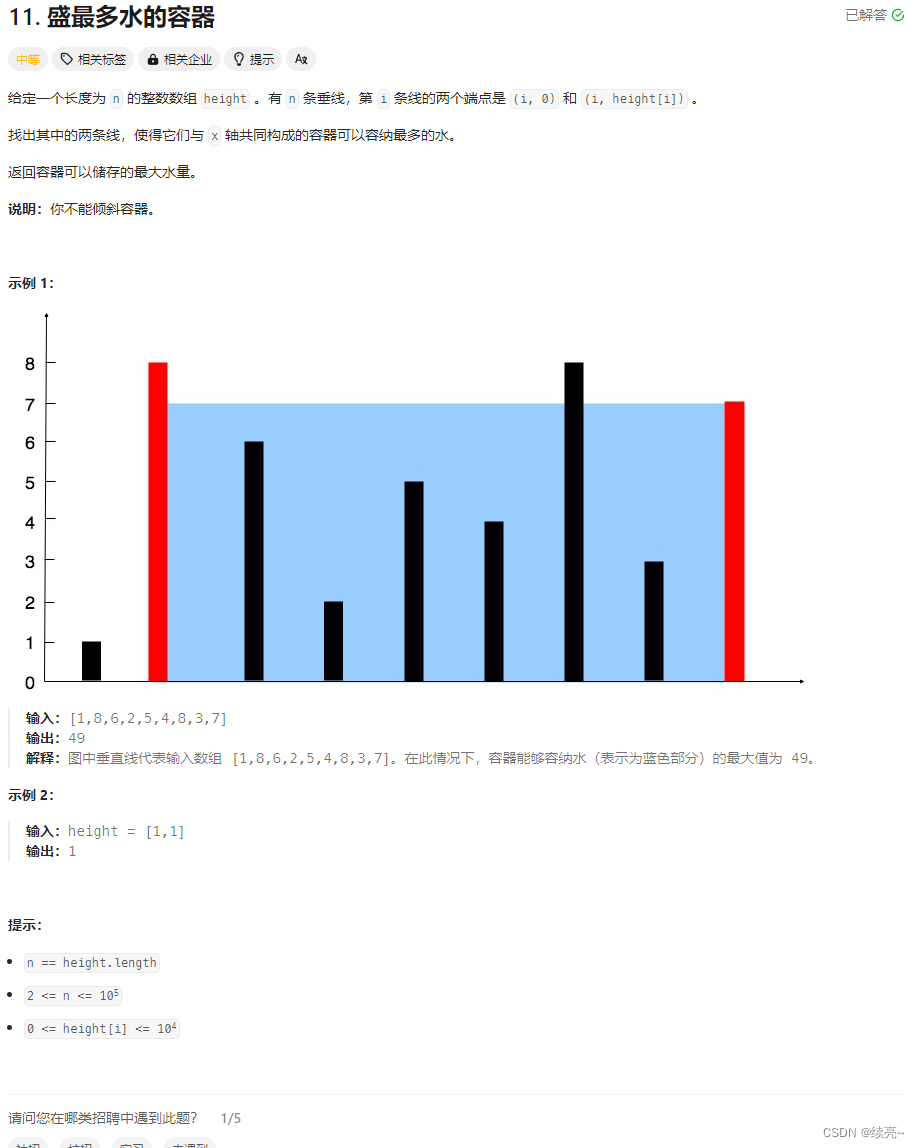
题目来源 11. 盛最多水的容器 - 力扣（LeetCode）题目描述给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明：你不能倾斜容器。示例1 输入：[1,8,6,2,

LeetCode11. 盛最多水的容器题解

LeetCode11. 盛最多水的容器题解题目链接： https://leetcode.cn/problems/container-with-most-water 示例思路暴力解法定住一个柱子不动，然后用其他柱子与其围住面积，取最大值。代码如下： public int maxArea1(int[] height) {int n = height.length;int

算法：11. 盛最多水的容器

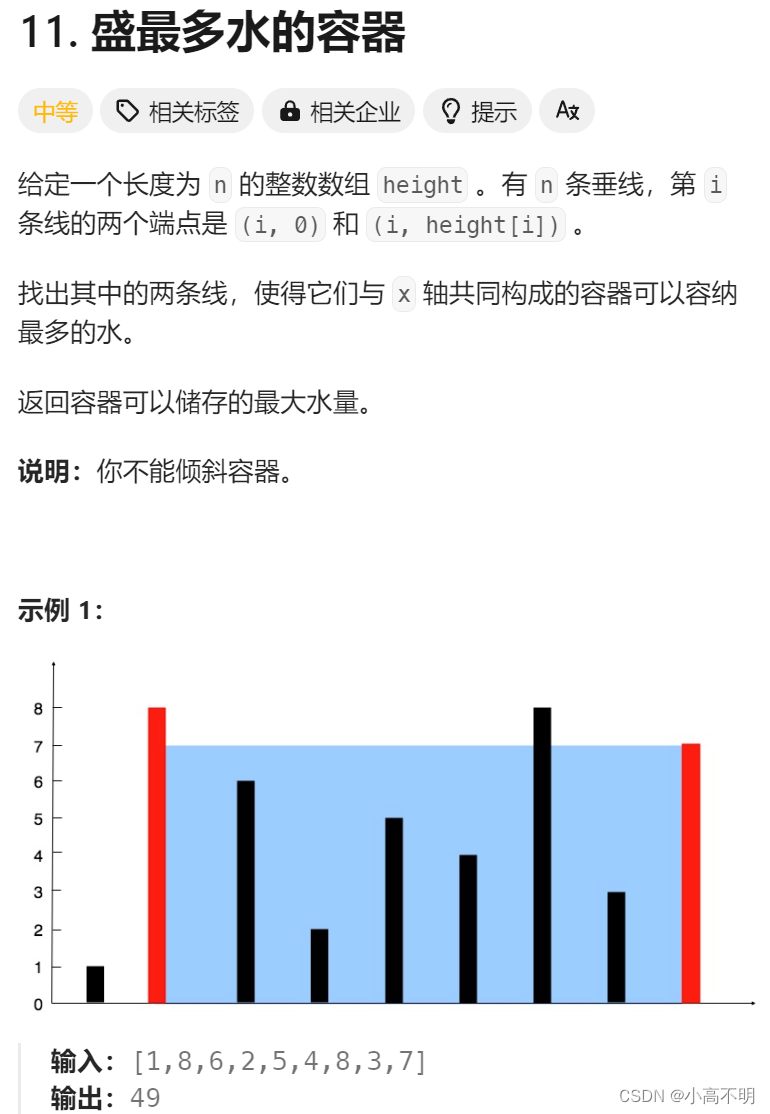
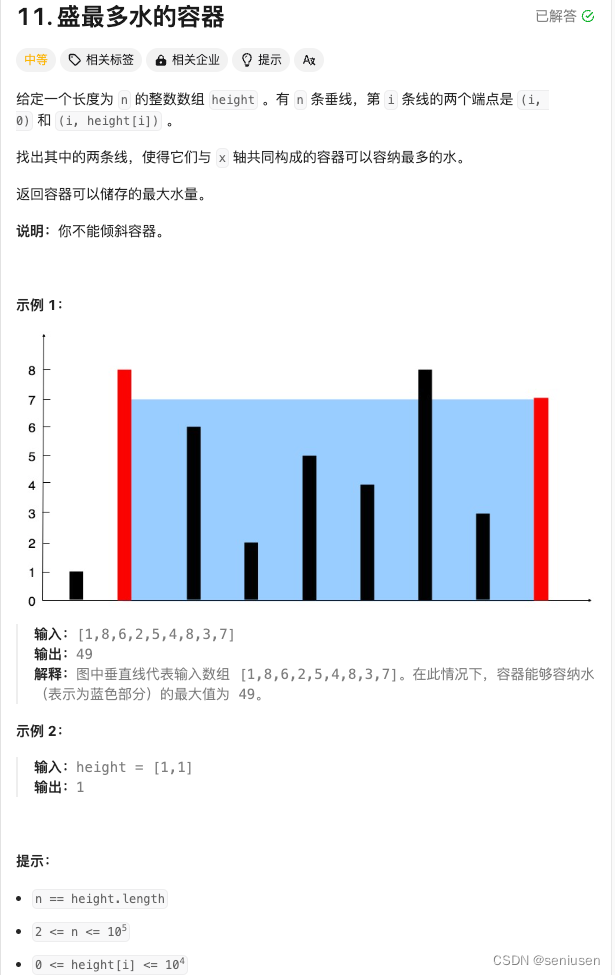
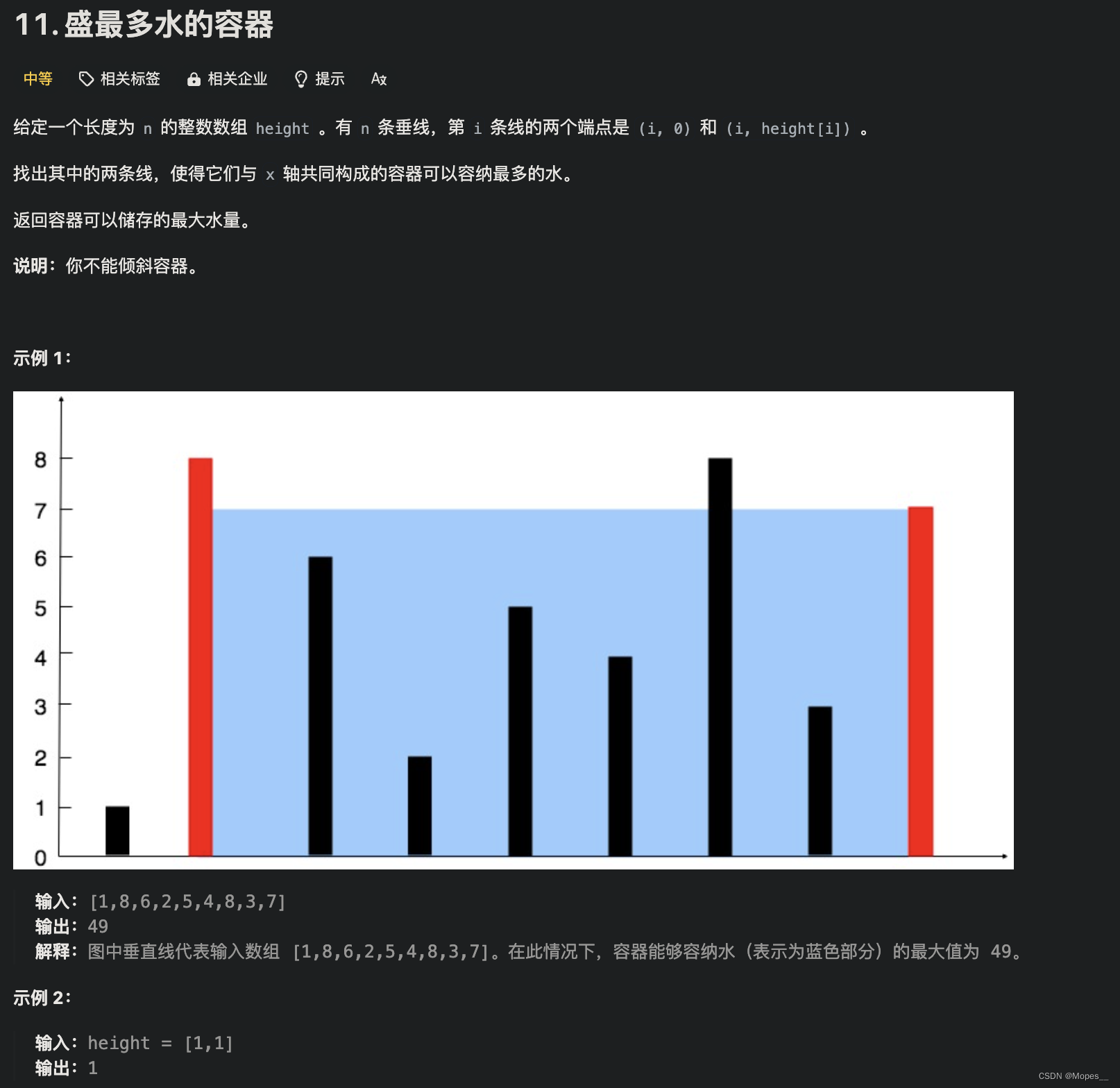
11. 盛最多水的容器给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明：你不能倾斜容器。示例 1：输入：[1,8,6,2,5,4,8,3,7]输出：49 解释：图中垂直

秋招突击——算法打卡——5/31——复习{采药问题、（状态压缩DP）小国王}——新做：{盛最多水的容器、整数转罗马数字}

文章目录复习背包模型——采药问题状态压缩DP——小国王思路分析实现代码参考新作盛最多的水个人实现思路分析实现代码参考分析思路分析实现思路整数转罗马数字个人实现思路分析实现代码参考实现思路分析实现代码总结复习背包模型——采药问题原题链接这里回忆的时候，还是有点问题，就是起点值怎么写？并不确定！然后关于这个表达式，也是弄了半天才想起来，还是要多多练习一下

LeetCode 算法：盛最多水的容器c++

原题链接🔗：盛最多水的容器难度：中等⭐️⭐️ 题目给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明：你不能倾斜容器。示例 1：输入：[1,8,6,2,5,4,8,3,7] 输出

[双指针] --- 快乐数盛最多水的容器

Welcome to 9ilk's Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏：算法Journey 本篇博客我们分享一下双指针算法中的快慢指针以及对撞双指针，下面我们开始今天的学习吧~ 🏠 快乐数 📒 题目解析题目链接：202. 快乐数 - 力扣（Le

LeetCode算法题：11. 盛最多水的容器（Java）（双指针问题总结）

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。提示： n == height.length2 <= n <= 10^50 <= height[i] <= 10^4 解题思路：定义两个指针

Leecode热题100---11：盛最多水的容器

题目：给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明：你不能倾斜容器。 C++：双指针解法要点：指针每一次移动，都意味着排除掉了一个柱子，每次移动有可能会增大面积的那条边。详细解释请参照：

leetcode-11. 盛最多水的容器(双指针)

11. 盛最多水的容器 /*** @param {number[]} height* @return {number}*/var maxArea = function (height) {// 时间复杂度 O(n)// 空间复杂度 O(1)let len = height.length;let left = 0,right = len - 1;let res = 0;while (left <

盛最多水的容器（双指针）

解题思路： 1，暴力解法（超时）我们可以使用两层for循环进行遍历。找到那个最大的面积即可，这里我就不写代码了，因为写了也是超时。 2，双指针法先定义两个指针一个在最左端，一个在最右端：矩形的体积是底*高，我们将两个指针之间的距离当做底，当两个指针移动时底一定会减小，所以如果此时高还在减小，那么他的面积肯定会减小，所以我们就找高增大的作为矩形的两边，因此就有了height[le

每日一题盛最多水的容器

. - 力扣（LeetCode）思路分析: 利用函数的单调性解决这道题两端取最小，最小的往里找就是高不变或者缩小宽减少一定是减小的因此这题可以使用左右指针实现 public int maxArea(int[] height) {int left = 0;int right = height.length - 1;int max = 0;int v = 0;while (lef

LeetCode：盛最多水的容器

盛最多水的容器给你n个非负整数a1，a2，…，an，每个数代表坐标中的一个点(i, ai) 。在坐标内画 n 条垂直线，垂直线i的两个端点分别为(i, ai) 和 (i, 0)。找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。说明：你不能倾斜容器。示例 1：输入：[1, 8, 6, 2, 5, 4, 8, 3, 7] 输出：49 解释：图中垂直线代表

LeetCode 11—— 盛最多水的容器

阅读目录 1. 题目2. 解题思路一3. 代码实现一4. 解题思路二5. 代码实现二 1. 题目 2. 解题思路一暴力法，遍历所有可能的垂线对 ( i , j ) (i, j) (i,j)，求取最大面积： a r e a = m i n ( h [ i ] , h [ j ] ) ∗ ( j − i ) area = min(h[i], h[j]) * (j -

盛最多水的容器——双指针

. - 力扣（LeetCode）双指针理解：以整体和局部的角度考虑：如果Left比Right矮，那么Left所有可能能组成的最大值此时就已经确定了，无论中间是否有比Right还要高的数；先记为Lmax 那么最终答案即为max(Lmax, Right与剩余的数的最优解) 继续分析如下图: 再去新的Left,与上一步的Right，以此类推.. 即可获取最终答案为什么

盛最多水的容器(双指针，短的向中间移)

这道题有些面善，大二的时候去参加字节跳动的笔试，有一道算法题就是这个，我当时可能写的是穷举我自己写的是穷举，时间复杂度是O(n^2) class Solution {public:int maxArea(vector<int>& height) {int max=0;int c;for(int i=0;i<height.size()-1;i++){for(int j=i+1;

用 PHP 来刷leetCode 之盛最多水的容器

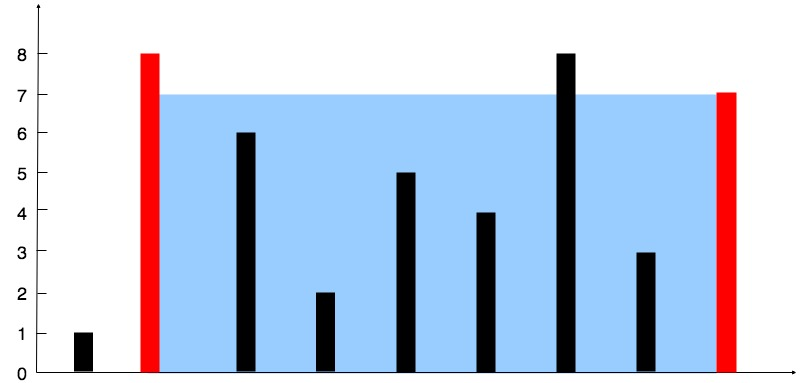
给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。说明：你不能倾斜容器，且 n 的值至少为 2。图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（

LeetCode - 11.盛最多水的容器

一. 题目链接 LeetCode - 11.盛最多水的容器二. 思路解释利用双指针的思想，定义一个left和reght，left指向首部，right指向尾部，计算当前两个指针所对应的高度构成容器的体积。根据当前双指针所指的高度的大小，然后让指针向内移动，直到left=right（一开始left指向首部，right指向尾部，此时容器的底是最大的，接下来随着指针向内移动，会

【C++】双指针算法：盛最多水的容器

1.题目 2.算法思路有两种方法：第一种：暴力穷举法，就是用两次循环将所有的可能性算出来，然后求出最大值。这种方法最容易想到，但时间复杂度是O(n^2)，一定会超时的！第二种：仔细观察题目特点，任意两条线之间的体积=短的那条线*两条线之间的距离。例如数组{2，3，8，1，7，6}。2和6之间的距离=2*5。根据体积的计算特点，对于2来说，它和其他数字之间的体

力扣11. 盛最多水的容器

题目描述：给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。说明：你不能倾斜容器，且 n 的值至少为 2。示例：输入：[1,8,6,2,5,4,8,3,7] 输出：49 题解：思路

力扣经典150题解析之二十八：盛最多水的容器

目录力扣经典150题解析之二十八：盛最多水的容器1. 介绍2. 问题描述3. 示例4. 解题思路5. 算法实现6. 复杂度分析7. 测试与验证测试用例设计测试结果分析 8. 总结9. 参考文献感谢阅读力扣经典150题解析之二十八：盛最多水的容器 1. 介绍在这篇文章中，我们将解析力扣经典150题中的第二十八题：盛最多水的容器。题目要求找出能够容纳最多水的容器，即找出数

leetcode 练习题 -- 11. 盛最多水的容器

题目描述：给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。说明：你不能倾斜容器，且 n 的值至少为 2。图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容

leetcode - 11 盛最多水的容器

题目大意给出一个非负整数数组 a1，a2，a3，…… an，每个整数标识一个竖立在坐标轴 x 位置的一堵高度为 ai 的墙，选择两堵墙，和 x 轴构成的容器可以容纳最多的水。解题思路这一题也是对撞指针的思路。首尾分别 2 个指针，每次移动以后都分别判断长宽的乘积是否最大。 class Solution{public:int maxArea(vector<int> &height

5、双指针-盛最多水的容器

解析：一个指针在数组的开始（我们称之为 L），另一个在数组的末尾（称之为 R）。然后，我们计算当前 L 和 R 之间的容器可以容纳的水的量，这个量由两个指针之间的距离（R - L）和两个指针指向的高度中较小的那个决定（因为水的高度不能超过两边中较低的那个）。每次迭代后，我们将较矮的那个指针向另一个指针的方向移动一步（因为如果移动较高的那个指针，容器的高度不会增加，而宽度会减少，所以容积只可

Python | Leetcode Python题解之第11题盛最多水的容器

题目：题解： class Solution:def maxArea(self, height: List[int]) -> int:l, r = 0, len(height) - 1ans = 0while l < r:area = min(height[l], height[r]) * (r - l)ans = max(ans, area)if height[l] <= height[

LeetCode十一题：容纳最多水的容器【11/1000 python】

👤作者介绍：10年大厂数据\经营分析经验，现任大厂数据部门负责人。会一些的技术：数据分析、算法、SQL、大数据相关、python 作者专栏每日更新： LeetCode解锁1000题: 打怪升级之旅 LeetCode解锁1000题: 打怪升级之旅https://blog.csdn.net/cciehl/category_12625714.htmlpython数据分析可视化：企业实战案例http

LeetCode-11. 盛最多水的容器【贪心数组双指针】

LeetCode-11. 盛最多水的容器【贪心数组双指针】题目描述：解题思路一：看提示知道是用贪心和双指针解法。贪心问题一般都比较难以想到。求面积肯定是希望底边(right - left)先越大越好，所以初始化left, right = 0, len(height) - 1。然后我们要求的是宽度w 乘以两个柱子中最短的柱子h，此时我们若移动比较高的柱子，结果只有两种：1.比最短的柱子