秋招突击——算法打卡——5/31——复习{采药问题、（状态压缩DP）小国王}——新做：{盛最多水的容器、整数转罗马数字}

本文主要是介绍秋招突击——算法打卡——5/31——复习{采药问题、（状态压缩DP）小国王}——新做：{盛最多水的容器、整数转罗马数字}，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

复习

背包模型——采药问题

• 原题链接
• 这里回忆的时候，还是有点问题，就是起点值怎么写？并不确定！
• 然后关于这个表达式，也是弄了半天才想起来，还是要多多练习一下！

#include <iostream>
#include <algorithm>using namespace std;
const int T = 1010;
const int M = 110;
int t[M],w[M];
int f[M][T];
int f1[T];
int n,m;int main(){cin>>n>>m;for (int i = 1; i <= m; ++i) {cin>>t[i]>>w[i];}// 遍历所有的药物// f[i][j]:表示在前i个物体下，容量为j的若干种装法中，最高的价值// 集合划分，对于第i个物体而言，也就是两种情况，装或者不装，装f[i-1][j - t[i]] + w[i],不装f[i-1][j]int res = 0;for (int i = 1; i <= m; ++i) {// 什么时候置零是一个问题，不知道怎么办f[i][0] = 0;for (int j = 1; j <= n && t[i] <= j; ++j) {f[i][j] = max(f[i-1][j],f[i -1][j - t[i]] + w[i]);res = max(res ,f[i][j]);}}cout<<res;// 使用滚动矩阵进行优化for (int i = 1; i <= m ; ++i) {for (int j = n; j >=  1 && t[i] <= j; j--) {f1[j] = max(f1[j],f1[j - t[i]] + w[i]);}}cout<<f[n]<< endl;
}

• 关于二维数组，基本思路是对的，就分两种情况，装或者不装，但是你得分开写
  参考信息
  

状态压缩DP——小国王

• 题目内容
  

思路分析

• 参考链接：状态压缩
• 这道题是真的不会，当时听了半天都没听懂，然后直接跳过了，但是也是dp的一种，经常考，还是要学习一下啊。
• 这里是使用二进制表示某一个行数的棋盘的状态

• 今天是不可能完全搞懂了，就搞懂局部吧，半个小时能懂多少懂多少，不然没时间搞别的东西了。再看一遍，也觉得是昏了头了，即使要是考了这个，直接跳过吧。

• 第i行的摆放位置，仅仅和第i-1行是有关系的，所以仅仅需要考虑第i-1的状态

• 第i行可以摆放x中状态，然后在判断一下是否和第i-1行是合法的，然后在进行累加，所以需要干两件事

  • 检查第i行的状态和第i-1行状态是否是合法的
  • 第i行有哪些合法状态
    暂时就分析到这里，明天就是看看代码还有怎么计算预设的状态转换了。
    

实现代码参考

#include <iostream>
#include <vector>using namespace std;typedef long long LL;const int N = 11, M = 1 << N, C = N * N;int n, m, K;
LL f[N][C][M];
int cnt[M];
vector<int> legal_state;
vector<int> state_trans[M];bool check(int state)
{return !(state & state >> 1);
}
int count(int state)
{int res = 0;for (int i = 0; i < n; ++ i) res += state >> i & 1;return res;
}
int main()
{cin >> n >> K;//预处理所有合法状态for (int st = 0; st < 1 << n; ++ st)//检查当前状态是否合法if (check(st))legal_state.push_back(st),cnt[st] = count(st);m = legal_state.size();//预处理所有合法状态的合法转移for (auto cur_st: legal_state)for (auto to_st: legal_state)if (!(cur_st & to_st) && check(cur_st | to_st))//上下不相邻且纵坐标也不相邻state_trans[cur_st].push_back(to_st);//动态规划f[0][0][0] = 1;for (int i = 1; i <= n; ++ i)for (int j = 0; j <= K; ++ j)for (auto &state: legal_state)for (auto &pre_st: state_trans[state])if (j - cnt[state] >= 0)f[i][j][state] += f[i - 1][j - cnt[state]][pre_st];//统计目标状态的所有方案数LL res = 0;for (auto state: legal_state) res += f[n][K][state];cout << res << endl;return 0;
}

作者：一只野生彩色铅笔
链接：https://www.acwing.com/solution/content/56348/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

新作

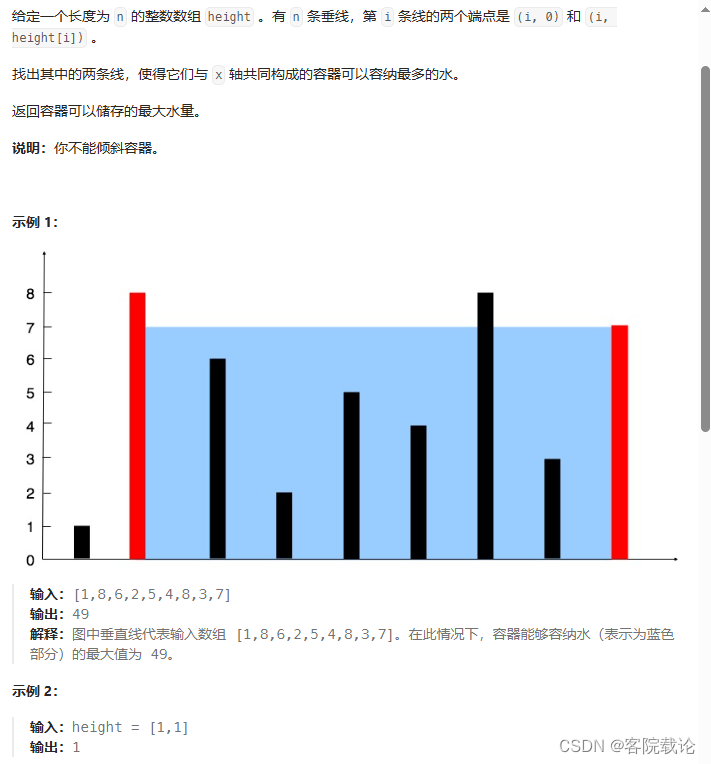
盛最多的水

题目链接

个人实现

思路分析

• 不像是动态规划，最直白的做法是进行暴力搜索的，但是问题空间的达到了10的10次方，有点爆炸，想想看怎么减少，但是就算去掉重复的，也是10的9次方。
• 对了，这个可以试试看双向指针，两边，哪边移动会变大，就移动哪边，移动之后，在计算一下体积有没有变大
• 双指针没想清楚，但是后来想清楚了，应该先找到最大值和次大值，然后分别向两边进行遍历，因为很显然，在最大值和次大值中间的数字，任何容积都是比这两个小的。所以只有可能向两边进行遍历。但是这里写的有点慢，就是求第二大的数字的时候，没写好，看看有什么更方便的方式。
• 这里有个问题
  • 并不知道怎么移动左右指标比较合理！！

实现代码

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;const int N = 100000;
int maxArea(vector<int>& h) {// 定义双指针int first = INT_MIN,second = INT_MIN,firstIdx,secondIdx;for (int i = 0; i < h.size(); ++i) {if (h[i] > first )   first = h[i] , firstIdx = i;if (h[i] > second && h[i] < first )   second = h[i] , secondIdx = i;}int l = min(firstIdx,secondIdx),r = max(firstIdx,secondIdx);int len ,vol = 0;while(l >= 0 || r < h.size()){len = r - l;int temp = min(h[l],h[r]) * len;vol = vol < temp ? temp:vol;// 然后根据情况进行迁移// 关于这里如何移动，并不知道怎么调整if (h[l] < h[l + 1])    l --;if (h[r] < h[r - 1])    r ++;}return vol;
}int main(){vector<int> n = {1,8,6,2,5,4,8,3,7};cout<<maxArea(n)<<endl;
}

参考分析

思路分析

• 好吧，我想多了，我这样做并不是最优的，是双指针，但是是从两边开始往中间移动的双指针，而且是两个指针进行比较，那个指针的数值比较低，然后移动哪一个？
• 证明过程比较形象，具体如下：
  • 用反证法，假设一个最优值，然后一边先到达最优值，然后在控制另外一边进行到达，然后反正在移动过程中不存在最优值

实现思路

int maxArea(vector<int>& h) {// 定义双指针int vol = 0,l = 0,r = h.size() - 1 ,len = 0;while(l < r){len = r - l;int temp = min(h[l],h[r]) * len;vol = vol < temp ? temp:vol;// 然后根据情况进行迁移// 关于这里如何移动，并不知道怎么调整if (h[l] < h[r])    l ++;else    r --; }return vol;
}

整数转罗马数字

• 题目链接：整数转罗马数字
  

个人实现

思路分析

• 数字并不是很大，所以直接进行遍历，逐个位数进行修改
• 直接暴力做

实现代码

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;const int N = 3999;
string intToRoman(int num) {// 不是4或者9开头，就减去最大值，并将该符号附加到结果，减去其值，将其与部分转换为罗马数字// 4或者9开头，使用减法形式// 只有10的次方可以连续出现三次，其他都不行// 将数字分成几个段落：// 1-3 ，可以使用最高位进行连续相加// 4：5-1// 6-8：5+1-3的组合// 9：10-1// 先处理1000，确定最高位int v = num / 1000,res = num % 1000;string s = "";if (v <= 3 && v >0)while(v)    s += "M" , v--;// 然后在获取百位v = res / 100,res %= 100;switch (v) {case 0:break;case 1:case 2:case 3:while(v){s += "C" , v--;}break;case 4:s += "CD";break;case 5:s += "D";break;case 6:s += "DC";break;case 7:s += "DCC";break;case 8:s += "DCCC";break;case 9:s += "CM";break;}// 然后在获取十位v = res / 10,res %= 10;switch (v) {case 0:break;case 1:case 2:case 3:while(v){s += "X" , v--;}break;case 4:s += "XL";break;case 5:s += "L";break;case 6:s += "LX";break;case 7:s += "LXX";break;case 8:s += "LXXX";break;case 9:s += "XC";break;}//然后在处理个位switch (res) {case 0:break;case 1:case 2:case 3:while(v){s += "I" , res--;}break;case 4:s += "IV";break;case 5:s += "V";break;case 6:s += "VI";break;case 7:s += "VII";break;case 8:s += "VIII";break;case 9:s += "IX";break;}return s;}
int main(){int n = 1;cout<<intToRoman(n)<<endl;
}

参考实现

思路分析

• 这是一道模拟的题目，也就是找规律的题目。规则有限，直接打表也行
  
• 但是这里是定义结果临界值，如果大于特定的值，就减去对应的值，

实现代码

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;const int N = 3999;
string intToRoman(int n) {string s = "";int num[] = {1,4,5,9,10,40,50,90,100,400,500,900,1000};string numRep[] = {"I","IV","V","IX","X","XL","L","XL","C","CD","D","CM","M"};for (int i = 12; i >=  0; i --) {while(n >= num[i]){s += numRep[i];n -= num[i];}}cout<<s<<endl;
}
int main(){int n = 1;cout<<intToRoman(n)<<endl;
}

总结

• 本来应该坚持一下，但是最近一直在忙论文，本来已经写好了，就差试验了，结果今天把实验做完了，发现实验效果差的不行，因该是方法不行，很难受，不过秋招在即，没什么时间了，就暂时放弃了。明天开始继续跟上了。毕竟论文已经投了，这是第二篇，就是没人给我看，我害怕自己毕不了业，中不了，所以才想写第二篇。不过现在看，每天抽点时间做实验吧，能成就成，不能成也没有办法。

这篇关于秋招突击——算法打卡——5/31——复习{采药问题、（状态压缩DP）小国王}——新做：{盛最多水的容器、整数转罗马数字}的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---