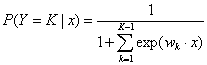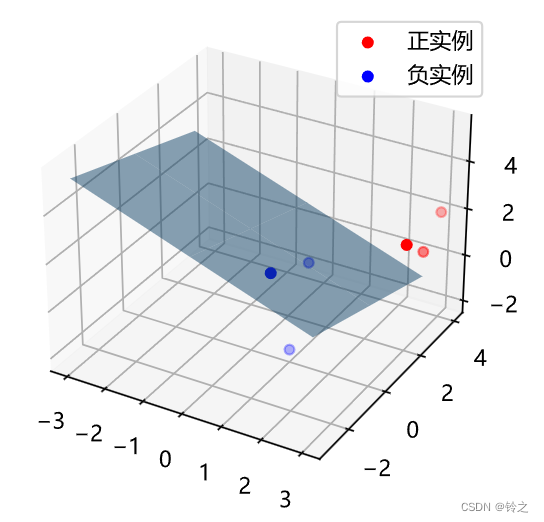
逻辑斯谛回归(LR)是经典的分类方法 1．逻辑斯谛回归模型是由以下条件概率分布表示的分类模型。逻辑斯谛回归模型可以用于二类或多类分类。 P ( Y = k ∣ x ) = exp ⁡ ( w k ⋅ x ) 1 + ∑ k = 1 K − 1 exp ⁡ ( w k ⋅ x ) , k = 1 , 2 , ⋯ , K − 1 P(Y=k | x)=\frac{\exp \left(w_{k}

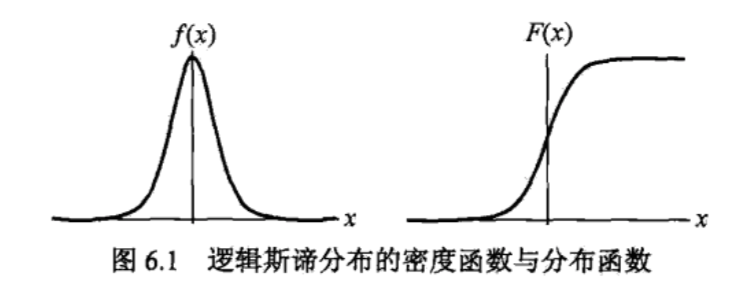
逻辑斯谛回归是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则，将其推广到分类问题得到最大熵模型。逻辑斯谛回归模型与最大熵模型都属于对数线性模型。 逻辑斯谛回归模型 逻辑斯谛分布：     设X是连续随机变量，X服从逻辑斯谛分布是指X具有下列的分布函数和密度函数：

目录 1 基本原理2 代码实现3 分岔图代码实现 1 基本原理 参考：维基百科 - 逻辑斯谛映射 逻辑斯谛映射（Logistic Map）是一种二次多项式的映射递推关系式，是一个由简单非线性方程式产生混沌现象的经典范例。其数学表达为： x n + 1 = μ x n ( 1 − x n ) x_{n+1}=\mu x_n(1-x_n) xn+1​=μxn​(1−x

逻辑回归模型 逻辑回归模型是一种分类模型，由条件概率分布P(Y|X) 表示，形式为参数化的逻辑分布，这里，随机变量X取值为实数，随机变量Y取值为1或0。 在学习逻辑回归时大家总是将线性回归作比较，线性回归模型的输出一般是连续的， 在线性回归模型中每一个输入x,都有一个对应的y输出。模型的定义域和值域都可以是[-∞, +∞]。但是逻辑回归输入可以是连续的[-∞, +∞],输出却一般是离散的

https://blog.csdn.net/huangjx36/article/details/78056375/

文章目录 6.2 最大熵模型6.2.1 最大熵原理6.2.3 最大熵模型的学习6.2.4 极大似然估计 《统计学习方法：李航》笔记 从原理到实现（基于python）-- 第3章 k邻近邻法 《统计学习方法：李航》笔记 从原理到实现（基于python）-- 第1章 统计学习方法概论 《统计学习方法：李航》笔记 从原理到实现（基于python）-- 第 2章感知机

文章目录 第6章 逻辑斯谛回归与最大熵模型6.1 逻辑斯谛回归模型6.1.1 逻辑斯谛分布6.1.2 二项逻辑斯谛回归模型6.1.3 模型参数估计6.1.4 多项逻辑斯谛回归 《统计学习方法：李航》笔记 从原理到实现（基于python）-- 第3章 k邻近邻法 《统计学习方法：李航》笔记 从原理到实现（基于python）-- 第1章 统计学习方法概论 《统计学习方法：

参考文献：机器学习与数据挖掘参考文献 一、二项逻辑斯谛回归模型 二项逻辑斯谛回归模型是如下的条件概率分布： 这里，x∈Rn是输入，Y∈{0,1}是输出，w∈Rn和b∈R是参数，w称为权值向量，b称为偏置，w·x为w和x的内积。有时为了方便，将权值向量和输入向量加以扩充，仍记作w，x，即w=(w(1),w(2),...,w(n),b)T，x=(x(1),x(2),...,x

文章目录 数据准备逻辑斯谛回归模型模型参数估计总结参考 数据准备 本文实现的是二项逻辑斯谛回归模型，因此使用的是处理过后的两类别数据 mnist_binary.csv，表中对原手写数据中0～4取作负类 -1，将5～9取作正类 +1。 另根据逻辑斯谛回归模型按条件概率分布定义： P ( Y = 1 ∣ x ) = e x p ( w ⋅ x ) 1 + e x p ( w

0. 概述： Logistic回归是统计学中的经典分类方法，最大熵是概率模型学习的一个准则，将其推广到分类问题得到最大熵模型，logistic回归模型与最大熵模型都是对数线性模型。 本文第一部分主要讲什么是logistic（逻辑斯谛）回归模型，以及模型的参数估计，使用的是极大对数似然估计以及梯度下降法，第二部分介绍什么是最大熵模型，首先介绍最大熵原理， 然后根据最大熵原理推出最大熵模型，