斯特林专题
近似求阶乘-斯特林公式
今天做Factstone Benchmark这个题，需要阶乘的近似值，用常规方法就是TLE，虽然我避开求阶乘，用为完成的中间值做为判断条件进而避免了TLE，但是这样的方法还是感觉不靠谱，经过查阅，果然有种可以近似求阶乘的东西，斯特林公式。 （baidu）斯特林公式（Stirling's approximation）是一条用来取n的阶乘的近似值的数学公式。一般来说，当n很大的时候，n阶乘的计算量十
组合数学 —— 斯特林数（Stirling）
【第一类斯特林数】 1.定理 第一类斯特林数 S1(n,m) 表示的是将 n 个不同元素构成 m 个圆排列的数目。 2.递推式 设人被标上1,2,.....p，则将这 p 个人排成 m 个圆有两种情况： 在一个圆圈里只有标号为 p 的人自己，排法有 S1(n-1,m-1) 个。p 至少和另一个人在一个圆圈里。 这些排法通过把 1,2....n-1 排成 m 个圆再把 n 放在 1,2.
Light OJ 1236 Race 第二类斯特林数
第二类斯特林数 n 匹马 分成1 2 3... n组 每一组就是相同排名 没有先后 然后组与组之间是有顺序的 在乘以组数的阶乘 #include <cstdio>#include <cstring>using namespace std;int dp[1010][1010];int a[1010];int main(){a[0] = 1;dp[0][0] = 1;for(int
![Hdu 3625 Examining the Rooms[第一类斯特林数]](/front/images/it_default2.jpg)
Hdu 3625 Examining the Rooms[第一类斯特林数]
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3625 题目意思： n(n <= 20)个房间。n把钥匙。每个房间有一把钥匙。一把钥匙只能开一把锁。 现在一个人手里没有钥匙，他可以强行打开一个门，然后拿出这个房间内的钥匙。不能够强行打开第一个门。。。 问最多强行打开k(k <= n)个房间的门的情况下，可以全部打开所有门的概率。。 分析
组合数学几类特殊的数，斯特林第一类数，斯特林第二类数，贝尔数
贝尔数 定义： Bn是基数为n的集合的划分方法的数目。集合S的一个划分是定义为S的两两不相交的非空子集的族，它们的并是S。例如B3 = 5因为3个元素的集合{a, b, c}有5种不同的划分方法： {{a}, {b}, {c}}, {{a}, {b, c}}, {{b}, {a, c}}, {{c}, {a, b}}, {{a, b, c}}。 B0是1，因为空集正好有1种划分方法
自然数幂和 拉格朗日插值法和第二类斯特林数法
写在这里，目的是在以后需要看的时候不用再去网上抄（划掉） 求 s ( n ) = ∑ i = 1 n i k 求s(n)=\sum_{i=1}^n i^k 求s(n)=i=1∑nik 拉格朗日插值法 给定若干个点值，(x0,y0)，(x1,y1)，(xn,yn)，它们的差值多项式 L ( x ) = ∑ i = 0 n y i ∗ ∏ j ≠ i x − x j x i − x j L(
POJ 1430 Binary Stirling Numbers （斯特林数）
题意:给你n,k,求S(n,k) mod 2。 题解：没什么好说的，知道公式就好解决。C(z,w) = z! / [(w!) * (z-w)!]，要判断奇偶性只需要统计一下分子分母的所含的因子2的个数。 #include<cstdio>#define lint __int64lint getTwo ( lint x ){lint cnt = 0, bit = 2;wh
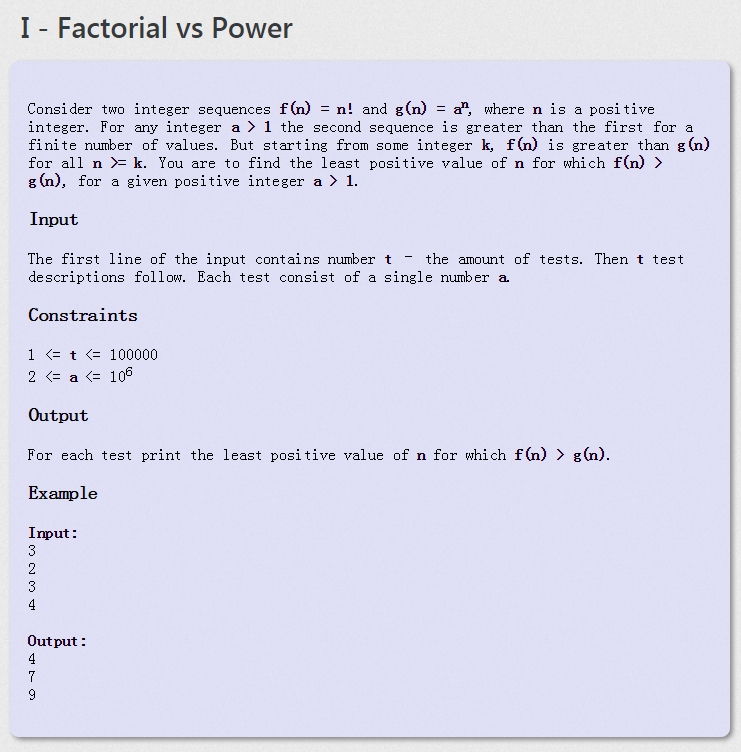
ACM 斯特林公式 Factorial vs Power
斯特林公式（Stirling's approximation）是一条用来取n的阶乘的近似值的数学公式。一般来说，当n很大的时候，n阶乘的计算量十分大，所以斯特林公式十分好用，而且，即使在n很小的时候，斯特林公式的取值已经十分准确。 SPOJ Factorial vs Power 题目大意：对于给定的a，求满足的 n! > an 最小的n。 思路：利用斯特林公式，可以代替到n！
罗马诺：斯特林专注于切尔西，并没有接触过利雅得新月
足球直播网-足球直播在线直播观看免费直播吧足球直播网是一个专业足球直播在线观看免费直播平台，专业提欧洲杯直播,足球直播在线直播观看免费直播吧中文jrs无插件直播，五大联赛直播，英超，德甲，法甲，意甲，西甲，及中超，中甲等最新足球直播内容。https://www.babycare.org.cn 2月28日讯 据媒体报道，沙特球队打算引进斯特林，但球员们将拒绝对方的巨额报价。据著名转会记者罗马诺
![[数位dp][斯特林反演] Jzoj P5765 相互再归的鹅妈妈](https://img-blog.csdnimg.cn/2022010621163057348.png)
[数位dp][斯特林反演] Jzoj P5765 相互再归的鹅妈妈
Description Input Output Sample Input Input 13 1101Input 24 310Input 35 1001 Sample Output Output 11Output 21978Output 3598192244 Data Constraint 对于所有数据，保证
jzoj5765 【省选模拟8.5】相互再归的鹅妈妈 （集合划分，斯特林反演）
mk<=5e6，m<=5e4 m k <= 5 e 6 ， m <= 5 e 4 mk<=5e6，m<=5e4 解法 先考虑可以有相同怎么做： 枚举一个第一个脱离限制的位置，然后用一个脱离限制的数来安排使得异或和为0，其他数可以任意取（要分是否脱离限制确定方案数）。这样可以计算出g(n)表示n个可以相同的数，异或和为0的答案。 斯特林反演式子： [n=1]=∑m的集合划分A
hdu2512 第二类斯特林数
题意： 给出n个卡，求这些卡放在一个包里面的方法数 + 放在两个包的方法数 + 放在三个包的方法数 。。。。放在n个包的方法数 的总和 题解： 模板题 第二类斯特拉数 将p个物体排成k个非空集合排列的方法数。s(p,0)=0 ,p>=1 ;s(p,p)=1 ,p>=0。 递推式：s(p,k)=k*s(p-1,k)+s(p-1,k-1) ,1<=k<=p-1
《洛谷深入浅出》斯特林数
斯特林数被分为三种，但我们这只介绍两种。即第一类斯特林数，和第二类斯特拉数。 第一类斯特林数指的是： 将n个不同元素，变成m个圆排列的方案数量。第一类斯特林数，分为有符号和无符号。通常我们只研究无符号斯特林数： 1，递推求第一类斯特林数： 我们用dp的思路来研究第n个元素，对于第n个元素而言，要变成m个圆排列，有两种情况。 第一种：第n个元素自己成为一个圆排列，那么也就是前n-1
![[LuoguP1829]Crash的文明表格(二次扫描与换根+第二类斯特林数)](https://i.loli.net/2019/08/31/N6DbcXtPal7yQrB.png)
[LuoguP1829]Crash的文明表格(二次扫描与换根+第二类斯特林数)
Solution: 由于\[ x^m = \sum_{i=0}^m{~m~\choose i}{~x~\brace i}i! \] 将所求的式子化成这样，挖掘其性质，考虑是否能从儿子转移(或利用以求得信息)。\[ \begin{aligned} S(u) &= \sum_{i=1}^ndis(u,i)^k\\ &= \sum_{i=1}^n\sum_{j=0}^k{dis(u, i)
第一类第二类斯特林数学习笔记
第一类斯特林数 p p p个不同人围着 k k k个不同圆桌坐，要求每桌非空，方案数即为 S ( p , k ) S(p,k) S(p,k) 递推 边界 S ( p , p ) = 1 ( p > = 0 ) , S ( p , 0 ) = 0 ( p > = 1 ) S(p,p)=1(p>=0),S(p,0)=0(p>=1) S(p,p)=1(p>=0),S(p,0)=0(p>=1)