[数位dp][斯特林反演] Jzoj P5765 相互再归的鹅妈妈

Description

Input

Output

Sample Input

Input 1
3 1
101
Input 2
4 3
10
Input 3
5 100
1

Sample Output

Output 1
1
Output 2
1978
Output 3
598192244

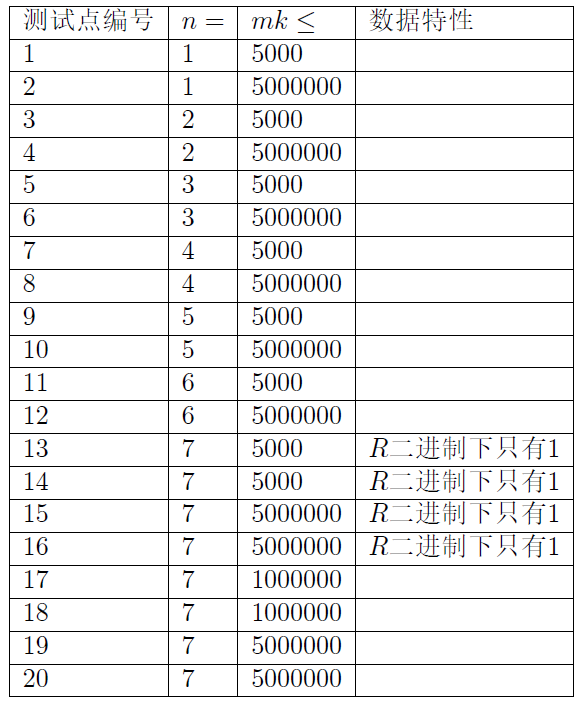
Data Constraint

对于所有数据，保证满足m<=50000

 

 

题解

• 题目大意：选出n个0~R-1的数，两两不能相同，要使得这n个数的异或和为0，求方案数
• 要求求无序方案，可以转化为求有序方案，最后除n!
• 现在，考虑一下，如果不要求两两不能相同（就是可以相同），可以怎么做
• 枚举脱离限制的位置（该位置在R中必须为1），脱离限制也就是说后面怎样选都不会超过R（也就是R为1的位置选了0）
• 可以用g(n)表示，选n个数异或值为0的方案数
• 然后，考虑加上两两必须不同
• 可以用斯特林反演式子来求容斥
• 式子：[?=1]=∑︀∏︀(?,?=1)(?[?] − 1)!(−1)^?[?]−1
  
• 枚举一个m的集合划分，其实k就是这种集合划分方案的几何数，而a表示各个集合的大小（可以用dfs实现）
• 注意，答案最后要除于n!，要用逆元做

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define M 5000010
#define N 8
#define ll long long
#define up(x,y) x=(x+(y))%mod
using namespace std;
const int mod=1000000007;
int n,m,K,w[M],p2[M][N],pw[M][N];
ll g[N],C[N][N],f[N],fac[N],ans;
char s[50010];
bool a[M];
ll ksm(ll a,ll b)
{
    ll r=1;
    for(;b;b>>=1,a=a*a%mod) if(b&1) r=r*a%mod;
    return r;   
}
void find(int num,int v)
{
    if(v>n)
    {
        ll c=1,cnt=0;
        for(int i=1;i<=num;i++) c=c*fac[f[i]-1]*((f[i]&1)?1:-1)%mod;
        for(int i=1;i<=num;i++) if(f[i]&1) cnt++; else c=c*w[1]%mod;
        up(ans,c*g[cnt]);   
        return;
    }
    for(int i=1;i<=num+1;i++) f[i]++,find(max(num,i),v+1),f[i]--;
}
int main()
{
    scanf("%d%d%s",&n,&K,s+1);
    m=strlen(s+1);
    for(int i=0;i<K;i++)
        for(int j=1;j<=m;j++)
            a[i*m+j]=s[j]-'0';
    m*=K;
    for(int i=m,mi=1;i;i--,mi=(mi<<1)%mod) w[i]=(w[i+1]+mi*a[i])%mod;
    fac[0]=1;
    for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;  
    C[0][0]=1;
    for(int i=1;i<=n;C[i][0]=1,i++)
        for(int j=1;j<=i;j++)
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
    bool flag=0;
    g[0]=1;
    for(int i=0,tmp=1;i<=m+1;i++,tmp=(tmp<<1)%mod)
    {
        p2[i][0]=pw[i][0]=1;
        for(int j=1;j<=n;j++) p2[i][j]=(ll)tmp*p2[i][j-1]%mod,pw[i][j]=(ll)w[i]*pw[i][j-1]%mod;
    }
    for(int i=1;i<=m;flag|=a[i],i++)
        if(a[i])
        for(int j=1;j<=n;j++)
            if(!flag||!(j&1))
                for(int k=0;k<=((j-1)>>1);k++)
                    up(g[j],C[j][k<<1]*pw[i+1][k<<1]%mod*p2[m-i][j-(k<<1)-1]);
    find(0,1);
    printf("%lld",(ans+mod)*ksm(fac[n],mod-2)%mod);
    return 0;
}