开方专题
0x5f3759df这个快速开方中的常数的数学依据和原理
Quake-III Arena (雷神之锤3)是90年代的经典游戏之一。 该系列的游戏不但画面和内容不错,而且即使计算机配置低,也能极其流畅地运行。这要归功于它3D引擎的开发者约翰-卡马克(John Carmack)。事实上早在90年代初DOS时代,只要能在PC上搞个小动画都能让人惊叹一番的时候,John Carmack就推出了石破天惊的Castle Wolfstein, 然
求一个正整数N的开方,要求不能用库函数sqrt(),结果的精度在0.001
#include<iostream> using namespace std; int main() { int N; cout<<"输入N的值:"; cin>>N double x1 = 1;//初值 double x2 = x1/2.0+N/2.0; while( fabs(x2-x1)>0.001)
花神游历各国(洛谷:线段树区间开方)
主要还是注意到两个点,一个是区间最大值为小于等于1的时候再怎么开方都是1所以不用修改,第二个点事数据范围是1e12,开方六次区间最大值就会变为1,当一个区间修改超过六次就返回. using i64 = long long;using ll = long long;constexpr ll inf = 1e18;struct Info {ll sum = 0;ll max = -inf;vo
NEFU 1317 神奇的开方运算(线段树)
神奇的开方运算 Problem:1317 Time Limit:1000ms Memory Limit:65535K Description 给出一个数组,现有两种操作1.将某一个区间所有数开方(向下取整)2.询问某一个区间的区间和 Input 多组样例,对于每组样例第一行输入一个数 N(1<=N<=1e5)
【力扣100】279.完全平方数 || python中开方表示i**(0.5)
添加链接描述 思路: 先设置全是1的可能dp数组;dp[i]表示数值为i的数的可以由最少平方数构成的个数遍历dp数组,现在数值来到i,那么枚举j,j的范围是[1,开方(i)+1)(左开右闭),因为开方会int全部取整数部分;我们发现,现在问题变成了dp[i-j*j]最少平方数的个数上,这就是动态规划 class Solution:def numSquares(self, n: int) ->
Quake-III代码里神奇的浮点开方函数
Quake-III Arena (雷神之锤3)是90年代的经典游戏之一。该系列的游戏不但画面和内容不错,而且即使计算机配置低,也能极其流畅地运行。这要归功于它3D引擎的开发者约翰-卡马克(John Carmack)。事实上早在90年代初DOS时代,只要能在PC上搞个小动画都能让人惊叹一番的时候,John Carmack就推出了石破天惊的Castle Wolfstein, 然后再接再励,doom,
Java大数开方模板及判断一个大数是否是平方数模板
判断是否是平方数 public static int judge (BigInteger x)///通过二分在区间(0,x)寻找是否有平方等于n的数{BigInteger left=BigInteger.ZERO,right=x,mid,ans;int sign;while(left.compareTo(right)<=0)///l<=r 注意有带等号{mid=left.add(right).
【面试题LeetCode69】求一个正数的开方
面试中遇到的是:给一个正数,包括浮点数,求它的开方,精度为0.01,二分查找的思路。 实现代码: public class Sqrt {public static void main(String[] args) {int num = 2147395599;System.out.println(sqrt(num));}private static int sqrt(int num) {if
实对称正定矩阵的开方
有前辈给出了【实对称正定矩阵存在平方根的证明】,证明过程点击此处。 任何一个实对称正定矩阵都可以表示成一个实对称正定矩阵的平方. 假设 A A A 为实对称正定矩阵,则存在实对称正定矩阵 B B B 使 A = B 2 = B ∗ B = B H B A=B^2=B*B=B^{H}B A=B2=B∗B=BHB 即 A 1 / 2 = B A^{1/2}=B A1/2=B
如何计算置信区间,RMSE均方根误差/标准误差:误差平方和的平均数开方
如何通过部分样本来计算总体的一个置信区间呢?主要有下面几个步骤: step1:首先明确要求解的问题。就是你要预估什么?不管是全校学生身高还是学生成绩。 step2:求抽样样本的平均值与标准误差(standard error,RMSE,均方根误差)。注意标准误差与标准差(standard deviation)不一样(标准差反映了整个样本对样本平均数的离散程度,标准误差反映样本平均数对总体平均
chatgpt赋能python:Python里的开方符号:介绍和用法
Python里的开方符号:介绍和用法 如果你是一个Python编程工程师,你肯定知道许多数学操作与函数在Python类库中都有相应的实现。其中一个特别的功能就是计算平方根和其他次方根,这是由Python内置的math模块提供的。这篇文章将重点介绍Python中的开方符号和如何在Python中使用它。 什么是开方 开方就是一个数的n次方等于另一个数a,那么我们称a的开n次方为这个数。例如,2的
【线段数】[LUOGU 上帝造题的七分钟2 / 花神游历各国] 线段树/分块 区间开方
题目: 题目链接:[LUOGU 上帝造题的七分钟2 / 花神游历各国] 题解: 这个题其实在之前我写的数列分块中的有一道题很一样,几乎一模一样了,也是让区间开方,分块写就很好理解,然后现在用线段树写其实大体上的解是一样的但是呢,就是套路不是很一样,,, 这个题重要的就是在一点,对于要好多次开方的数,你会发现,一个在1e12之内的数你对它开最多开方(下取整)六次即可开到1,或者是0,这样的话如果
编写python程序计算下面各表达式的值 根号派2+3,[宜配屋]听图阁 - Python计算开方、立方、圆周率,精确到小数点后任意位的方法...
Python计算的位数 在电脑上做了一个实验,看看python能计算到多少位,一下是结果。 x = math.sqrt((3)) print ("%.53f"%(x)) print ("%.63f"%(x)) print ("%.83f"%(x)) 1.73205080756887719317660412343684583902359008789062500 1.7320508075688771
python怎么复数乘方开方_初中一年级数学跟不上应该怎么办呢?
2020-10-20 16:59:17文/董玉莹 为什么学生到了初中,数学就突然跟不上了,怎么办? 初一数学学习方法 1、做好预习 单元预习时粗读,了解近阶段的学习内容,课时预习时细读,注重知识的形成过程,对难以理解的概念、公式和法则等要做好记录,以便带着问题听课。 2、认真听课 听课应包括听、思、记三个方面。听,听知识形成的来龙去脉,听重点和难点,听例题的解法和要求。思,一是要善于联想、




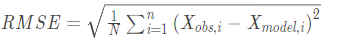

![【线段数】[LUOGU 上帝造题的七分钟2 / 花神游历各国] 线段树/分块 区间开方](https://img-blog.csdnimg.cn/20190902165350208.png)
![编写python程序计算下面各表达式的值 根号派2+3,[宜配屋]听图阁 - Python计算开方、立方、圆周率,精确到小数点后任意位的方法...](https://img-blog.csdnimg.cn/img_convert/783bc90990f846659eddfcbd0692f8ee.png)
