因子分析专题
通过因子分析识别消费者偏好的潜在因素的案例
因子分析是一种统计方法，用于研究变量之间的潜在关系。它是一种降维技术，通过识别较少数量的因子（或称为维度、成分）来解释多个观测变量之间的相关性。这些因子是不可观测的潜在变量，它们被认为是原始变量的潜在原因。 因子分析的主要步骤包括： 数据收集：收集相关变量的数据，这些变量之间可能存在某种程度的相关性。 数据标准化：由于原始数据可能具有不同的量纲和数值范围，通常需要对数据进行标准化处理。
综合评价 | 基于因子分析和聚类分析的节点重要度综合评价（Matlab）
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 综合评价 | 基于因子分析和聚类分析的节点重要度综合评价（Matlab） 程序设计 完整程序和数据获取方式：私信博主回复基于因子分析和聚类分析的节点重要度综合评价（Matlab）。 参考资料 [1] http://t.csdn.cn/pCWSp [2] https://download.
文本挖掘之降维技术之特征提取之因子分析（FA）
因子分析法（FA） 因子分析法是通过将原有变量内部的相互依赖关系进行数据化，把大量复杂关系归为少量的几个综合因子的统计方法。它的基本思想是通过分析各变量之间的方差贡献效果，将大的即相关性高的联系比较紧密的分在同一个类别中，而不同类的则相关性是比较低的，这其中一个类别描述了一种独立结构，这个结构在因子分析法中叫做公共因子。这个方法的研究目的就是尝试使用少数几个不可测的通过协方差矩阵计算得来
当 Alphalens 遇上 DolphinDB：单因子分析利器再升级
多因子投研一直都是量化投资领域当中的重要基石，Alphalens 和 DolphinDB，作为知名的单因子分析框架和基于高性能时序数据库的时序计算平台，无疑是备受瞩目的两大因子投研利器。当二者相结合，将碰撞出怎样令人期待的火花？ 1. Alphalens 和 DolphinDB 的简介 Alphalens 是 Quantopian 用 Python 开发的一个因子分析（评价）工具包。我们用 D
MATLAB算法实战应用案例精讲-【数模应用】因子分析（附MATLAB和python代码实现）
目录 前言 算法原理 SPSS因子分析 操作步骤 结果分析 SPSSAU 因子分析案例 1、背景 2、理论 3、操作 4、SPSSAU输出结果 5、文字分析 6、剖析 疑难解惑 同源方差或共同方法变异偏差，Harman单因子检验？ 提示出现奇异矩阵？ 因子得分和综合得分？ 因子分析计算权重？ KMO值过低？ 无论如何均‘张冠李戴’或‘纠缠不清’？ 因子分析
MATLAB基础应用精讲-【数模应用】验证性因子分析（CFA）（最终篇）（附python和R语言代码实现）
目录 算法原理 1.因子分析 1.1 探索性因子分析 1.2 验证性因子分析
利用聚宽JQFactor进行单因子分析的基本概念和分析结果详解
JQFactor是聚宽提供的单因子分析Python包，限定在聚宽的研究环境中使用。另外聚宽还提供了一个可以在本地Python开发环境中使用的jqfactor_analyzer，在本地直接用pip安装即可。二者大同小异。这里以JQFactor为例介绍其单因子分析的基本概念和分析结果的详细说明。 这是本文用到的示范代码:https://download.csdn.net/download/u0103
主成分分析和因子分析及其在R中的…
1 主成分分析和因子分析比较 主成分分析和探索性因子分析是两种用来探索和简化多变量复杂关系的常用方法，它们之间有联系也有区别。 主成分分析（PCA）是一种数据降维方法，它能将大量相关变量转化为一组很少的不相关变量，这些无关变量称为主成分。例如，使用PCA可将30个相关（很可能冗余）的环境变量转化为5个无关的成分变量，并且尽可能地保留原始数据集的信息。 相对而言，探索性因子分析（EFA）是
![[SPSS]因子分析和因子得分的SPSS实现——学生成绩因子构成和分科建议实例](https://img-blog.csdnimg.cn/2018121211272012.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1RPTU9DQVQ=,size_16,color_FFFFFF,t_70)
[SPSS]因子分析和因子得分的SPSS实现——学生成绩因子构成和分科建议实例
学生成绩因子构成和分科建议 数据概况： 因子分析： 将除序号外的变量都移入变量框中： 打开“描述”选项卡，勾选原始分析结果，这个结果会给出各因子的特征值、各因子特征值占总方差的百分比以及累计百分比。 选中“抽取”选项卡，方法选择主成分法；因子分析输出选择未旋转的因子解，输出因子载荷矩阵；因子抽取原则是基于特征值大于1的因子。 点击“旋转”选项卡，选择“最大方差
单因子分析 —— 异常换手率因子
1、单因子分析概述 主要步骤： 1、每个月底，按单因子值将股票池中的可用股票分5组。 2、每组按每天的流通市值，和股票的每日 close-to-close 收益率，计算每天的每组加权收益。 3、以上循环至时间结束，得到每组的累计收益率等相关数据。对其进行分析。 4、分组时去掉ST、停牌、上市时间不到半年的股票。 5、不考虑交易成本和损耗。 6、数据从本地数据库中获取。 2、因子选择与预处理
因子分析（SPSS和Python）
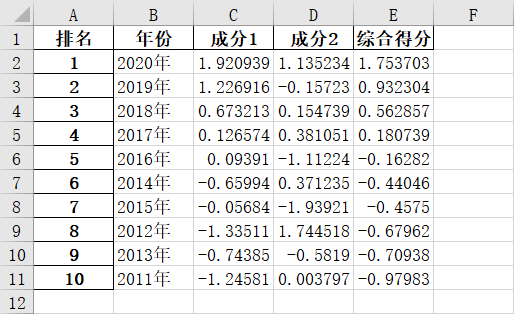
一、源数据 二、SPSS因子分析 2.1.导入数据 2.2.标准化处理 由于指标的量纲不同（单位不一致），因此，需要对数据进行标准化处理 2.3.因子分析 点击“确定”后，再回到“总方差解释”表格，以“旋转载荷平方和”中的各成分因子贡献率为权重，对因子得分做加权平均处理，可计算出综合得分 即：综合得分=(0.72283 * FA
因子分析（Factor Analysis）
因子分析是一种统计分析方法，用于确定一组变量与一组潜在构造因子之间的关系。它可以帮助我们了解变量之间的相关性和隐藏在变量背后的潜在结构。通过因子分析，我们可以将一组相关的变量简化为更少的因子，从而降低数据的复杂性，并揭示出变量之间的共同特征。因子分析可以应用于各种领域，如心理学、教育、市场调研等。 因子分析的特点如下： 1. 变量简化：因子分析可以将一组相关的变量简化为较少的因子，减少了变量的复
数学建模【因子分析】
一、因子分析简介 因子分析由斯皮尔曼在1904年首次提出，其在某种程度上可以被看成是主成分分析的推广和扩展。 因子分析法通过研究变量间的相关系数矩阵，把这些变量间错综复杂的关系归结成少数几个综合因子，由于归结出的因子个数少于原始变量的个数，但是它们又包含原始变量的信息，所以，这一分析过程也称为降维。由于因子往往比主成分更易得到解释，故因子分析比主成分分析更容易成功，从而有更广泛的应用。
因子分析、主成分分析（PCA）、独立成分分析（ICA）——斯坦福CS229机器学习个人总结（六）
因子分析是一种数据简化技术，是一种数据的降维方法。 因子分子可以从原始高维数据中，挖掘出仍然能表现众多原始变量主要信息的低维数据。此低维数据可以通过高斯分布、线性变换、误差扰动生成原始数据。 因子分析基于一种概率模型，使用EM算法来估计参数。 主成分分析（PCA）也是一种特征降维的方法。 学习理论中，特征选择是要剔除与标签无关的特征，比如“汽车的颜色”与“汽车的速度”无关； PCA中要处
【数学建模】《实战数学建模：例题与讲解》第十二讲-因子分析、判别分析（含Matlab代码）
【数学建模】《实战数学建模：例题与讲解》第十二讲-因子分析、判别分析（含Matlab代码） 基本概念时间判别费歇判别贝叶斯判别 习题10.31. 题目要求2.解题过程3.程序4.结果 习题10.6（1）1. 题目要求2.解题过程——对应分析3.程序4.结果 习题10.6（2）1. 题目要求2.解题过程——R型因子分析3.程序4.结果 习题10.6（3）1. 题目要求2.解题过程——聚类分析
因子分析Factor analysis
简介：本文主要介绍EM算法求解因子分析问题 因子分析Factor analysis 在文章 EM算法 求解混合高斯模型时，通常假设拥有足够多的样本去构造这个混合高斯分布，即样本数量n要远大于样本维数d： 如果样本数量小于样本维数，那么协方差矩阵 是奇异矩阵,那么 和都无法计算。在因子分析中，一个d维的向量通常由一个k维向量生成，通常k远小于d。具体模型如公式1所示: 公式1
斯坦福大学机器学习——因子分析（Factor analysis）
一、问题的提出 在EM算法求解高斯混合模型一文中，我们的样本集 ，而样本的数量m远大于样本的维度n，因此，可以轻易的构造出高斯混合模型。 现在，我们再看下不同的情况：假如，或，我们将很难构建一个普通高斯模型，更别提高斯混合模型。这m个的数据仅仅是 的子空间，如果我们用这m个数据建立高斯模型，并对利用极大似然，对期望和方差进行参数估计。可得： 我们将发现协方差为奇异矩
基于机器学习的居民消费影响因子分析预测
项目视频讲解： 基于机器学习的居民消费影响因子分析预测_哔哩哔哩_bilibili 主要工作内容： 完整代码： import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport seaborn as snsimport missingno as msnoimport warningswarn
数据挖掘——宁县（区、市）农村居民人均可支配收入影响因子分析（论文）
《数据挖掘与分析》课程论文 题目：宁县（区、市）农村居民人均可支配收入影响因子分析 xx学院xx班：xxx 2022年6月 摘要：农村居民人均可支配收入可能被农作物产量、牲畜存栏、农作物播种数量等诸多因素影响。为此，本文利用逐步回归分析法分析了宁县1989-2001年8个因素对农村居民人均可支配收入的影响，最后结论表明，总人口数、农业人口数、大牲畜存栏量都对农村居民人均可支配收
因子分析的一个小例子
这是学习笔记的第 1997 篇文章 今天做了下因子分析中的东东，本来想找一些公共网站的数据，限于时间和要做一些数据整理，时间来不及，就找了一个现成的数据源。 这是洛杉矶等十二个大都市的人口调查获得的，包含了5个社会以经济变量：人口总数，居民受教育年限，佣人总数，服务行业人数，中等的房价。 为了方便我把数据集先提供出来。 人口(X1)教育年限(X2)佣人数(X3)服务人
R语言对混合分布中的不可观测与可观测异质性因子分析
最近我们被客户要求撰写关于利率制定的研究报告，包括一些图形和统计输出。 今天上午，在课程中，我们讨论了利率制定中可观察和不可观察异质性之间的区别（从经济角度出发）。为了说明这一点，我们看了以下简单示例。让 X 代表一个人的身高。考虑以下数据集 > Davis[12,c(2,3)]=Davis[12,c(3,2)] 在这里，关注变量是给定人的身高， > X=Davis$heigh
【转载】因子分析（Factor Analysis）
因子分析（Factor Analysis） 【pdf版本】因子分析 1 问题 之前我们考虑的训练数据中样例的个数m都远远大于其特征个数n，这样不管是进行回归、聚类等都没有太大的问题。然而当训练样例个数m太小，甚至m<<n的时候，使用梯度下降法进行回归时，如果初值不同，得到的参数结果会有很大偏差（因为方程数小于参数个数）。另外，如果使用多元高斯分布(Multivariate Gaus
用极大似然法估计因子载荷矩阵_多元统计分析第13讲（因子分析：载荷矩阵的估计，因子旋转；典型相关分析基本思想）...
8.3 因子载荷矩阵的估计方法 (一)主成分分析法 回顾一下主成分法估计因子载荷矩阵的步骤：求出原变量协方差阵(或相关阵)的前 m 个特征根(考虑累积贡献率)，后面的特征根忽略掉 因子载荷矩阵的每一列为前 m 个特征根乘上对应的单位特征向量 特殊因子的方差为 1 - 共同度(即因子载荷该行的平方和) 用原协方差阵减去公因子协方差阵与特殊因子协方差阵，得到残差阵 残差阵元素的平方和为残差平方和
python - 多因子分析
#!/usr/bin/env python3# -*- coding: utf-8 -*-import pandas as pdimport numpy as npimport scipy.stats as ss## 正态分布norm_dist = ss.norm.rvs(size=20)Normal = ss.normaltest(norm_dist)Normal,Pvalue =