本文主要是介绍R语言对混合分布中的不可观测与可观测异质性因子分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近我们被客户要求撰写关于利率制定的研究报告,包括一些图形和统计输出。
今天上午,在课程中,我们讨论了利率制定中可观察和不可观察异质性之间的区别(从经济角度出发)。为了说明这一点,我们看了以下简单示例。让 X 代表一个人的身高。考虑以下数据集
> Davis[12,c(2,3)]=Davis[12,c(3,2)]
在这里,关注变量是给定人的身高,
> X=Davis$height
如果我们看直方图,我们有
> hist(X,col="light green", border="white",proba=TRUE,xlab="",main="")
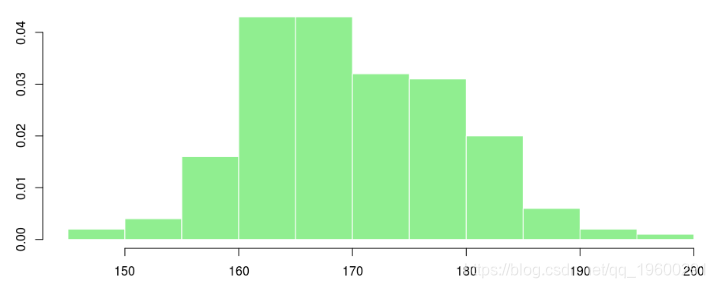
我们可以假设我们具有高斯分布吗?
在这里,如果我们拟合高斯分布,将其绘制出来,并添加基于核的估计量,我们将得到
> (param <- fitdistr(X,"normal")$estimate)
> f1 <- function(x) dnorm(x,param[1],param[2])
> x=seq(100,210,by=.2)
> lines(x,f1(x),lty=2,col="red")
> lines(density(X))这篇关于R语言对混合分布中的不可观测与可观测异质性因子分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


