本文主要是介绍因子分析模板,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
因子分析的模板
2011A-2模板论文 P10
因子分析的主要步骤如下:
- 数据标准化
由于不同重金属元素的量纲可能不同, 因此为了消除量纲对数据的影响, 对所有的重金属采用下面的公式对数据进行归一化处理:

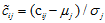
其中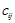
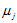
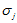
2.计算协方差矩阵S
因为已经对数据进行归一化处理,协方差的大小在一定程度上表示了个元素之间的关系,记每个区有n个采样点,则协方差表达式如下:
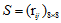
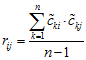
3. 计算初等载荷矩阵 A
计算矩阵S的特征值 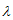
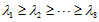
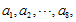

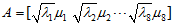
4. 主因子个数确定及因子旋转
根据初等载荷矩阵,计算各个主因子的贡献率。同时为了更好的解释因子的现实意义,利用具有 Kaiser 标准化的正交旋转法,对提取的因子载荷矩阵进行旋转,得到矩阵B,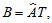
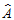
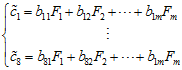
其中,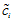
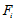
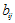
相关的代码:
load data.txt %把原始数据保存在纯文本文件data.txt中
data=reshape(data,[16,5]);
m=size(data,1);
x=data(:,5);data=data(:,1:4),num=2; %num 代表的因子的个数
data=zscore(data); %数据标准化
r=cov(data);
[vec,val,con]=pcacov(r); %进行主成分分析的相关计算
val,con
f1=repmat(sign(sum(vec)),size(vec,1),1);
vec=vec.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec,1),1);
a=vec.*f2 %载荷矩阵
%求得载荷矩阵,该载荷矩阵是没有进行旋转变换的因子
%如果指标变量多,选取的主因子个数少,可以直接使用factoran进行因子
%分析
%本题中4个指标变量,选取2个主因子,factoran无法实现
%下面在因子旋转中,由于num=2,所以只对前面两个进行旋转,换面的保持布
%标。
[b,t]=rotatefactors(a(:,1:num),'method', 'varimax') %旋转变换
bz=[b,a(:,num+1:end)] ;%旋转后的载荷矩阵
gx=sum(bz.^2); %计算因子贡献
gxv=gx/sum(gx); %计算因子贡献率
dfxsh=inv(r)*b; %计算得分函数的系数
df=data*dfxsh ;%计算各个因子的得分
%后面是评价模型
zdf=df*gxv(1:num)'/sum(gxv(1:num)); %对各因子的得分进行
加权求和
[szdf,ind]=sort(zdf,'descend') %对企业进行排名
xianshi=[df(ind,:)';zdf(ind)';ind'] %显示计算结果
[x_zdf_coef,p]=corrcoef([zdf,x]) %计算相关系数
[d1,d1int,d2,d2int,stats]=regress(zdf,[ones(m,1),x]) %回归分析计算
函数说明reshape:
close all; clear; clc;
A = [1 2 3; 4 5 6; 7 8 9; 10 11 12] % 4 by 3
B = reshape(A, 2, 6) % 2 by 6
% C = reshape(A, 2, 4) % error
% D = reshape(A, 2, 10) % error
E = reshape(A, 2, 3, 2) % 2 by 3 by 2
注意:reshape函数对原数组的抽取是按照列抽取的(对原数组按列抽取,抽取的元素填充为新数组的列)
运行结果:
这篇关于因子分析模板的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






