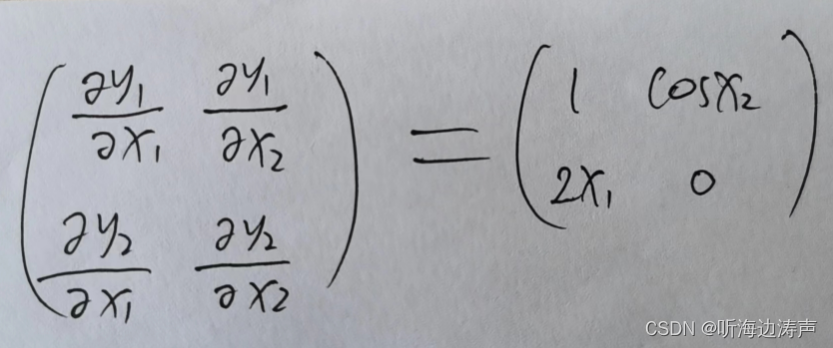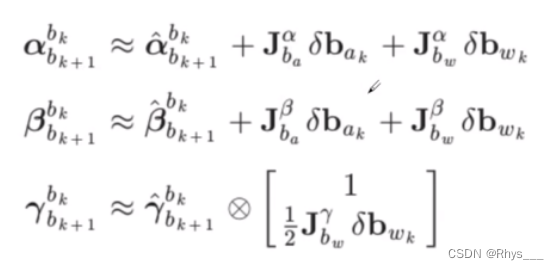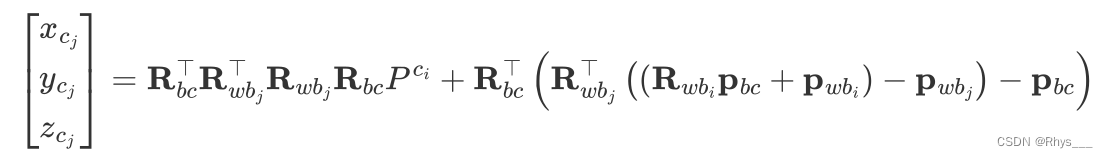可比专题
Python和C++(CUDA)及Arduino雅可比矩阵导图
🎯要点 对比三种方式计算读取二维和三维三角形四边形和六面体网格运动学奇异点处理医学图像成像组学分析特征敏感度增强机械臂路径规划和手臂空间操作变换苹果手机物理稳定性中间轴定理 Python雅可比矩阵 多变量向量值函数的雅可比矩阵推广了多变量标量值函数的梯度,而这又推广了单变量标量值函数的导数。换句话说,多变量标量值函数的雅可比矩阵是其梯度(的转置),而单变量标量值函数的梯度是其导数。 在
【数值计算方法】雅可比解线性方程
废话少说,直接上干货。 #include <stdio.h>#include <stdlib.h>#include <math.h>#define MaxSize 100double A[MaxSize][MaxSize]; //系数矩阵double B[MaxSize]; //系数矩阵double C[MaxSize][MaxSize]; //去对角线矩阵d
机械臂雅可比矩阵的矢量积理解和matlab实现
雅可比矩阵的第Ji列: 关于一些基本概念可以参考博客,部分细节如下: 每个移动关节,Ji可以这样计算: 每个旋转关节,Ji这样计算: 有时候要求按照末端执行器坐标系{n}来执行一些位移旋转之类的操作,在末端执行器坐标系下的雅可比矩阵可以这样计算: SDH代码程序参考博客,如下: function [ J ] = Jacob_cross_SDH( q )%JACOB_CROSS_S
C#,数值计算——计算实对称矩阵所有特征值和特征向量的雅可比(Jacobi)方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// Computes all eigenvalues and eigenvectors of /// a real symmetric matrix by Jacobi's method. /// </summary>
雅可比矩阵(Jacobian Matrix)
假设给定一个从n维欧式空间到m维欧式空间的变换: 雅可比矩阵就是将一阶偏导数排列成一个m行、n列形式的矩阵,记作: 举一个例子: 雅可比矩阵等于:
VINS-Mono-后端优化 (二:预积分残差雅可比推导)
文章目录 对位置 δ α \delta\alpha δα 进行求导位置误差 δ α \delta\alpha δα 对平移 P b k w P^{w}_{b_{k}} Pbkw 的求导位置 δ α \delta\alpha δα 对旋转 R w b k R^{b_{k}}_{w} Rwbk 进行求导 对速度 δ β \delta\beta δβ 进行求导速度 δ β \
VINS-Mono-后端优化 (三:视觉雅可比推导)
用逆深度是因为这样可以在优化中从优化3个变量降低到1个,降低优化的维度加快求解速度 用逆深度是因为当距离很远的时候, 1 x \frac{1}{x} x1 x x x 就会无穷大,而3D点很近的情况也一般不会有,这也是为了数值稳定性 用逆深度的话就要和其中一帧进行绑定,这个就是和观测到该点的第一帧进行绑定,这样才能表示一个3D点信息 划窗中维护的全部都是IMU下的位姿,所以相机要通过外参变
计算机数值方法-雅可比迭代和高斯赛德尔迭代
算法流程 其实迭代法前面已经学习过啦,这里的迭代是在前面迭代的基础上的高阶形式——即解决线性方程组的问题。 下面简单介绍雅克比迭代的基本流程。 雅可比迭代 有一线性方程组, A x = b Ax=b Ax=b,其中: 我们可以将其化为以下形式: x i = B x j + f , ( i = 1 , 2 , 3...... n , j = 1 , 2 , 3 , ¬ i . . . .