一，变化率的介绍 这里我们要考虑一个函数，它表示一些量，其变化为x不同。例如，也许f(x)表示x纪要。或者是汽车行驶的距离x小时。在这两个例子中，我们使用了x来表示时间。答案是肯定的x不必表示时间，但它可以生成易于可视化的示例。 我们在这里要做的是确定多快f(x)在某个时候发生变化，比如x=a.这称为瞬时变化率，有时简称为瞬时变化率f(x)在x=a. 与切线问题一样，此时我们能做的就是估计变

我们将看看微积分研究中两个相当重要的问题。现在关注这些问题有两个原因。 第一个问题：切线 我们要研究的第一个问题是切线问题。在讨论这个问题之前，最好定义一条切线。 函数的切线f(x)在点上x=1，是一条刚好在相关点接触函数图形的线，并且与该点的图形“平行”（以某种方式）。请看下面的图表。 from manim import * class TangentLineScene01(Scene

切线 要求与曲线 C C C相切于 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))点的切线，我们可以在曲线上找到与之相近的一点 Q ( x , f ( x ) ) Q(x, f(x)) Q(x,f(x))，然后求出割线 P Q PQ PQ的斜率： m P Q = f ( x ) − f ( a ) x − a m_{PQ} = \frac{f(x) - f(a)}

四元数乘法 这里首先需要介绍四元数乘法，假设有两个四元数 q a , q b q_a, q_b qa​,qb​，如下所示： q a = q a 0 + q a 1 i + q a 2 j + q a 3 k = [ s a , v a ] T q b = q b 0 + q b 1 i + q b 2 j + q b 3 k = [ s b , v b ] T \begin{aligned}

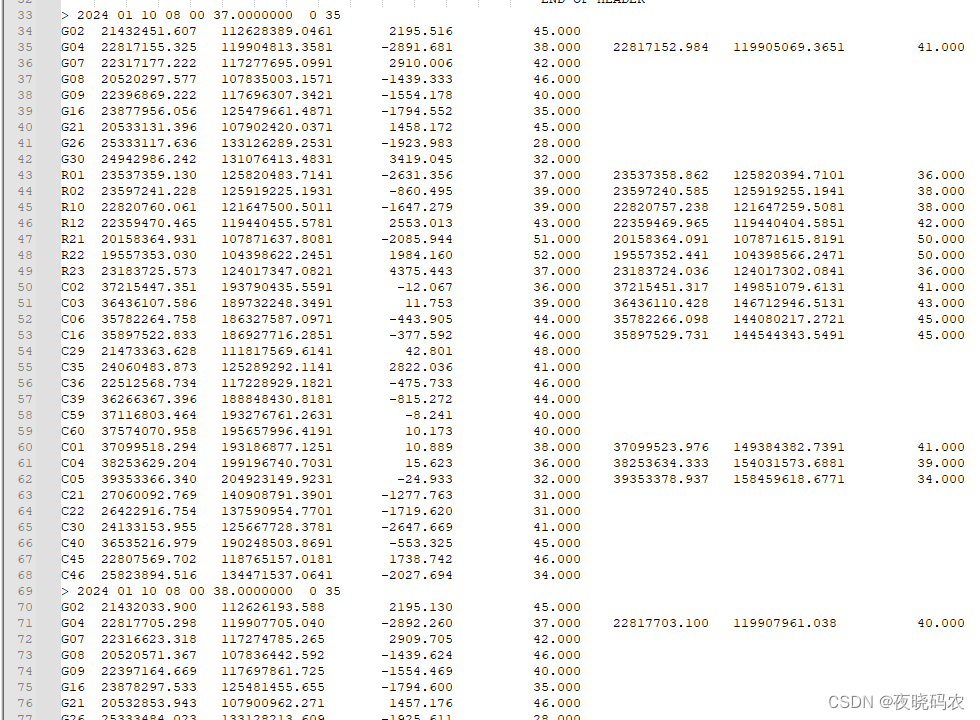
概述 因为在做公司项目的时候，遇到一些接收机吐出来的多普勒数据存在异常的情况，后面咨询各个大佬需求验证方法，大佬耐心回了句“利用历元间伪距数据计算伪距变化率，然后将伪距变化率转成多普勒比对即可”，听到大佬的回答，我是一脸懵逼的，一通百度找到具体的换算方法，故而博文记录，用于备忘。 注意： 这是一个纯GNSS小白的博文记录，大佬出门左转哈 数据 计算方法 计算公式（非科学严谨版本） （

本文内容 函数的回顾方向导数的回顾从变化率的角度认识一下向量从变化率的角度认识一下梯度梯度下降的另一种认识 一直以来我对于梯度这个更多是几何概念的物体和偏导数（变化率）的联系充满了困惑，最近重新学习线性回归，在复习梯度下降的时候，查阅了一些资料，重新在变化率的角度上认识了向量，充分理解了梯度和偏导数的联系。故根据一些感悟，书写此文，供大方之家批评指导 写在最前 最近在看《西学门径》，其中有