初等专题
CSP-J基础之数学基础 初等数论 一篇搞懂(一)
文章目录 前言声明初等数论是什么初等数论历史1. **古代时期**2. **中世纪时期**3. **文艺复兴与近代**4. **现代时期** 整数的整除性约数什么样的整数除什么样的整数才能得到整数?条件:举例说明:一般化: 判断两个数能否被整除 因数与倍数质数与复合数使用开根号法判定质数哥德巴赫猜想最大公因数与辗转相除法计算最大公因数的常用方法:举几个例子:例子 1: 计算 12 和 18
CSP-J基础之数学基础 初等数论 一篇搞懂(二)
文章目录 前言算术基本定理简介什么是质数?举个简单例子:重要的结论:算术基本定理公式解释:举例: 算术基本定理的求法如何找出质因数:举个简单的例子: 重要的步骤:C++实现 同余举个例子:同余的性质简介1. 同余的自反性2. 同余的对称性3. 同余的传递性4. 同余的加法性质5. 同余的乘法性质 推论 总结 前言 在计算机科学和数学中,初等数论是一个重要的基础领域,涉及到整数
蓝桥杯之初等数论(二)
上一篇:蓝桥杯之初等数论(一)讲了两种知识点,即素数和合数的判断,最大公约数和最小公倍数的判断,接下来,我继续讲解有关初等数论的有关知识点。 什么是同余定理: 同余定理,也称为模运算定理或同余式定理,是数论中的一个重要概念。它主要涉及到整数之间的某种等价关系,即两个整数除以同一个正整数,如果所得的余数相同,则称这两个整数对于该正整数同余。同余关系是一种等价关系,满足反身性、对称性和传递性。
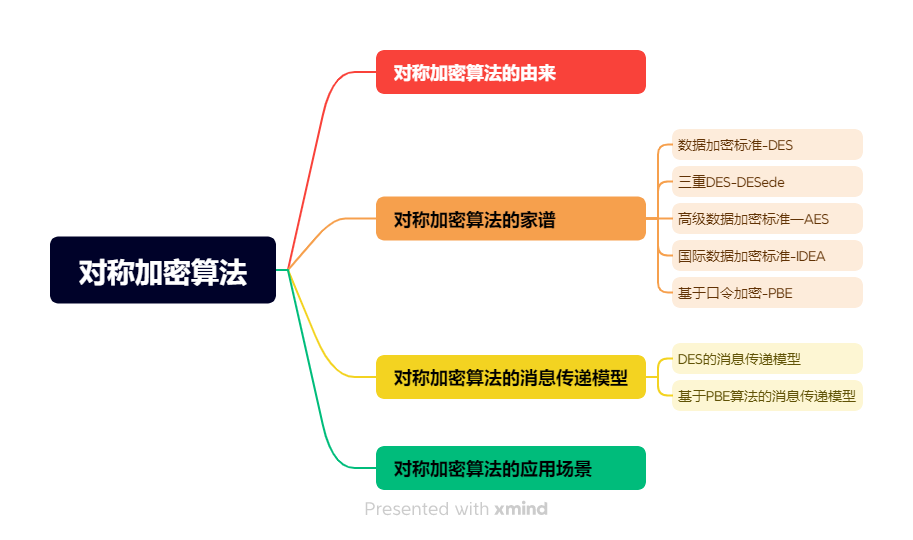
密码学:一文看懂初等数据加密一对称加密算法
文章目录 对称加密算法简述对称加密算法的由来对称加密算法的家谱数据加密标准-DES简述DES算法的消息传递模型DES算法的消息传递过程和Base64算法的消息传递模型的区别 算法的实现三重DES-DESede三重DES-DESede实现 高级数据加密标准一AES实现 国际数据加密标准-IDEA实现 基于口令加密-PBE基于PBE算法的消息传递模型 应用场景相关的Java API使用手册参
数学分析(一)-实数集与函数3-函数概念6-初等函数4-三角函数6:arccotx【cotx的反函数】【减函数】【定义域:(-∞,+∞);值域:(0,π)】【arccot0=π/4】
高中数学,三角函数的图像与性质 系统化,轻快学习高中数学三角函数的图像、性质及其变换必备知识 精准狠——三角函数图像及其性质 三角函数与反三角函数(图像)
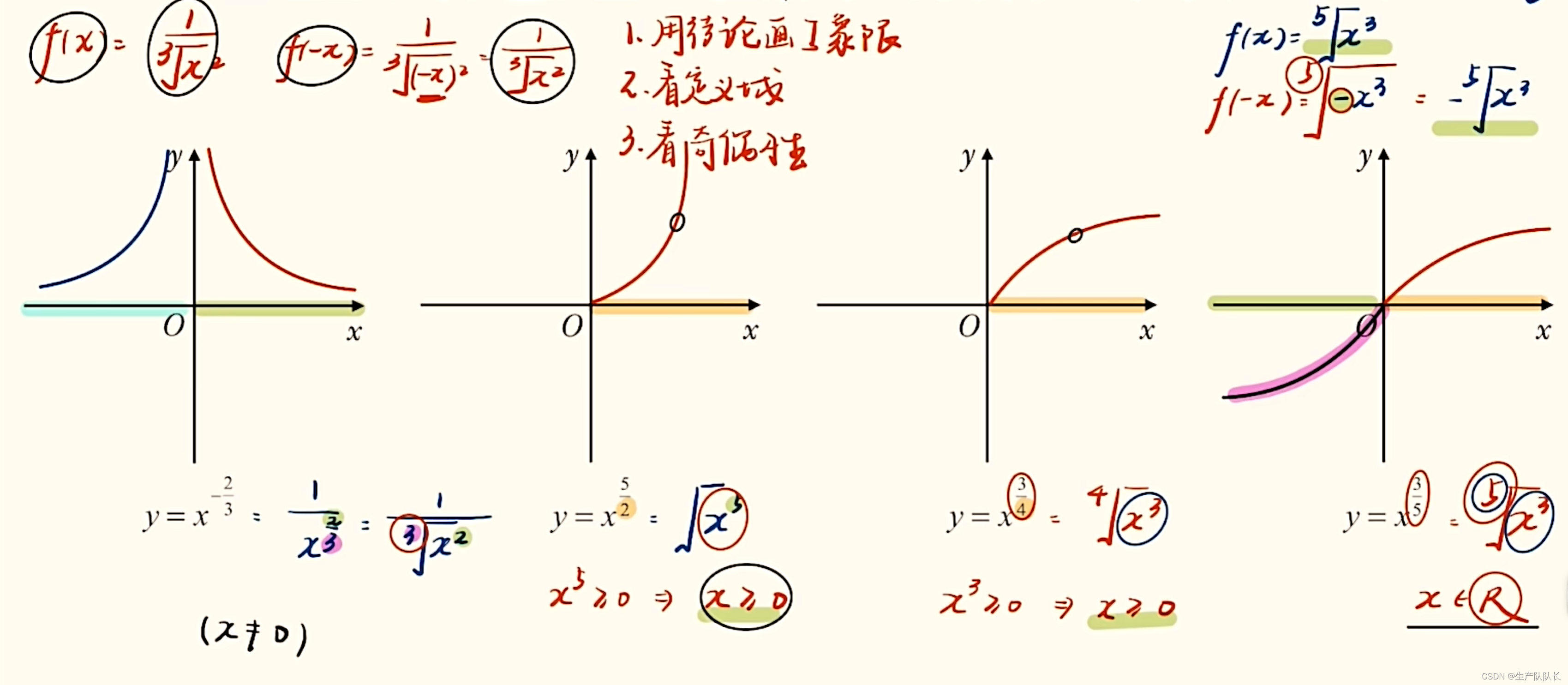
高中数学:初等函数之幂函数
1、定义 注意:x项系数,只能是1! 例题: 2、常见幂函数图像 3、分数指数幂 x定义域:分母为偶数时,如:2、4、6等,则x≥0 x≥0时 4、画草图 步骤: 1、利用结论画出第一象限草图。 2、判断定义域。 3、根据奇偶性画其他象限草图。 1、第一象限草图(一般性结论) 2、定义域 对于分母为偶数的分式幂函数,它的定义域是x≥0,所以,只有第一象限有图像
【线代】为什么初等行变换不改变列向量/行向量的线性相关性?特征方程的简便设法?
线代中其他的一些遗留小问题,后续可能会更新。 1. 初等行变换不改变什么?(初等列变换同理) 初等行变换不改变列向量的线性相关性,也不改变行向量的线性相关性。可从以下两点来看。 ① 初等变换不改变矩阵的秩,矩阵的秩=列秩=行秩。而相关性就体现为是否满秩。 ② 不改变列向量的相关性,是因为初等行变换的过程始终保持了与原方程组同解,所以列向量间的线性关系(就是系数x1,x2……的取值,就
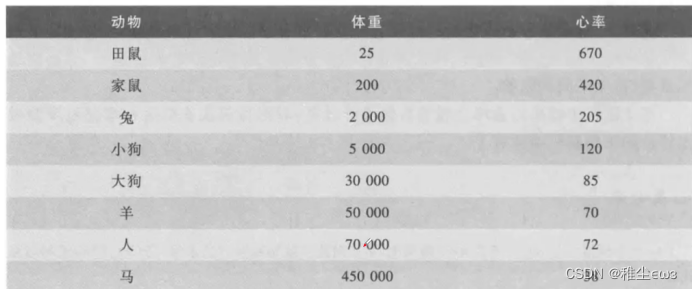
动物体重-心率关系模型建立初等模型
1 问题描述 动物体重-心率关系模型:生物学家认为,对于休息状态的热血动物,消耗的能量主要用于维持体温,能量与从心脏到全身的血流量成正比,而体温主要通过身体表面散失,建立一个动物体重(单位:g)与心率(单位:次/min)之间关系的模型,并用下面的数据加以检验。 2 模型假设 假设热血动物在休息状态时消耗的能量全部转换为热量,全部热量都用来维持体温。(2)假设动物的体重完全与
初等模型——公平的奖学金名额分配
目录 一、问题 二、公平分配方法 ①我们先按照比例来分: ②公平分配方法: 三、计算和结果 先说一下,本篇是学校上课内容个人的整理笔记。 一、问题 三个系学生共200名(甲系100,乙系60,丙系40),20个奖学金名额,按比例分配,三个系分别为10,6,4名。现因学生转系,三系人数为103,63,34,问20个名额该如何分配? 我们按比例分配: 系别学生人数比例(%
初等数论,LeetCode 365. 水壶问题
一、题目 1、题目描述 有两个水壶,容量分别为 jug1Capacity 和 jug2Capacity 升。水的供应是无限的。确定是否有可能使用这两个壶准确得到 targetCapacity 升。 如果可以得到 targetCapacity 升水,最后请用以上水壶中的一或两个来盛放取得的 targetCapacity 升水。 你可以: 装满任意一个水壶清空任意一个水壶从一个水壶向另外一个水壶
每日编程一刷--矩阵初等行变换你会了吗?
文章目录 每日编程一刷--矩阵初等行变换你会了吗?前言总结 每日编程一刷–矩阵初等行变换你会了吗? 前言 欢迎来到每日编程一刷 基础 相信大家学了一天的高数 现代 大学生应该都是考试周了 你真的将现代知识掌握了没有 下面靠一靠大家 错误代码 以及思路…😔 误以为只需要交换相邻两列 实际上并不是 我们要进行交换的是 任意两列 下面我写的代码就太死板了 认为只能是
【初等数论】同余方程、与二次剩余互反律
同余方程、二次剩余、二次互反律 1、同余方程 剩余类可以看做是一个新的数系,它对加减乘运算是封闭的,所以同余方程对多项式是有意义的。这里我们就来讨论下一元多项式方程(1)的解,当然它的解是一个剩余类集合,最多有 m 个解。 f ( x ) = ∑ k = 0 n a
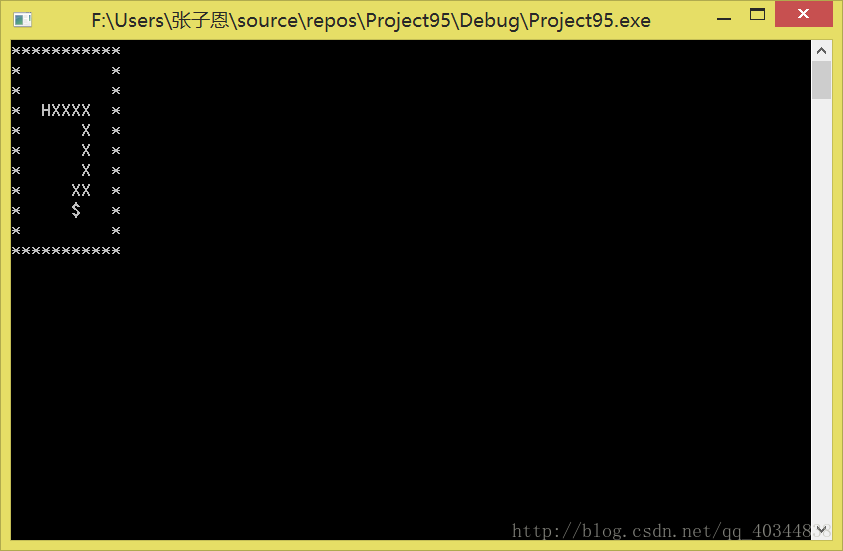
初等贪吃蛇的基本算法
作为一个渣渣程序猿,我来讲一下贪吃蛇的基本算法。 我们采用老师所讲的“逐步求精”的办法。 先找出主干 主干1: 定义蛇的基本特征: #define SNAKE_HEAD 'H'#define SNAKE_BODY 'X'#define BLANK_CELL ' '#define WALL_CELL '*'#define food $ 主干2: 做出矩阵图: cha
《数学模型(第五版)》学习笔记(1) 第1章 建立数学模型 第2章 初等模型
参考数学建模论坛《数学模型(第三版)》学习笔记 http://www.madio.net/thread-146480-1-1.html 参考视频 数模视频(姜启源、谢金星) https://www.bilibili.com/video/BV1VJ411w7r3/?spm_id_from=333.788.recommend_more_video.0&vd_source=3ef6540f8473c73
初等数论中整除性规律证明
依稀记的学习初等数学整数性质的时候,只学到了能够被2,3,5整除的整数的特点,但是根据网上搜索到的资料,似乎这个规则可扩充到除了7之外的所有十以内的自然数,下面这些规则可以用于检验一个整数是否能够被另一个整数整除,以及帮助我们找到一些特殊的整数。 如果一个整数能够被2整除,那么这个整数的末位数字必须是0,2,4,6或者8。如果一个整数能够被3整除,那么这个整数各个数位上的数字之和必须能够被3整除
初等数论以及欧几里德定理的证明
欧几里德定理(无限质数定理) 质数的个数是无限的吗?还是说存在一个最大的质数,比它大的任何数字都可以表示为已有质数的乘积?首先提出这个问题的正式欧几里得本人,他以一种简单而优雅的方式证明了质数有无穷多个,所以并不存在所谓的”最大质数”。为了验证这个命题,我们暂且假设质数的个数是有限的,并用字母N来达标已知最大的质数。现在我们将所有质数相乘,最后再加1,数学表达式如下: 这个式子得出的结果当
EM@分段函数复合的基本问题@函数间的初等运算
文章目录 abstract分段函数的一般表示 分段函数复合的基本问题分析算法例例 函数的初等运算构成的函数复合函数的定义域函数的运算 abstract 复合函数和分段函数的表示和应用 复合函数中我们讨论过函数 g , f g,f g,f复合为 f ∘ g f\circ{g} f∘g的条件是 R g ∩ D f = ∅ R_{g}\cap{D_f}=\emptyset Rg