初等数论中整除性规律证明

本文主要是介绍初等数论中整除性规律证明，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

依稀记的学习初等数学整数性质的时候，只学到了能够被2，3，5整除的整数的特点，但是根据网上搜索到的资料，似乎这个规则可扩充到除了7之外的所有十以内的自然数，下面这些规则可以用于检验一个整数是否能够被另一个整数整除，以及帮助我们找到一些特殊的整数。

如果一个整数能够被2整除，那么这个整数的末位数字必须是0，2，4，6或者8。
如果一个整数能够被3整除，那么这个整数各个数位上的数字之和必须能够被3整除。
如果一个整数能够被4整除，那么这个整数的最后两位数字必须能够被4整除。
如果一个整数能够被5整除，那么这个整数的末位数字必须将是0或者5。
如果一个整数能够被6整除，那么这个整数必须同时满足将能够被2和3整除。
如果一个整数能够被8整除，那么这个整数的最后三位数字必须能够被8整除。
如果一个整数能够被125整除，那么这个整数的最后三位数字必须能够被125整除。
如果一个整数能够被9整除，那么这个整数各个数位上的数字之和必须能够被9整除。
如果一个整数能够被10整除，那么这个整数的末尾数字必须是0。
如果一个整数它的末两位数可以被25整除，则它能被25整除。

简单证明一下，需要用到四个引理，如下：

引理1：

假设有两个整数a和b,以及除数c,那么说：

$(a\times b)\ mod\ c = [(a\ mod \ c)\ \times\ (b\ mod \ c) ]\ mod \ c$

这句话的意思是，两个整数的积对一个数取模，等于这两个数字分别对这个数取模结果的积，再对这个数取模。

$a=y\times c+ r$

$b=z\times c + s$

其中y,z表示a,b分别除以c的商，r,s则是余数，将上面两个式子带入，则：

$(a\times b)\ mod\ c =[(y\times c+ r)\times (z\times c+ s)]\ mod\ c=(r\times s)\ mod \ c$

而：

$[(a\ mod \ c)\ \times\ (b\ mod \ c) ]\ mod \ c = [r \times s]\ mod \ c=(r\times s)\ mod \ c$

所以引理得证明。

引理2：

$(a+b)\ mod \ c =(y\times c+ r + z\times c+ s)\ mod \ c =(r+s)\ mod \ c$

$a \ mod \ c =(y\times c+ r) \ mod \ c=r$

$b \ mod \ c =(z\times c+ s) \ mod \ c=s$

$[(a\ mod \ c)\ +\ (b\ mod \ c) ]\ mod \ c =[r+s]\ mod \ c= (r+s)\ mod \ c$

所以：

$(a+b)\ mod \ c =[(a\ mod \ c)\ +\ (b\ mod \ c) ]\ mod \ c$

引理3：

$(a\times b)\ mod \ c = [a\times (b\ mod \ c)]\ mod \ c$

证明：

$\\ (a\times b)\ mod \ c = [a\times (z\times c + s)] \ mod \ c=(a\times s)\ mod \ c=[(y\times c+ r) \times s]\ mod \ c=(s\times r)\ mod \ c$

$[a\times (b\ mod \ c)]\ mod \ c = (a\times s )\ mod\ c=(s\times r)\ mod \ c$

引理4：

$(a+b)\ mod\ c = [(a \ mod \ c )+ (b\ mod \ c)] \ mod \ c$

证明：

$[(a \ mod \ c )+ (b\ mod \ c)] \ mod \ c=(y\times c+ r+z\times c+ s)\ mod \ c = (r+s)\ mod \ c$

$[(a \ mod \ c )+ (b\ mod \ c)] \ mod \ c = [s +r]\ mod \ c$

引理证明完毕，现在证明上面的9个整除性规则，假设任意一个n位的十进制数：

$\boldsymbol{a_{n-1}a_{n-2}a_{n-3}\cdots a_3a_2a_1a_0 = a_{n-1}10^{n-1}+a_{n-2}10^{n-2}+a_{n-3}10^{n-3}+\cdots a_310^3+a_210^2+a_110^1+a_0 = \sum_{i=0}^{n-1}a_{i}10^i}$

被2整除的条件：

$\\ \boldsymbol{\bigg(\sum_{i=0}^{n-1}a_{i}10^i\bigg)\ mod 2=\bigg(\sum_{i=1}^{n-1}a_{i}10^i+a_0\bigg)\ mod 2 = \bigg(\sum_{i=1}^{n-1}a_{i}10^i\bigg)\ mod 2+\bigg(a_0\bigg)\ mod 2 = 0 + \bigg(a_0\bigg)\ mod 2=a_0\ mod 2}$

所以，判断一个数能否被2整除只需要判断个为即可，一个整数可以被2整除等价于个位可以被整除，而个位被整除的条件我们通过枚举很容易得到这个充要条件，也就是数字0，2，4，6，8。进而得到，任何整数被2整除的充分必要条件是个为的数字为0，2，4，6，8中的一个。

被3整除的条件：

$\\ \boldsymbol{\bigg(\sum_{i=0}^{n-1}a_{i}10^i\bigg)\ mod 3=\bigg(\sum_{i=1}^{n-1}a_{i}10^i+a_0\bigg)\ mod 3 =\bigg[a_0 + (9+1)a_1+(99+1)a_2+(999+1)a_3+\cdots +(9999\cdots 999 + 1)a_{n-1}\bigg]\ mod 3 }\\=\bigg[a_0 + a_1+a_3+\cdots + a_{n-1}\bigg] \ mod 3 = (a_0 + a_1+a_3+\cdots + a_{n-1})\ mod 3$

所以，被3整除的充分必要条件是，各个数位的数字加和能够被3整除。

被9整除的条件：

$\\ \boldsymbol{\bigg(\sum_{i=0}^{n-1}a_{i}10^i\bigg)\ mod 9=\bigg(\sum_{i=1}^{n-1}a_{i}10^i+a_0\bigg)\ mod 9 =\bigg[a_0 + (9+1)a_1+(99+1)a_2+(999+1)a_3+\cdots +(9999\cdots 999 + 1)a_{n-1}\bigg]\ mod 9 }\\=\bigg[a_0 + a_1+a_3+\cdots + a_{n-1}\bigg] \ mod 9= (a_0 + a_1+a_3+\cdots + a_{n-1})\ mod 9$

所以，和被3整除的情况类似，被9整除的充分必要条件是，各个数位的数字加和能够被9整除。

根据同样的思路，被4，5，6，8整除的条件显而易见，不再证明。

被7整除的条件

文章开头列出的整除规律唯独没有7，因为7的整除规律描述起来比较复杂，如下：

设正整数

$a=a_n1000^n +a_{n-1}1000^{n-1}+\cdots + a_11000+a_0, \ \ 0\leq a_i< 1000$

则7,11,13整除a的充要条件是7,11,13整除：

$(a_0+a_2+a_4+\cdots)-(a_1+a_3+a_5+\cdots)=\sum_{i=0}^{n}(-1)^ia_i$

比如123456789是否能整除7,只需要计算789+123-456=456， 456 mod 7 = 1.所以123456789一定不被7整除.

证明过程其实很简单：

$1000\equiv(-1)mod\ 7 \\ 1000^i\equiv(-1)^imod\ 7 \\ a_i1000^i\equiv a_i(-1)^imod\ 7$

$\sum_{i=0}^{n}a_i1000^i\equiv \sum_{i=0}^{n}a_i(-1)^i \ mod \ 7$

得证。

生活中有很多同余运算应用的例子，比如教师中的列号和座位号对列数同余：

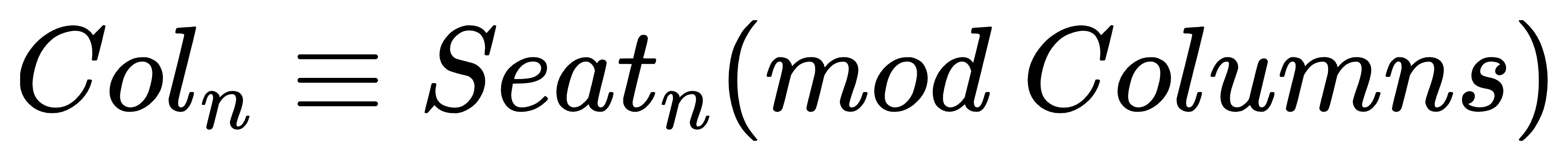
Linux系统中虚拟地址和物理地址对页面大小同余：

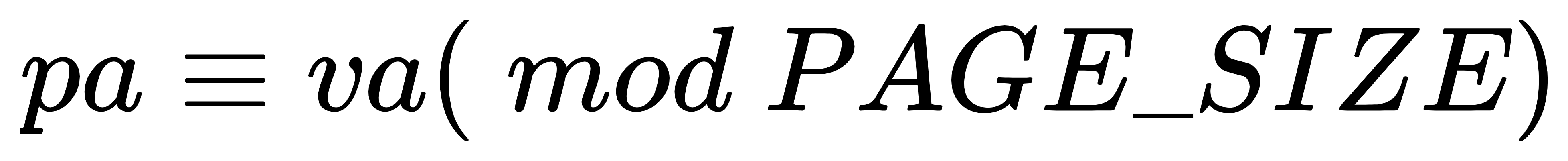
同余

$a \equiv a \ (mod \ c) \\ b \equiv b \ (mod \ c) \\ a+b\equiv [a \ mod \ c +b \ mod \ c]\ (mod \ c) \\ (a+b)\ mod \ c = (a \ mod \ c +b \ mod \ c) \ mod \ c$