分母专题
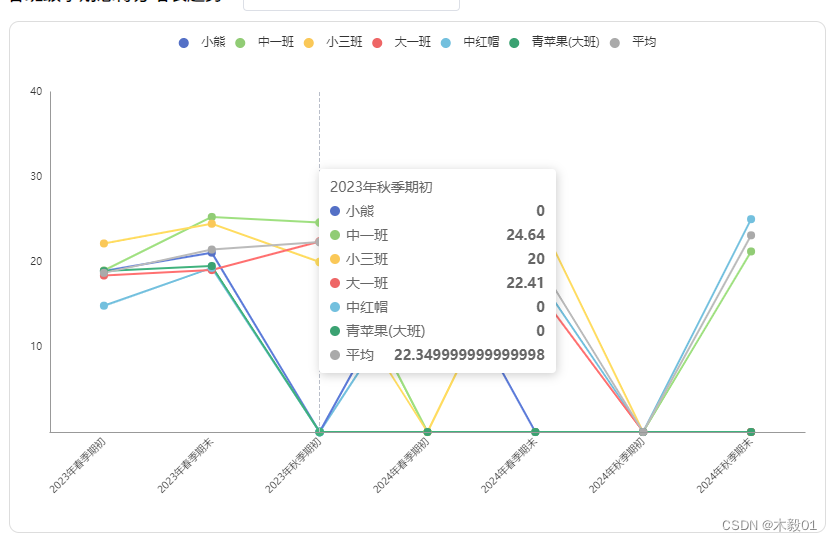
js算法 计算每一列的平均值 求matrix数组对应列的平均值 组成一个新的数组 matrix数组有6行 如果某一行里的值是0则不纳入平均的分母里
let matrix = [[18.95, 21.1, 0, 23, 0, 0, 0],[19, 25.3, 24.64, 0, 0, 0, 21.24],[22.18, 24.5, 20, 0, 26, 0, 0],[18.41, 19.05, 22.41, 27.67, 17, 0, 0],[14.86, 19.31, 0, 19.4, 18.71, 0, 25.04],[18.93, 19.
关于样本方差的分母是 ( n-1 ) 而不是 ( n )的原因
样本方差的分母是 ( n-1 ) 而不是 ( n ) 的原因与统计学中的“自由度”概念有关。使用 ( n-1 ) 作为分母可以使样本方差成为总体方差的无偏估计量。 自由度 在计算样本方差时,我们需要先计算样本均值 ( \bar{x} )。样本中的 ( n ) 个数据点中,实际上只有 ( n-1 ) 个数据点是自由变化的,因为最后一个数据点可以通过样本均值和前面的 ( n-1 ) 个数据点确定。
为什么方差的分母有时是n,有时是n-1 源于总体方差和样本方差的不同
为什么样本方差(sample variance)的分母是 n-1?样本方差计算公式里分母为n-1的目的是为了让方差的估计是无偏的。无偏的估计(unbiased estimator)比有偏估计(biased estimator)更好是符合直觉的。 因为样本用的平均值不是总体的平均值,一定会导致低估,所以我们放大一点,用n-1
矩阵的导数运算(理解分子布局、分母布局)
矩阵的导数运算(理解分子布局、分母布局) 1、分子布局和分母布局 请思考这样一个问题,一个维度为m的向量y对一个标量x的求导,那么结果也是一个m维的向量,那么这个结果向量是行向量,还是列向量呢? 答案是:行向量或者列向量皆可! 求导的本质只是把标量求导的结果排列起来,至于是按行排列还是按列排列都是可以的。但是这样也有问题,在我们机器学习算法优化过程中,如果行向量或者列向量随便写,那么结果就不
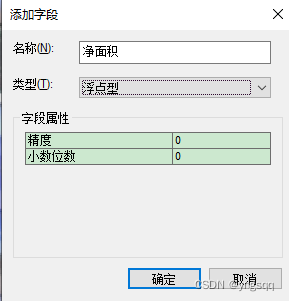
004集—二调数据库标注分子分母模式及统计净面积——arcgis
二调数据库中分子分母标注方法为: 表达式如下: "<und>"& [TBBH] &"</und>" &vbnewline& [DLBM] "<und>"&[DLBM]&"</und>" &vbnewline& [DLMC] "<und>"& [TBBH]& [QSDWMC] &"</und>" &vbnewline& [DLBM]& [DLMC] "<und>"
Java笔记(三)几种运算符介绍、分母为零的情况、标识符等
1、逻辑运算符: ^ 异或 | 简化或 & 简化并 使用“ | ”和“ & ”时,表达式的结果可以由运算符左边的操作数单独决定。 2、位逻辑运算符: ~ 按位取反 & 按位与 | 按位或
matlab问题:输出结果出现分数,且分子分母都是很长数字
当matlab计算结果出现如上图所示状况时,使用下列命令解决 format long g; %输出结果为小数 vpa(ans,5); %五位有效数字
//有一分数序列,1/2,3/2/5/3,8/5,13/8,21/13...抓住抓住求出这个数列的前20项之和。 //抓住分子分母的变化规律
//有一分数序列,1/2,3/2/5/3,8/5,13/8,21/13...抓住抓住求出这个数列的前20项之和。 //抓住分子分母的变化规律 #include<stdio.h> main() { int n,t,number=20; float a=2,b=1,s=0; for (n=1;n<=number;n++) { s=s+a/b; t=a;a=a+b;b=
高等数学:分母阶数未知,如何对分子进行泰勒展开?——对泰勒公式展开阶数问题的分析
分母阶数未知,如何对分子进行泰勒展开?——对泰勒公式展开阶数问题的分析 关于对泰勒公式的基本理解,阅读我的另一篇博客:如何理解泰勒展开公式?等价无穷小与泰勒公式的关系是什么? 题源:《1800题》P79 64题
高数 | 【极限与等价无穷小】洛必达法则的隐藏细节、广义洛必达法则(分母无穷直接洛必达)使用条件
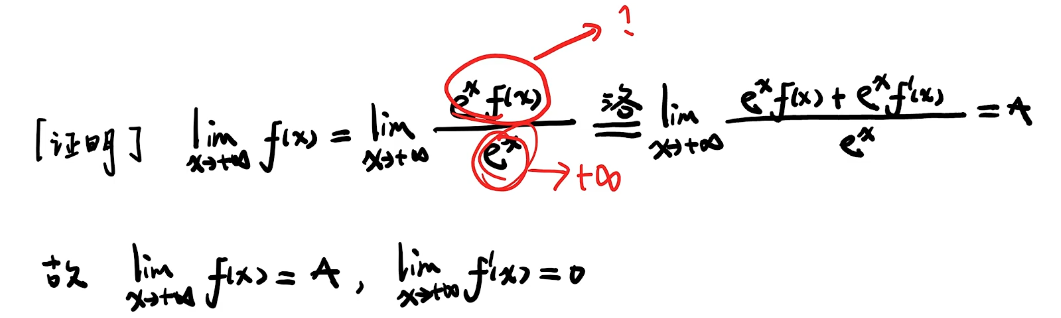
洛必达使用小结: 发现泰勒展开和等价无穷小代换都搞不定的时候,洛必达判定能否使用: 先看分母,如果趋于0,则看分子是否趋于0;如果分母趋于∞,根据广义洛必达,无需判断分子,即可使用洛必达求解。 对于一些极限类证明题,可以通过构造一个趋于无穷的分母,再使用广义洛必达获得想要的结果。 一、先看洛必达法则的内容 定理的证明:(柯西中值定理) 二、
矩阵求导的本质与分子布局、分母布局的本质
大佬讲解的实在太吊了。 就拿大佬的总结说明一下: 矩阵求导结果,无非就是分子的转置、向量化,分母的转置、向量化,它们的各种组合而已。 1、分子布局的本质:分子是标量、列向量、矩阵向量化后的列向量;分母是标量、列向量转置后的行向量、矩阵的转置矩阵、矩阵向量化后的列向量转置后的行向量。 2、分母布局的本质:分子是标量、列向量转置后的行向量、矩阵向量化后的列向量转置后的行向量;分母是标量、列向量、矩
矩阵求导中的分子布局和分母布局
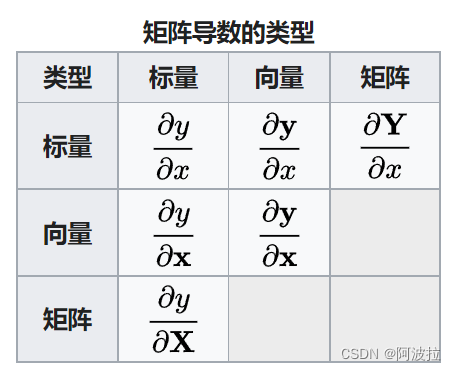
1.求偏导的自变量的符号区别 使用标量、向量和矩阵总共有九种可能性。请注意,当我们考虑每个自变量和因变量中更多数量的分量时,我们可能会留下非常多的可能性。下表收集了最能以矩阵形式最整齐地组织的六种导数。 在这里,我们使用了最一般意义上的术语“矩阵”,认识到向量和标量只是分别具有一列和一行的矩阵。此外,我们使用粗体字母表示向量,使用粗体大写字母表示矩阵。此表示法自始至终使用。 请注意,我们还可