以前看到C++标准上说，移位运算符（<<、>>）出界时的行为并不确定： The behavior is undefined if the right operand is negative, or greater than or equal to the length in bits of the promoted left operand. 我当时也没有深究过这个问题。前几天有个网友来信问

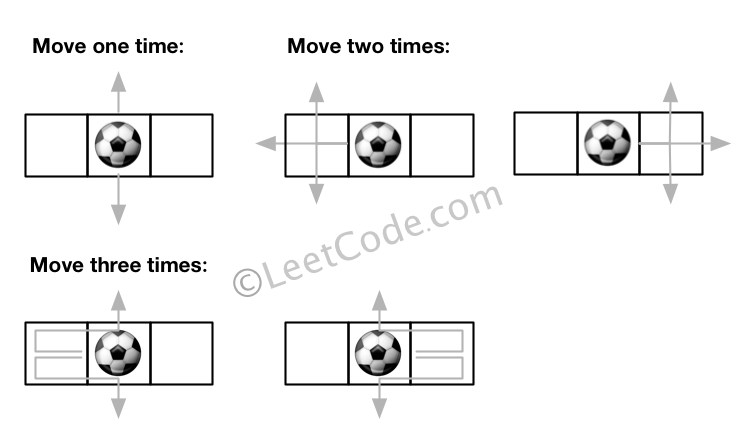
给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。 示例 1： 输入: m = 2, n = 2, N = 2, i = 0, j = 0 输出: 6 解释: 示例 2：

出界的路径数题解集合 记忆化搜索动态规划额外补充--动态规划套壳法 记忆化搜索 递归三部曲: 递归结束条件(base case)：当前位置出界，说明找到一条路径返回值:以当期位置为起点的路径总数本级递归:当前位置的路径和等于来自他四个方向路径之和 const int mod = 1e9 + 7;class Solution {map<pair<pair<int

这道题用普通的dfs和bfs要超时，可以用动态规划或者记忆化搜索解决。 //动态规划算法class Solution {public:int dx[4]={0,0,1,-1};int dy[4]={1,-1,0,0};int countpath=0;int mod=1e9+7;int findPaths(int m, int n, int maxMove, int startRow, i

题解： 动态规划五部曲： 1、确定dp数组及其下标含义 dp[i][j][k]表示球移动i次之后位于坐标(j,k)的路径数，由题意i从0到maxmove遍历，累加出界的路径数即可 2、确定递推式 球移动了i次之后位于坐标(j,k),（不出界且i小于maxmove的情况下）则移动i+1次之后，球必定位于与坐标(j,k)相邻的一个坐标（j1,k1），如果此时球出界了 则将dp[i][j][k]的值加

出界的路径数 给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。     示例 1： 输入: m = 2, n = 2, N = 2, i = 0, j = 0 输出: 6

题目 LeetCode自搜 题解 建议看《忆甜思苦，DFS + 记忆化搜索》，链接： https://leetcode-cn.com/problems/out-of-boundary-paths/solution/yi-tian-si-ku-dfs-ji-yi-hua-sou-suo-by-i-iteo/ 我是看了官方题解自闭后，发现的这个宝藏题解， 如果直接看觉得过于简洁的话，可以先看一遍

题目详情 给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。   示例 1： 输入: m = 2, n = 2, N = 2, i = 0, j = 0输出: 6解释:

Leetcode 576. 出界的路径数 题目 给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。 测试样例 示例 1： 输入: m = 2, n = 2, N = 2,

记忆化dfs 已遍历过的点他的方案数已知晓 所以无需重新遍历 class Solution {int MOD = (int)1e9 + 7;int[][][] dp;int m1,n1,maxstep=0;public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {m1=m;n1=n;maxst