Leetcode 576.出界的路劲数

出界的路径数

给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 10⁹ + 7 的值。

   

示例 1：

输入: m = 2, n = 2, N = 2, i = 0, j = 0

输出: 6

解释:

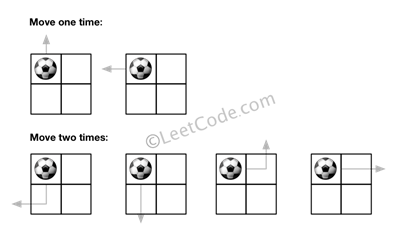
示例 2：

输入: m = 1, n = 3, N = 3, i = 0, j = 1

输出: 12

解释:

   

说明:

1. 球一旦出界，就不能再被移动回网格内。
2. 网格的长度和高度在 [1,50] 的范围内。
3. N 在 [0,50] 的范围内。

思路

以(i, j)为起始点，其中dp[k][x][y]表示用了k步，进入(x, y)位置的路径数，由于dp[k][x][y]只依赖于dp[k-1][x][y]，所以我们可以用一个二维dp数组来代替，初始化dp[i][j]为1，总共N步，进行N次循环，每次都新建一个mxn大小的临时数组t，然后就是对于遍历到的每个位置，都遍历其四个相邻位置，如果相邻位置越界了，那么我们用当前位置的dp值更新结果res，因为此时dp值的意义就是从(i,j)到越界位置的路径数。如果没有，我们将当前位置的dp值赋给t数组的对应位置，这样在遍历完所有的位置时，将数组t整个赋值给dp，然后进入下一步的循环。

 

class Solution {
    public int findPaths(int m, int n, int N, int x, int y) {
        int M=1000000007;
        int[][] dp=new int[m][n];
        int[][] dt={{-1,0},{1,0},{0,-1},{0,1}};
        dp[x][y]=1;
        int res=0;
        for(int k=0;k<N;k++){
            int[][] t=new int[m][n];
            for(int i=0;i<m;i++){
                for(int j=0;j<n;j++){
                    for(int[] d:dt){
                        int r=i+d[0];
                        int c=j+d[1];
                        if(r<0||r>=m||c<0||c>=n)
                            res=(res+dp[i][j])%M;
                        else
                            t[r][c]=(t[r][c]+dp[i][j])%M;
                    }
                }
            }
            dp=t;
        }
        return res;
    }
}