leetcode 576. 出界的路径数

记忆化搜索

递归三部曲:

• 递归结束条件(base case)：当前位置出界，说明找到一条路径
• 返回值:以当期位置为起点的路径总数
• 本级递归:当前位置的路径和等于来自他四个方向路径之和

const int mod = 1e9 + 7;
class Solution {map<pair<pair<int,int>, int>, long> ret;
public:int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {return dfs(m, n, startRow, startColumn,maxMove);}int dfs(int m, int n, int i, int j, int num){//当前位置出界，说明找到一条路径if (i< 0 || j< 0 || i>= m || j>= n)return 1;//判断当前位置的结果是否求出if (ret.find({{ i,j }, num}) != ret.end())return ret[{ {i, j}, num}];//如果当前可移动次数小于等于0，并且还没有出界，那么则不算一条路径if (num<=0)return 0;//当前位置的路径和等于来自他四个方向之和int sum = 0;sum += dfs(m, n, i + 1, j, num - 1);sum %= mod;sum += dfs(m, n, i - 1, j, num - 1);sum %= mod;sum += dfs(m, n, i, j + 1, num - 1);sum %= mod;sum += dfs(m, n, i, j - 1, num - 1);sum %= mod;return ret[{ {i, j}, num}]=sum ;}
};

动态规划

我们可以根据上面的记忆化搜索来写出动态规划，方法如下:

• 首先看记忆化搜索的函数原型:int dfs(int m, int n, int i, int j, int num)
• 其中 m和 n 是对应了题目的源输入，用来表示矩形是几行几列的，整个 DFS 过程都不会发生变化，因此我们无须理会。
• (i,j) 代表当前所在的位置，num 代表最多的移动次数，返回值代表路径数量。
• 重点放在 DFS 函数签名中的「可变参数」与「返回值」。这和我们【动态规划】中的「状态定义」强关联。
• 我们可以设计一个二维数组 f[][]作为我们的 dp 数组：
• 第一维代表 DFS 可变参数中的 (x,y)。取值范围为 [0, m*n)
• 第二维代表 DFS 可变参数中的 num。取值范围为 [0,N]
• dp 数组中存储的就是我们 DFS 的返回值：路径数量。
• 根据 dp 数组中的维度设计和存储目标值，我们可以得知「状态定义」为：
• f[i][j] 代表从位置 i出发，可用步数不超过 j 时的路径数量。
• 状态定义已经得出,接下来需要考虑「转移方程」。
• 当有了「状态定义」之后，我们需要从「最后一步」来推导出「转移方程」：
• 由于题目允许往四个方向进行移动。
• 因此我们的最后一步也要统计四个相邻的方向。
• 举个🌰，假设我们当前位置为(x,y)，而 (x,y) 四个方向的相邻格子均不超出矩形。即有：
• (x,y) 出发的路径数量 = 上方 (x-1,y) 的路径数量 + 下方 (x+1,y)的路径数量 + 左方 (x,y-1) 的路径数量 + 右方 (x,y+1) 的路径数量
• 由此可得我们的状态转移方程：
• f[(x,y)][step]=f[(x−1,y)][step−1]+f[(x+1,y)][step−1]+f[(x,y−1)][step−1]+f[(x,y+1)][step−1]
• 从转移方程中我们发现，更新 f[i][j]依赖于 f[i][j−1]，因此我们转移过程中需要将最大移动步数进行从小到大枚举。
• 至此，我们已经完成求解「路径规划」问题的两大步骤：「状态定义」&「转移方程」。
• 但这还不是所有，我们还需要一些有效值来滚动下去。
• 其实就是需要一些「有效值」作为初始化状态。
• 观察我们的「转移方程」可以发现，整个转移过程是一个累加过程，如果没有一些有效的状态（非零值）进行初始化的话，整个递推过程并没有意义。
• 那么哪些值可以作为成为初始化状态呢？
• 显然，当我们已经位于矩阵边缘的时候，我们可以一步跨出矩阵，这算作一条路径。
• 同时，由于我们能够往四个方向进行移动，因此不同的边缘格子会有不同数量的路径。
  
• 换句话说，我们需要先对边缘格子进行初始化操作，预处理每个边缘格子直接走出矩阵的路径数量。目的是为了我们整个 DP 过程可以有效的递推下去。

class Solution {int mod = (int)1e9+7;int m, n, N;public int findPaths(int _m, int _n, int _N, int _i, int _j) {m = _m; n = _n; N = _N;// f[i][j] 代表从 idx 为 i 的位置出发，移动步数不超过 j 的路径数量int[][] f = new int[m * n][N + 1];// 初始化边缘格子的路径数量for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (i == 0) add(i, j, f);if (i == m - 1) add(i, j, f);if (j == 0) add(i, j, f);if (j == n - 1) add(i, j, f);}}// 定义可移动的四个方向int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};// 从小到大枚举「可移动步数」for (int step = 1; step <= N; step++) {// 枚举所有的「位置」for (int k = 0; k < m * n; k++) {int x = parseIdx(k)[0], y = parseIdx(k)[1];for (int[] d : dirs) {int nx = x + d[0], ny = y + d[1];// 如果位置有「相邻格子」，则「相邻格子」参与状态转移if (nx >= 0 && nx < m && ny >= 0 && ny < n) {f[k][step] += f[getIndex(nx, ny)][step - 1];f[k][step] %= mod;}}}}// 最终结果为从起始点触发，最大移动步数不超 N 的路径数量return f[getIndex(_i, _j)][N];}// 为每个「边缘」格子，添加一条路径void add(int x, int y, int[][] f) {int idx = getIndex(x, y);for (int step = 1; step <= N; step++) {f[idx][step]++;}}// 将 (x, y) 转换为 indexint getIndex(int x, int y) {return x * n + y;}// 将 index 解析回 (x, y)int[] parseIdx(int idx) {return new int[]{idx / n, idx % n};}
} 

额外补充–动态规划套壳法

• 但是上诉求解出边缘格子进行初始化的操作优点繁琐,可否有避免初始化边缘格子的方法呢?
• YES！
• 套壳法，看图:
  
• 外层新增的一圈值都初始化为1，表示一旦出界那么就会得到一条路径

状态定义

• dp[i][j][num]:表示从(i,j)出发第num步出界的路径总数，等价于从外界出发第k步走到(i,j)的路径总数

状态转移

• 显然我们可以直接获得如下状态转移方程

dp[i][j][k] = dp[i-1][j][k-1]+dp[i+1][j][k-1] + dp[i][j-1][k-1]+dp[i][j+1][k-1]

初始化：我们需要注意外界的坐标的初始状态对应的值为1，即

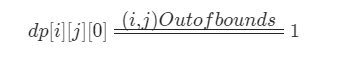
如何求解

• 有了每一个点的每一步对应的值，我们可以说是什么都不怕了
• 题目求的是最多移动N次，出界的路径数，因此我们只需要讲每一步对应的值都加起来即可
• 人话:对每个位置来说，把它从一步出界的路径数量，二步出界的路径数量…num步出界的路径数量累加起来，得到当前位置出界的路径数量总和
  
  

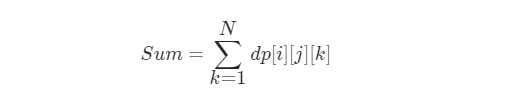
代码展示:

const int mod = 1e9 + 7;
class Solution {
public:int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {//f[i][j][num]从(i,j)出发第num步出界的路径总数，等价于从外界出发第num步走到(i,j)的路径总数vector<vector<vector<int>>> dp(m + 2, vector<vector<int>>(n + 2,vector<int>(maxMove+1,0)));//外部一圈初始化for (int i = 0; i < n + 2; i++)//第一行和最后一行同时进行初始化{dp[0][i][0] = 1;dp[m + 1][i][0] = 1;}for (int j = 1; j < m+2; j++)//左右两列初始化{dp[j][0][0] = 1;dp[j][n + 1][0] = 1;}for (int k = 1; k <= maxMove; k++){for (int i = 1; i < m + 1; i++){for (int j = 1; j < n + 1; j++){dp[i][j][k] += dp[i - 1][j][k - 1];dp[i][j][k] %= mod;dp[i][j][k] += dp[i + 1][j][k - 1];dp[i][j][k] %= mod;dp[i][j][k] += dp[i][j - 1][k - 1];dp[i][j][k] %= mod;dp[i][j][k] += dp[i][j + 1][k - 1];dp[i][j][k] %= mod;}}}//计算起点出界路径总和int sum = 0;for (int k = 1; k <=maxMove; k++){sum=(sum+dp[startRow+1][startColumn+1][k])%mod;}return sum;}
};