576. 出界的路径数(C++)---动态规划解题

题目详情

给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。

示例 1：

输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6
解释:

示例 2：

输入: m = 1, n = 3, N = 3, i = 0, j = 1
输出: 12
解释: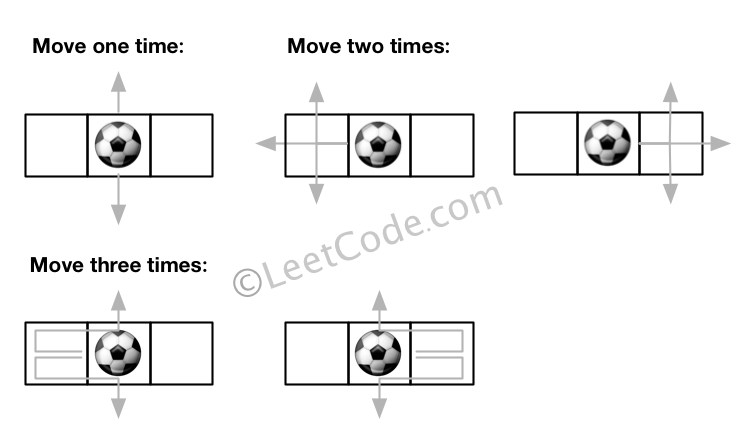

说明:

1. 球一旦出界，就不能再被移动回网格内。
2. 网格的长度和高度在 [1,50] 的范围内。
3. N 在 [0,50] 的范围内。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/out-of-boundary-paths

——题目难度:中等


 

状态dp 解题代码

class Solution {
public:int findPaths(int m, int n, int N, int i, int j) {int mod = 1000000007;vector<vector<vector<unsigned long long>>> dp(m + 2, vector<vector<unsigned long long>>(n + 2, vector<unsigned long long>(N + 1, 0))); //dp[i][j][k] 表示 从坐标(i, j)走k步出界的路径数/*初始化 外界走 0 步(相当于没走)的路径数 为 1 */ for(int i = 0; i < m + 2; i++) {dp[i][0][0] = 1;dp[i][n + 1][0] = 1;}for(int j = 0; j < n + 2; j++) {dp[0][j][0] = 1;dp[m + 1][j][0] = 1;}/*三重for循环*/for(int k = 1; k <= N; k++) {for(int i = 1; i < m + 1; i++) {for(int j = 1; j < n + 1; j++) {dp[i][j][k] = (dp[i - 1][j][k - 1] + dp[i + 1][j][k - 1] +dp[i][j - 1][k - 1] + dp[i][j + 1][k - 1]) % mod;}}}/*统计总路径数*/int ans = 0;for(int k = 1; k <= N; k++) {ans = (ans + dp[i + 1][j + 1][k]) % mod;}return ans;		}
};