公因数专题
最大公因数:欧几里得算法
简述 求两个数字 m和n 的最大公因数,假设r是m%n的余数,只要n不等于0,就一直执行 m=n,n=r 举例 以18和12为例 m n r18 % 12 = 612 % 6 = 06 0所以最大公因数为:6 代码实现 #include<iostream>using namespace std;/
【编程基础C++】素数判定、最小公倍数与最大公因数的实现方法
文章目录 素数法一法二 最大公因数辗转相除法另一写法 最小公倍数直接枚举法根据GCD算LCM 素数 素数 是指大于1的自然数,且只能被1和自身整除。例如,2、3、5和7都是素数。它们在数学中非常重要,因为任何大于1的自然数都可以唯一地表示为素数的乘积,这被称为素数分解。 法一 #include <iostream>using namespace std;bool IsPr
欧几里德算法(求两数最大公因数)
两个整数的最大公因数(gcd)是同时整除两个大最大整数。即gcd(50,15)=5. 算法连续计算余数直到除数为0,最后的非0余数就是最大公因数。因此若M=1989,N=1590,则余数是399,393,6,3,0,从而gcd(1989,1590)=3,这是一个快速算法。 public static long gcd(long m,long n){ while(n !
【一百零五】【算法分析与设计】分解质因数,952. 按公因数计算最大组件大小,204. 计数质数,分解质因数,埃式筛
分解质因数 题目:分解质因数 题目描述 给定一个正整数 n,编写一个程序将其分解为质因数,并按从小到大的顺序输出这些质因数。 输入格式 一个正整数 n,其中 n 的范围是 1 <= n <= 10^18。 输出格式 按从小到大的顺序输出 n 的质因数,每个质因数占一行。 输入示例 4012100 输出示例 2553757 提示 程序需要处理大整数,因此使用 long long 类型。
最大公因数和最小公倍数函数(补续)
大约在去年的时候我发了一篇关于最大公因数和最小公倍数的文章 最小公倍数和最大公约数如何求(函数) 当时我只在里面讲了辗转相除和暴力两种方法,一个O(logn),一个O(n),现在我又带着新的方法回来了(v-v ) 递归 递归的话肯定就是要用递归函数了,我们令gcd(a,b)为a和b 的最大公因数 那么可以写出以下递归式 return gcd(b,a%b); 其原理呢就是辗转相除,那什么时
【并集查找 最大公约数 调和数】952. 按公因数计算最大组件大小
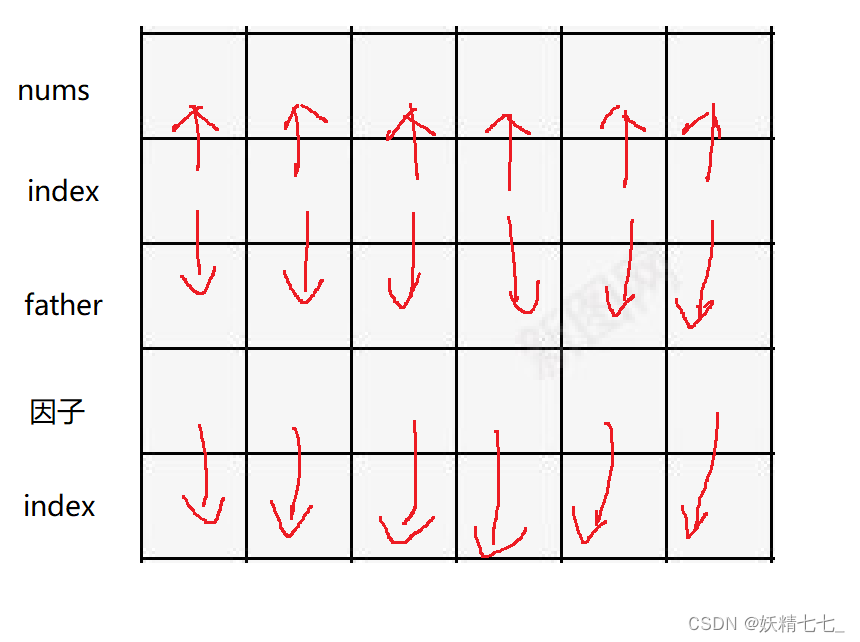
本文涉及知识点 图论 并集查找 最大公约数 调和数 LeetCode952. 按公因数计算最大组件大小 给定一个由不同正整数的组成的非空数组 nums ,考虑下面的图: 有 nums.length 个节点,按从 nums[0] 到 nums[nums.length - 1] 标记; 只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时,nums[i] 和 nums[j]之
C语言求两正整数的最大公因数
思路:辗转相除法 第一种方法: int normal_gcd(int x, int y) {int min,max;if (x >= y)min = y;elsemin = x;while (min != 0) {if ((x%min == 0)&&(y%min==0))return min;else min -= 1;}} 第二种方法: int Euc_rec_
Python实用代码之:如何找两个数的最大公因数?
文章目录 前言1.简单版2.函数封装版 前言 大家好,我是BoBo仔吖,欢迎来看我的文章!这节课,我教大家如何用两种方法输出最大公因数——简单版以及函数版 1.简单版 a = int(input('Enter a number:'))b = int(input('Enter a number:'))t = a % bwhile t != 0:a = bb = tt =
|Python新手小白低级教程|第二十一章:函数(3)【包括使用循环找素数、找两个数的最大公因数、两个数的最小公倍数】
文章目录 上节课答案前言一、for循环之函数封装实战1.封装函数sum_n(a,b),输出a和b之间所有数字的和(包括a,b)2.封装函数prime(min,max),输出1~200间的质数 二、while循环之函数封装实战1.找最大公因数,将函数封装为Common(a,b)2.使用函数Factor(a,b)间接求最小公倍数 总结附: 上节课答案 上节课我留了一道题,大家还记得是
C语言——最大公因数和最小公倍数
在计算机科学中,求解两个或多个数的最大公因数(Greatest Common Divisor,简称GCD)和最小公倍数(Least Common Multiple,简称LCM)是数学计算中的基本问题。C语言作为一种广泛应用于科学计算和工程领域的编程语言,自然也可以用来求解这些问题。本文将详细介绍C语言中求最大公因数和最小公倍数的方法,并附上代码示例。 一、最大公因数 求最大公因数的方法有很多,
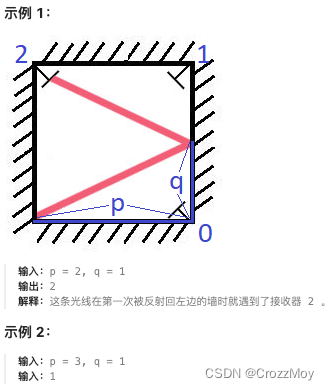
数论Leetcode204. 计数质数、Leetcode858. 镜面反射、Leetcode952. 按公因数计算最大组件大小
Leetcode204. 计数质数 题目 给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。 代码 class Solution:def countPrimes(self, n: int) -> int:if n < 2:return 0prime_arr = [1 for _ in range(n)]prime_arr[0], prime_arr[1] = 0, 0ls = l
求最大公因数的经典算法:Euclid辗转相除法
求两整数最大公约数比较常用,我们可以自定义函数gcd使用: int gcd(int a,int b) { int r; while(b>0) //推荐使用,不必再讨论ab的输入大小情况 { //时间复杂度为
三 求最大公约数(公因数)和最小公倍数
写在前面 求最大公约数和最小公倍数其实是很基础的东西,在刚入门时就会学 这里我想补充一些我从别人那里学到的方法(当然也非常简单,大牛可以不用往下看了) 先看求最大公约数 一 求最大公约数 先看一个无脑的最简单的 简单枚举 思路很简单,我们都知道,n,m(n>m)最大公约数的最大值为m,也就是两数中较小的数,最小值为1 所以我们循环枚举区间(1,m]的数,判断能不能被n和m同时整除 然后我们
最大公因数等于 K 的子数组数目
说在前面 🎈不知道大家对于算法的学习是一个怎样的心态呢?为了面试还是因为兴趣?不管是出于什么原因,算法学习需要持续保持。 题目描述 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 nums 的子数组中元素的最大公因数等于 k 的子数组数目。 子数组 是数组中一个连续的非空序列。 数组的最大公因数 是能整除数组中所有元素的最大整数。 示例 1: 输入:nums =
(3)整除性与最大公因数
整除性 在勾股数组的研究中我们已经看到,整除性与因式分解的概念是数论的重要工具,本节我们将更进一步的考察这些想法。 假设n,m是整数,且m≠0。m整除n指n是m的倍数,即存在k使得n=km。如果m整除n,我们记作m|n。类似的如果m ∤ \nmid ∤n。整除n的都叫n的因数。 最大公因数 两个数a与b(全不为零)的最大公因数就是整除他们两个的最大值,记作 g c d ( a , b )
(3)整除性与最大公因数
整除性 在勾股数组的研究中我们已经看到,整除性与因式分解的概念是数论的重要工具,本节我们将更进一步的考察这些想法。 假设n,m是整数,且m≠0。m整除n指n是m的倍数,即存在k使得n=km。如果m整除n,我们记作m|n。类似的如果m ∤ \nmid ∤n。整除n的都叫n的因数。 最大公因数 两个数a与b(全不为零)的最大公因数就是整除他们两个的最大值,记作 g c d ( a , b )
C语言第二十弹--求最大公因数
求最大公因数 最大公因数:也称最大公约数、最大公因子,指两个或多个整数共有约数中最大的一个。 一、穷举法 思路:找到两个数之间的最少值 使用第三接收最小值,然后通过判断两者%n是否同时等于0,同时为0证明就是两者的最大公因数,不是就n–继续判断。 #define _CRT_SECURE_NO_WARNINGS#include <stdio.h>cint main(){//穷举法int
Algorithm Gossip: 最大公因数、最小公倍数
/**@author 欧阳子木 * Algorithm Gossip: 最大公因数、最小公倍数 * GCD * LCM = 两数乘积 * 设两个数为x和y,其最大公约数为a,则 最小公倍数为(x/a)*(y/a)*a=x *y/a, 最大公约数和最小公倍数的乘积为x *y/a*a=x *y 得证 * @par
34567最大乘积和最小乘积视频_小学数学最大公因数最小公倍数练习,假期练起来!...
往期推荐 【暑期预习】人教版一年级数学上册知识要点 【暑期预习】人教版二年级数学上册知识要点 【暑期预习】人教版三年级数学上册知识要点 【暑期预习】人教版四年级数学上册知识要点 【暑期预习】人教版五年级数学上册知识要点 【暑期预习】人教版六年级数学上册知识要点 五年级数学最大公因数最小公倍数-练习 一、填空。1、把36分解质因数是( ),把60分解质因数是(
【重拾C语言】四、循环程序设计典例整理(最大公因数、阶乘求和、正整数翻译、打印字符方阵、斐波那契数列……)
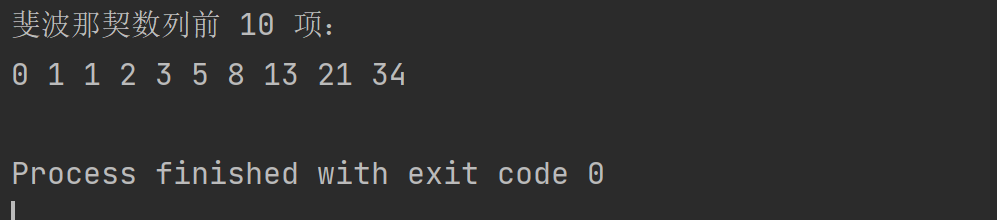
目录 前言 四、循环程序设计 4.3 程序设计实例 4.3.1 求两数最大公因数 4.3.2 阶乘求和 4.3.3 正整数翻译 4.3.4 打印字符方阵 4.3.5 百钱百鸡问题 4.3.6 斐波那契数列 4.3.7 迭代法解方程 前言 ChatGPT C语言是一种通用的、过程式的计算机编程语言,由贝尔实验室的Dennis Ritchie在