互质专题
C++质数的那些事(判断指数、区间筛质数、互质等等)
质数的定义:若一个正整数除了1和它自身之外不能被任何自然数整除,则该数称为质数,也叫素数。否则为合数。 质数的性质:质数的分布较为稀疏,对于一个足够大的数S,不超过S的质数大约有个,也就是说每InN个数约有一个质数, 一、判断一个整数是否是指数 代码: #include<iostream>using namespace std;//判断传入整数是否为质数的自定义函数bool isprim
算法提高之分成互质组
算法提高之分成互质组 核心思想:dfs 枚举每一组可以放哪些元素 #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N = 10;int n;int a[N];int g[N][N];int ans = N;bool st[N];int gcd(int a,int
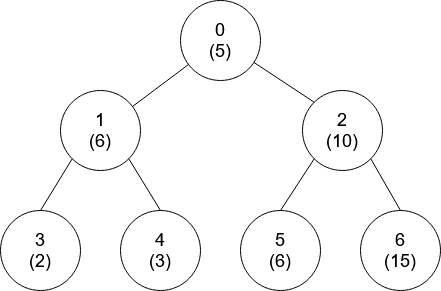
稀碎从零算法笔记Day46-LeetCode:互质树
这几天有点懈怠了 题型:树、DFS、BSF、数学 链接:1766. 互质树 - 力扣(LeetCode) 来源:LeetCode 题目描述 给你一个 n 个节点的树(也就是一个无环连通无向图),节点编号从 0 到 n - 1 ,且恰好有 n - 1 条边,每个节点有一个值。树的 根节点 为 0 号点。 给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i]
分成互质组(dfs)题解
题目描述: 题目分析: 判断题意大体思路是使用dfs进行深度搜索 1、创建一个分组的数组v 2、对每组进行匹配,如果这个深度的数字符合条件,就将其丢进去,然后回溯。 3、如果没有一组能够符合条件,就将这个数字丢进下一组,并新开一组。 代码: #include<bits/stdc++.h>typedef long long ll;using namespace std;int n
深搜+回溯,LeetCode 1766. 互质树
一、题目 1、题目描述 给你一个 n 个节点的树(也就是一个无环连通无向图),节点编号从 0 到 n - 1 ,且恰好有 n - 1 条边,每个节点有一个值。树的 根节点 为 0 号点。 给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值,edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。 当 gcd
欧拉函数确定1-n有多少个数和 n 互质详解 附C语言代码 蓝桥杯互质数的个数
唯一分解定理 任意一个大于 1 的正整数都能被唯一地分解为质因数的乘积。 例如 8 = 2*2*2, 171 = 3*3*19, 30 = 2*3*5, 19 = 19。注意1既不是质数也不是合数。 为什么判断一个数是否是质数只要判断2-√n中有没有因数 24可以分解成 4*6,或者3*8,这两对因数中都是一个小于24的平方根,另一个大于,不可能两个数都小或者两个数都大,因此如果2-√n
hdu 5135 Co-prime(求m以内与n互质的个数)
文章目录 题目链接: 题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=4135 如果是求某一个n互质的个数的话,那确实是这样容斥比较好 原理也感觉比较简单,要找与n互质那就是要找,那就减去不互质的个数不就行了,于是就把n的质因子找出来,那么质因子的倍数就肯定与n不互质,然后就容斥。 容斥有dfs,和位运算枚举出来,而今天学到了一个
poj2891 中国剩余定理不互质
Elina is reading a book written by Rujia Liu, which introduces a strange way to express non-negative integers. The way is described as following: Choose k different positive integers a1, a2, …, ak
容斥原理(有求区间(1-r)里面跟n互质的个数的高效方面模板)
容斥原理 编辑 在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。[1] 中文名 容斥原理 外文名 Principle of inclusion-exclusion[2
中国剩余定理模板(互质与非互质)
互质 #include<bits/stdc++.h>using namespace std;int exgcd(int a,int b,int &x,int &y){if(b==0){x=1,y=0;return a;}int d=exgcd(b,a%b,y,x);y-=a/b*x;return d;}int Chinese_Remainder(int mod[],int prime[
欧拉函数求与N互质的数总个数
欧拉函数的定义 1∼N1∼N 中与 NN 互质的数的个数被称为欧拉函数,记为 ϕ(N)ϕ(N)。 若在算数基本定理中,N=pa11pa22…pammN=p1a1p2a2…pmam,则: ϕ(N)ϕ(N) = N×p1−1p1×p2−1p2×…×pm−1pm 代码: #include<iostream>using namespace std;int n;int main(){sca
证明任意两个自然数互质的概率为6/pi^2
证明任意两个自然数互质的概率为 6 π 2 \frac{6}{\pi^2} π26 设事件 A : { ′ m , n 互 质 ′ } A:\{'m,n互质'\} A:{′m,n互质′},事件 B : { ′ a , b 互 质 ′ } B:\{'a,b互质'\} B:{′a,b互质′},事件 C k : { ′ k 是 a , b 的 公 因 数 ′ } C_k:\{'k是a,b的公因数
中国剩余定理(CRT) 证明 互质与不互质
中国剩余定理(CRT) 图来自博客:https://blog.csdn.net/u012717411/article/details/43168405 我对此做一些解释。 首先,(Mi,mi)=1表示它两互质 下面这个方程更有利于理解扩展欧几里德如何求解 是Mi模mi的逆元, 另一种好理解证明: 代码模板: typedef long long ll;void e
题目52:输入两个正整数m和n,判断m和n是否互质(即最大公约数为1),是则输出Yes,否则输出No。
题目转载:http://python.wzms.com/s/1/53 题目描述: 输入两个正整数m和n,判断m和n是否互质(即最大公约数为1),是则输出Yes,否则输出No。 输入格式: 输入两个整数m和n,中间用空格隔开。 输出格式: 如互质输出Yes,否则输出No。 互质: 互质是公约数只有1的两个整数,叫做互质整数。公约数只有1的两个自然数,叫做互质自然数。后者是前者的特
知识点补充----什么是互质?
什么是互质? 互质是公约数只有1的两个整数,叫做互质整数。公约数只有1的两个自然数,叫做互质自然数,后者是前者的特殊情形。 备注 今天在学习一个算法的时候突然发现了这个词,然后一查发现这个东东竟然是小学数学教材里面的知识点,果然高考后学的东西都还给老师了。日常愧疚+1